Pergunte ao Mago #168

Uma aposta paralela cada vez mais comum que tenho visto em jogos de Texas Hold'em é a aposta no "valor" total do flop, onde o valor de uma carta é atribuído pelas regras do Blackjack (ou seja, A=11, KQJ10=10, as demais são as cartas com valor nominal). Os jogadores têm a opção de escolher um ou mais valores totais, colocando uma aposta paralela no pote. O jogo continua até que o flop atinja um valor que seja coberto por um jogador (portanto, um flop KK4 enviaria o pote para um jogador que apostou em 24). Matematicamente, qual é o melhor número para apostar? Na maioria dos jogos que joguei, há a estipulação de que não se pode apostar em 30, o que levaria a pensar que seria o "melhor" número para apostar, mas considerando que 30 tem um número muito limitado de combinações possíveis (três cartas de valor 10, A-9-10 ou AA-8), não tenho certeza se isso é verdade. Além disso, mãos em que mais jogadores têm cartas de valor dez e ases têm maior probabilidade de ver o flop. Você teria interesse em fazer uma análise dessa aposta paralela?

Scott de Philadelphia

Vou assumir que, se ninguém ganhar no flop, as apostas são reembolsadas ou o próximo flop é usado para resolvê-las, em vez de usar as cartas do turn e do river. Vou ignorar a regra de que, se todos desistirem, a aposta não é resolvida. Claramente, essa regra ajuda os totais mais baixos, mas considerá-la na análise a tornaria complicada e subjetiva. Dito isso, a tabela abaixo mostra a probabilidade de cada total. Como você pode ver, a melhor aposta seria em um total de 23, com uma probabilidade de 8,3982%.

Pontos de Blackjack no Flop

Total	Combinações	Probabilidade
33	4	0,000181
32	96	0,004344
31	504	0,022805
30	840	0,038009
29	784	0,035475
28	920	0,041629
27	1108	0,050136
26	1264	0,057195
25	1472	0,066606
24	1652	0,074751
23	1856	0,083982
22	1800	0,081448
21	1508	0,068235
20	1408	0,06371
19	1336	0,060452
18	1196	0,054118
17	1080	0,048869
16	896	0,040543
15	740	0,033484
14	512	0,023167
13	352	0,015928
12	268	0,012127
11	200	0,00905
10	136	0,006154
9	92	0,004163
8	48	0,002172
7	24	0,001086
6	4	0,000181

Eu trabalho em um cassino e tenho uma aposta de que um crupiê de roleta não pode influenciar o resultado de uma jogada. Certamente há quem acredite que isso seja possível. Não em um número específico, é claro, mas talvez em uma parte da roleta. Qual seria um bom teste para determinar, de forma razoável, se um crupiê influenciou os resultados? Supondo que o número de tentativas seja razoável, compartilharei os resultados com prazer.

Mark S de Sault Ste. Marie

Estou do seu lado. Se isso fosse possível, os crupiês poderiam facilmente conspirar com os jogadores e dividir os lucros. No entanto, nunca ouvi falar disso acontecer. Um bom teste seria pegar alguém que afirma ser capaz de influenciar o resultado dos lançamentos e pedir que essa pessoa tente acertar um número específico em uma das metades da roleta o máximo de vezes possível ao longo de 100 giros. Quanto mais vezes ela conseguir, maior será o peso da sua afirmação. A tabela abaixo mostra a probabilidade de 50 a 70 giros bem-sucedidos. Por exemplo, a probabilidade de 60 ou mais giros bem-sucedidos é de 2,8444%. Limiares de confiança comuns em estatística são os níveis de 90%, 95% e 99%. Para superar um teste de confiança de 90%, no qual a probabilidade de falha em giros aleatórios é de 90%, o número de giros bem-sucedidos precisaria ser de 57 ou mais. Para superar um teste de 95%, o número precisaria ser de 59 ou mais, e em 99%, o número precisaria ser de 63 ou mais.

Probabilidade de pelo menos 50 a 70 giros bem-sucedidos na roleta.

Vitórias	Probabilidade
70	0,000039
69	0,000092
68	0,000204
67	0,000437
66	0,000895
65	0,001759
64	0,003319
63	0,006016
62	0,010489
61	0,0176
60	0,028444
59	0,044313
58	0,066605
57	0,096674
56	0,135627
55	0,184101
54	0,242059
53	0,30865
52	0,382177
51	0,460205
50	0,539795

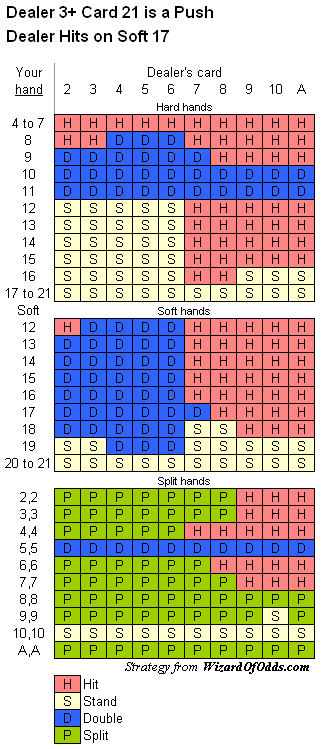
Em Reno, há um novo tipo de promoção de EV positivo. O dealer força todos os "dealer draws para 21". Os dealers com cartas naturais ainda ganham. (Alguma sugestão de estratégia? Os limites da mesa são de $5 a $25, eu sempre jogo o máximo. O jogo básico é H17 DAS RSA com 6 baralhos até 4 mãos.)

Bob de Novato

Uau! De acordo com meus cálculos, isso resulta em uma vantagem de 6,4% para o jogador. Estou supondo que a regra se aplica após dobrar e dividir. Aqui está a estratégia básica para essa regra.

Não consegui encontrar uma tabela de risco de ruína para pôquer pick 'em com pagamento integral, nem informações relacionadas à sua variância. As máquinas de $1 com pagamento integral claramente têm os melhores retornos na região de Buffalo-Niagara, mas não tenho certeza sobre os valores de banca recomendados. Qualquer conselho será muito apreciado. Obrigado.

Fred de Buffalo

O desvio padrão no Pick 'em Poker é de 3,87. O desvio padrão no vídeo poker convencional tende a variar de 4,4 a 6,4. Não tenho tabelas com risco de ruína para o Pick 'em Poker. Portanto, o melhor conselho que posso oferecer é usar a mesa de Jacks or Better no meu apêndice 1 de vídeo poker . Jacks or Better tem o menor desvio padrão nesse apêndice, com 4,42, então você pode ser um pouco mais agressivo do que o recomendado para essa mesa.

Nas minhas partidas caseiras, os jogadores costumam usar vários curingas diferentes. Geralmente, há dois curingas (no beisebol, seguir a dama onde tanto a dama quanto a próxima carta são curingas, no futebol americano) e, ocasionalmente, apenas um (nossa versão de 3-5-7, seguir a dama com apenas a próxima carta como curinga). Nessas partidas com 4 a 8 curingas em potencial, qual é estatisticamente menos provável: uma quina ou uma sequência de flush? Há uma discussão constante sobre isso e eu adoraria que uma fonte respeitável e universalmente reconhecida como você resolvesse a questão. Agradeço antecipadamente.

Myles de Valencia

A probabilidade de uma quina é menor. Acabei de adicionar uma tabela à minha seção sobre probabilidades no pôquer, detalhando a probabilidade de cada mão de acordo com a classificação de cada carta como curinga.

Olá, Wiz. Primeiro, adorei o site. Você está me transformando em um jogador de Blackjack espanhol. Minha esposa e eu jogamos em Laughlin uma vez durante uma viagem a Las Vegas. Gostei do ambiente. Por que não consigo encontrar bons sites sobre Laughlin? Jogamos Blackjack, Blackjack espanhol e Craps. Vamos para Nevada em setembro e gostaríamos de aproveitar melhor nosso orçamento de jogos. Onde você joga quando está no river?

Wavy de Danbury, CT

Quando estou em Laughlin, prefiro o Harrah's. Embora seja também o mais caro na minha opinião, vale a pena o custo extra. Acho o serviço em todos os outros cassinos lento e ruim, e a idade média da clientela é de cerca de 65 anos. No entanto, quando me apetece algo menos corporativo e sofisticado, vou ao Riverside, o único cassino familiar da cidade.