Roleta - Perguntas frequentes
Como você se sairia se jogasse roleta assim: apostando $5 no 0 e no 00, e $15 em duas das colunas? Você não teria cerca de 70% de chance de ganhar?
Você teria 2/38 de chance de ganhar $140, 24/38 de chance de ganhar $5 e 12/38 de chance de perder $40. O retorno esperado total é [(2/38)*140 + (24/38)*5 + (12/38)*-40]/40 = -5,26%. A mesma vantagem da casa que em todas as apostas na roleta com duplo zero (exceto a combinação 0-00-1-2-3, que é de 7,89%).
Suponha que eu entrasse em um cassino e fizesse uma aposta em duas das combinações de pagamento 2 para 1 na roleta, como por exemplo, US$ 100 em 1-12 e US$ 100 em 13-24. Em uma aposta única, minhas chances de levar para casa US$ 100 não seriam de generosos 63%? Não estou falando a longo prazo; apenas de uma aposta única.
Você está certo, as chances de ganhar são de 24/38, ou cerca de 63%. No entanto, você precisa arriscar US$ 200 para ganhar apenas US$ 100. Se quiser aumentar ainda mais suas chances de ganhar, aposte em quaisquer 35 números. A probabilidade de ganhar será de 92%.
Existe alguma maneira de combinar apostas na roleta para maximizar as chances de ganhar? Por exemplo, uma aposta em uma dúzia paga 2 para 1. Se eu fizer duas apostas em dúzias, digamos, no primeiro e no segundo conjunto de 12, tenho 63,16% de chance de ganhar. Essas são probabilidades melhores do que uma simples aposta em vermelho/preto, par/ímpar ou alto/baixo. Embora eu ganhe apenas 1 para 1 em vez de 2 para 1 (se eu ganhar, já que parte da minha aposta tem que ser perdida, pois o número vencedor não pode estar no primeiro e no segundo conjunto de 12), as probabilidades foram ligeiramente alteradas a meu favor ao combinar duas apostas. As probabilidades para esse tipo de combinação já foram determinadas? Se sim, onde posso encontrá-las?
Contanto que você evite a combinação 0-00-1-2-3, a vantagem da casa em qualquer combinação de apostas é sempre exatamente 1/19, ou 5,26%. Existem maneiras de aumentar sua probabilidade de ganhar, mas ao custo de ganhar menos em relação ao valor total apostado.
Eu estava jogando roleta ontem à noite usando o método "Martingale", dobrando a aposta duas vezes após a primeira perda. Uma estratégia idiota, eu sei, mas geralmente não perco muito e jogo há bastante tempo. Enfim, o que acabou com a minha partida foi que eu estava apostando no mesmo valor (ou no valor da aposta) e, em quatro lançamentos, o número 9 saiu em três deles. Qual a probabilidade disso? Parece suspeito? Aliás, será que algum cassino já foi pego trapaceando?
A probabilidade de obter qualquer número três vezes em 4 é 38*4*(1/38) 3 *(37/38) = 1/5932. No entanto, se você jogar por tempo suficiente, é quase impossível não notar eventos incomuns como esse. Isso não chega nem perto de ser suspeito. Trapaças acontecem em cassinos físicos. Geralmente, é um crupiê desonesto que é pego pela segurança do cassino. Houve alguns casos graves de trapaça contra cassinos online, mas, até onde eu sei, nenhuma autoridade governamental jamais condenou alguém.
Não seria uma estratégia ainda pior na roleta apostar em vários números internos em uma única aposta (como a maioria dos jogadores faz) em vez de fazer uma sequência de apostas independentes em um único número? Por exemplo, se alguém tivesse R$ 100, apostar R$ 10 no número "8" dez vezes resultaria em uma perda menor do que apostar R$ 10 em dez números diferentes em uma única rodada? Parece-me que "cobrir" apenas garante que certas apostas (no caso acima, nove apostas) SEMPRE serão perdedoras? Você não aborda o conceito de "cobrir" na sua página?
Veja meus Dez Mandamentos do Jogo . O sexto mandamento é "nunca faça apostas seguras". Sobre sua pergunta sobre roleta, a probabilidade de perder todas as dez apostas apostando uma de cada vez é (37/38) 10 = 76,59%. A probabilidade de perder todas as dez apostas apostando todas de uma vez em números diferentes é (28/38) = 73,68%. Ao fazer apostas seguras, ou seja, apostar em dez números de uma vez, você diminui a probabilidade de uma perda total, mas também limita seu ganho máximo a US$ 26. O jogador que aposta uma de cada vez pode ganhar até US$ 350. Ambos os métodos têm o mesmo retorno total esperado de 94,74%.
Li sua página sobre sistemas e venho falando disso para as pessoas há anos! Trabalho como crupiê de roleta em um cassino e já vi todos os sistemas possíveis em algum momento. Vi um sistema que, embora possa não funcionar em uma simulação de computador (e provavelmente não funcionará), "parece" funcionar na vida real. Isso significa que o vi ganhar mais do que perder.
Funciona assim: o jogador aposta 75 dólares nos números de 1 a 18, 50 dólares no terceiro número (12) e 10 dólares na aposta combinada de 0 a 00, totalizando 135 dólares. Isso cobre todos os números, exceto seis (de 19 a 22), e rende um pagamento de 15 dólares cada vez que a bola erra esses seis números, EXCETO quando sai 0 ou 00, caso em que o pagamento é de 40 dólares. Eu sei que parece loucura!!! Mas acredite, eu vi esse sistema ganhar mais do que perder. Ele também funciona ao contrário (óbvio). Eu adoraria saber as probabilidades reais desse sistema, mas é difícil dizer para alguém que não funciona quando essa pessoa sai da minha mesa com 2 mil dólares a mais no bolso :-)
Existem 30 maneiras de ganhar $15, 6 maneiras de perder $135 e 2 maneiras de ganhar $45 (e não $40). O retorno esperado dessa combinação de apostas é ((30/38)*15 + (6/38)*-135 + (2/38)*(45))/135 = -0,0526, ou 5,26%, a vantagem da casa em qualquer aposta individual ou combinação de apostas, desde que a temida combinação 0-00-1-2-3 seja evitada. Em suas observações, você provavelmente viu menos ocorrências do que o esperado (entre 19 e 24), o que explica a ilusão de que esse método é vencedor.
Olá, Mago, eu estava pensando sobre roleta. Com o software da Boss Media, você pode girar a roleta sem fazer uma aposta. Isso não seria vantajoso para o jogador? Em alguns sistemas de apostas na roleta que eu já vi, como o Martingale, você dobra a aposta quando perde, por exemplo. Não seria possível simplesmente observar a roleta sem apostar e, com base nas rodadas anteriores, fazer a sua aposta? Por exemplo, girar a roleta 5 vezes antes de fazer uma aposta. Suponha que todos os números sejam ímpares. Não faria sentido começar a apostar no par? Eu sei que isso meio que se baseia na falácia do apostador e que a roleta não se importa com o resultado da última rodada, mas a probabilidade de sair um número ímpar diminui a cada rodada. Estou no caminho certo ou apenas repetindo uma teoria antiga?
Você está apenas repetindo a falácia do apostador. Se a bola cair no número ímpar 100 vezes seguidas em uma roleta honesta, a probabilidade de a próxima rodada ser par continua a mesma de todas as rodadas, 47,37% em uma roleta com duplo zero. Portanto, não adianta nada poder girar a roleta sem apostar. A bola não tem memória.
Embora a roleta claramente não possa ser vencida pela sorte, ouvi dizer que é possível vencê-la pelas leis da física de duas maneiras (em teoria). Primeira maneira: um dispositivo de alta tecnologia que mede a velocidade da bola em relação à velocidade da roleta e prevê o setor de resultado com cerca de 40% de precisão. Segunda maneira: viés na roleta. Obviamente, uma roleta teria que ter um viés de pelo menos 5,26% para que o jogador tivesse chances iguais. A questão é: quantas rodadas, você diria, mago, seriam necessárias para determinar o viés da roleta, se é que existe algum?
Já ouvi falar do uso dessas duas técnicas. Não sei muito sobre dispositivos para manipular roletas, exceto que se sabe que existem e são usados de vez em quando. Aqui em Nevada, um dispositivo desses seria totalmente ilegal. Já sobre tirar proveito de roletas viciadas, ouço falar muito mais. Isso já aconteceu várias vezes. Acho que cassinos com roletas antigas são os alvos mais vulneráveis. Há anos venho dizendo que a Argentina é um alvo perfeito para isso.
Ao jogar o sistema Martingale de duplicação contra a roleta de zero único em qualquer uma das probabilidades iguais, calculei que você perderá uma vez a cada 248 sessões. Isso significa uma sessão que termina com um ganho de uma unidade ou uma perda de 255 unidades. Meu cálculo está correto? Caso contrário, poderia me informar as probabilidades corretas?
Se a perda máxima for de 255 unidades, você pode apostar até 8 vezes. A probabilidade de perder oito apostas seguidas é (19/37) 8 = 0,004835. Portanto, você tem 99,52% de chance de ganhar uma unidade e 0,48% de chance de perder 255 unidades.
Em média, na roleta de zero único, com que frequência um número se repete (ex.: dois 8 seguidos) ao longo de 36 rodadas?
Você pode esperar uma repetição a cada 37 pares de números. Portanto, com 36 números, temos 35 pares de números. Assim, o número esperado de repetições é 35/37 = 0,9459.
Todo mundo diz que não se pode vencer a roleta a longo prazo com sistemas matemáticos. Mas como explicar o fato de existirem jogadores profissionais que ganham a vida jogando roleta? Acho que não é só exibicionismo. Eles realmente ganham mais do que perdem jogando no dia a dia.
Mostre-me alguém que ganha em um jogo justo de roleta e eu lhe mostrarei alguém que apenas teve sorte e provavelmente perderá tudo. Só é possível vencer na roleta com habilidade, jogando com vantagem, como explorar uma roleta viciada ou usar técnicas de manipulação de resultados.
Li tudo o que você escreveu sobre roleta, mas não encontrei nada sobre os operadores de roleta. Sob o olhar atento do gerente de mesa, o operador de roleta lança "seções" para melhorar as probabilidades da casa. O operador que consegue lançar números verdes, não sempre, mas com uma boa porcentagem de vezes, talvez uma em cada 7 ou 8, quando quer eliminar um grande prêmio acumulado, aposta.
Os cassinos não precisam recorrer a essas táticas para ganhar. Além disso, os cassinos não têm nada a temer dos apostadores de jackpot progressivo. Na maioria das vezes, os apostadores de jackpot progressivo ganham, mas os poucos que atingem seus limites de banca pagam por todos os vencedores e ainda sobra para o cassino. Além disso, seria necessário muita habilidade para girar deliberadamente uma bola em uma seção específica. Não acredito que isso possa ser feito com qualquer grau significativo de precisão.
Olá Wizard, seu site é ótimo. Na roleta com duplo zero, percebo que todas as apostas têm a mesma alta vantagem da casa, mas estou terminando um curso de estatística e me parece que nem todas as apostas são exatamente iguais devido aos seus desvios padrão. Uma aposta de $1 no vermelho, por exemplo, tem um desvio padrão de 1,012019, enquanto uma aposta de $1 em um único número tem um desvio padrão de 5,839971, de acordo com meus cálculos. Assim, a probabilidade esperada de sair vencedor em 1, 100 e 10.000 tentativas, respectivamente, é de 0,4793, 0,3015 e 0,0000 para uma aposta com probabilidade igual (1/1), e de 0,4964, 0,4641 e 0,1837 para uma aposta em um único número. Minha análise está correta? (Assumi normalidade) Obrigado!
Obrigado pelo elogio. Primeiramente, o desvio padrão em qualquer aposta com odds iguais é 0,998614 e em uma aposta em um único número é 5,762617. A probabilidade de sair vencedor apostando em odds iguais em 1, 100 e 10.000 rodadas é de 0,473684, 0,265023 e 0,00000007, respectivamente. A probabilidade de sair vencedor apostando em um único número em 1, 100 e 10.000 rodadas é de 0,0263158, 0,491567 e 0,18053280, respectivamente. Parece que você está tentando argumentar que as apostas em um único número são melhores devido à maior probabilidade de terminar com lucro em comparação com apostas múltiplas. Isso é verdade, porém a probabilidade de uma perda substancial também é muito maior. Ao longo de uma sessão, os resultados esperados sempre se situam em algum ponto de uma curva normal. Em apostas de baixa volatilidade, como vermelho ou preto, a curva normal é acentuada e não se desvia muito de uma pequena perda. Já em apostas de alta volatilidade, como números individuais, a curva normal é ampla, permitindo uma gama muito maior de resultados líquidos, tanto positivos quanto negativos.
Meu colega D. insiste que aperfeiçoou um método para ganhar sempre na roleta. Não estou convencido. Será que ele só tem sorte ou existe algum sistema que funciona?
Ele só tem sorte. Como já disse milhares de vezes, nenhum sistema de apostas resiste ao teste do tempo.
Li seu tópico sobre o método Martingale na seção de Roleta. Tentei esse método algumas vezes no computador e cheguei a ganhar US$ 500. Depois fui ao cassino e perdi mais de US$ 1000, porque o preto saiu oito vezes seguidas. Mas estou começando a aprender bacará. Estava tentando no computador e, novamente, ganhei US$ 500 apostando no banqueiro. Comecei com US$ 20, depois fui para US$ 40, depois US$ 80 e assim por diante. Consegui um lucro de US$ 500 mesmo pagando os 5% em cada mão. Você acha que esse método funcionaria em um cassino? Pensei em perguntar antes de ir e perder outros US$ 1000. Como eu disse, o preto saiu oito vezes seguidas. Mas você acha que a mão do jogador ganharia oito vezes seguidas? Além disso, este jogo é bom porque um empate é considerado um push, enquanto na roleta, 0 (ou 00) significa derrota.
A estratégia Martingale é perigosa em todos os jogos e, a longo prazo, nunca será vencedora. No entanto, é melhor usá-la no bacará do que na roleta, devido à menor vantagem da casa. A probabilidade de um jogador ganhar 8 vezes seguidas é de 0,493163^8 = 1 em 286. Além disso, lembre-se de que você pode ganhar uma mão no final da sequência e ainda assim sair no prejuízo por causa da comissão. Por exemplo, se você começou com uma aposta de $1 e ganhou na 7ª mão, você ganharia $60,80 ($64 * 95%), o que não cobriria os $63 em perdas anteriores.
Olá. Você disse que todos os sistemas de apostas falharão. Se você jogar roleta e apostar uma unidade nos números de 1 a 12 e duas unidades nos números de 13 a 24, você não teria então 66,66% de chance de empatar ou ganhar?
Não exatamente. Você teria 12/38 de chance de ganhar 3 unidades, 12/38 de não ter prejuízo e 14/38 de perder 3 unidades. O valor esperado é [(12/38)*3 + (12/38)*0 + (14/38)*-3]/3 = (-6/38)/3 = -2/38 = -5,26%. Isso será válido para qualquer combinação de apostas, desde que você evite a temida combinação de 5 números (0/00/1/2/3). Se você jogar apenas uma rodada e quiser maximizar sua probabilidade de ganhar, aposte igualmente em 35 dos números. Você terá 92,11% de chance de ganhar 1 unidade e 7,89% de chance de perder 35 unidades.
Olá. Sou um ávido jogador de roleta há alguns anos e, pela primeira vez, estou pensando em experimentar um sistema de roleta... Sei como você se sente em relação a esses tais "sistemas" e aos golpistas por trás deles, e acredite, eu me sinto da mesma forma, mas encontrei dois sistemas que não podem ser ignorados...
A primeira é a estratégia 3q/A encontrada no livro "Gamble to Win: Roulette", de RD Ellison, que possui uma taxa de sucesso comprovada de 7,94% (7500 rodadas). O sistema foi testado e desenvolvido em conjunto com "Spin Roulette Gold", de Frank Scoblete, e "Roulette System Tester", de Eric St. Germain.
O segundo é o sistema de roleta de Don Young, que comprovadamente supera o testador de sistemas de roleta da Zumma Publishing (15.000 giros).
Devo dizer que ainda estou um pouco cético em relação a gastar dinheiro nesses sistemas, mas como eles já provaram seu valor a longo prazo, não vejo motivo para não fazê-lo. Afinal, superar esses livros de questões deve significar alguma coisa...
Qual a sua opinião sobre esses sistemas? E você acha que eu deveria experimentá-los?
Muito obrigado! Tenha um ótimo dia. Tudo de bom!
7500 rodadas? Só isso? Qualquer um pode obter um lucro de 7,94% do total apostado em 7500 rodadas se jogar agressivamente. O mesmo vale para 15000 rodadas. A maioria dos sistemas é projetada para ter muitas vitórias pequenas e poucas derrotas grandes. Um sistema que exige uma banca enorme pode facilmente chegar a 15000 rodadas e mostrar lucro. Eventualmente, as perdas virão e ele não resistirá ao teste do tempo. As grandes perdas também podem ocorrer no início. A verdadeira maneira de testar um sistema é jogá-lo bilhões de vezes. Minha opinião sobre esses sistemas é a mesma que sobre todos os outros: eles não valem nada. Não tenho problema nenhum em você experimentá-los, mas tenho problema nenhum com qualquer pessoa que coloque um centavo sequer no bolso de quem os vende.
Nota: Veja a continuação desta pergunta na próxima coluna .
Prezado Senhor, em um jogo de roleta com um único zero, a PROBABILIDADE de ganhar aumenta se você apostar uma parte do seu dinheiro em menos números por mais rodadas, em vez de cobrir mais números por rodada. Por exemplo: se você estiver disposto a arriscar US$ 500 para ganhar US$ 250, você poderia: Opção (A): apostar US$ 250 em qualquer uma das duas dúzias e, caso ganhe, receberá US$ 250. A probabilidade disso acontecer é de 24/37 = (0,648648). Opção (B): apostar US$ 125 em qualquer uma das dúzias e, caso ganhe, receberá US$ 250 e encerrará o jogo. No entanto, caso perca, você poderá apostar US$ 187,50 na mesma dúzia e, caso ganhe, receberá US$ 375, o que lhe dará os US$ 250 e os US$ 125 perdidos na rodada anterior. Mesmo que você perca nas duas rodadas, ainda terá US$ 187,50 para jogar e poderá apostar US$ 20,833333 em quaisquer nove números. Se você ganhar, receberá US$ 750, o que equivale ao seu capital inicial de US$ 500 mais US$ 250 de prêmio, que era o seu objetivo. A probabilidade de isso acontecer, ou seja, acertar pelo menos uma dúzia OU nove números uma vez em três rodadas, é igual a [1-(25/37)x(25/37)x(28/37)]=0,65451. Portanto, com o MESMO capital e o MESMO retorno, você pode aumentar sua PROBABILIDADE de sucesso, como na opção (B), se jogar com menos números e menos dinheiro, mas TALVEZ por mais rodadas (já que você pode ganhar na primeira rodada). Você pode até melhorar ainda mais sua probabilidade se jogar apenas seis números por vez e tentar ganhar US$ 250. Alguma explicação? Assegurando-lhe os meus mais sinceros agradecimentos e aguardando a sua resposta, permaneço à disposição.
Você está correto ao afirmar que a opção B tem maior probabilidade de sucesso, embora o objetivo e o capital sejam os mesmos. A razão é que o valor médio apostado na opção B é menor, portanto seu dinheiro fica menos exposto à vantagem da casa, aumentando assim a probabilidade de ganhar. O valor apostado na opção A é sempre de $500. O valor médio apostado na opção B é (12/37)*125 + (25/37)*(12/37)*(125+187,5)+ (25/37)*(25/37)*(125+187,5+187,5) = 337,29.
Quando participei do Vegas Challenge, faltando poucos minutos para o fim, eu tinha cerca de US$ 8.000 e precisava chegar a pelo menos US$ 24.000. Então, dividi meu saldo em quatro partes de US$ 2.000 cada e apostei cada uma em uma combinação de 4 números, cada uma das quais pagaria US$ 22.000. Dessa forma, eu não estava necessariamente expondo toda a minha aposta à vantagem da casa, o que aumentou minha probabilidade de ganhar.
Apostar em todos os 38 números da roleta tornaria impossível vencer as probabilidades, mesmo por um curto período, e com uma aposta de US$ 1 por número, haveria uma perda de US$ 2 por giro da roleta (roleta 0, 00, sem regras vantajosas para apostas com probabilidades iguais). Seria razoável que houvesse um intervalo ideal de números para apostar com base em estatísticas?
Eu avalio o valor de uma aposta pelo retorno esperado, não pela probabilidade de ganhar. Portanto, apostar em todos os 38 números tem uma vantagem da casa de 2/38 = 5,26%, a mesma que apostar em um único número ou em qualquer número de números cobertos. Embora apostar em todos os 38 números tenha 0% de chance de resultar em um lucro líquido, a desvantagem é perder apenas 5,26% do total apostado. Se você for obrigado a apostar e quiser minimizar a variância, então deve apostar em todos os 38 números. Um exemplo prático seria se você tivesse fichas promocionais que precisasse apostar e não quisesse arriscar, mas sim obter o valor esperado exato delas. Então, para responder à sua pergunta, não existe um intervalo ideal de números. Todos os intervalos têm o mesmo valor esperado.
Hoje circulou uma história sobre um britânico que apostou todas as suas economias em uma única jogada de roleta. Meu amigo e eu estávamos debatendo sobre qual seria a melhor aposta em um cassino para esse tipo de situação. Se você só pode fazer uma aposta e quer maximizar suas chances, qual o melhor jogo para jogar e qual a melhor aposta?
Primeiro, preciso dizer que esse cara foi um tolo. Ele apostou US$ 138.000 em uma roleta americana normal, que tem dois zeros e uma vantagem da casa de 5,26%. Isso resultou em uma perda esperada de US$ 7.263. No entanto, se ele tivesse feito um trajeto de 10 minutos até o Bellagio, o Mirage ou o Aladdin, poderia ter feito a aposta em uma roleta com um único zero, que segue a regra europeia de devolver metade da aposta (com odds iguais) se a bola cair no zero. De qualquer forma, ele planejava fazer uma aposta com odds iguais. Portanto, nessas roletas com as regras europeias completas, a vantagem da casa teria sido de apenas 1,35%, resultando em uma perda esperada de apenas US$ 1.865.
Para responder à sua pergunta, se fosse obrigado a fazer apenas uma aposta com probabilidades iguais, eu teria escolhido a aposta no banqueiro no bacará, com uma vantagem da casa de 1,06%.
Qual é o meu risco de ruína com o seguinte padrão de apostas na roleta?
Questões sobre risco de ruína são matematicamente complexas. A menos que seja um jogo simples de ganhar/perder, eu recomendaria fazer uma simulação aleatória em um computador.
Moro em Nova Jersey, a cerca de duas horas ao norte de Atlantic City. Você sabe onde fica a roleta europeia mais próxima de alguém na minha região?
Existem muitas máquinas caça-níqueis com um único zero em Atlantic City. A maioria dos cassinos de lá as possui, mas com uma aposta mínima de US$ 25.
Eu estava no Casino On Net jogando roleta. Fiz apostas seguras, apostando apenas no primeiro 12 (L), segundo 12 (M) e terceiro 12 (H). Girei a roleta 5 vezes sem apostar, esperando que um dos conjuntos não aparecesse para que eu pudesse apostar nele, na esperança de que isso aumentasse a probabilidade de sair a meu favor. Após 5 giros, o L não apareceu. Continuei apostando no L, imaginando que os números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 OU 12 sairiam em 12 giros para que eu pudesse pelo menos recuperar meu dinheiro... mas não saíram. A mesa girou 17 vezes seguidas sem um número BAIXO e eu fui de $258 para $0,00... era dinheiro de bônus, de qualquer forma. Esta é uma pergunta em 3 partes:
- O fato de eu ter esperado 5 rodadas sem que um número baixo aparecesse realmente aumentou a probabilidade de sair um L?
- Qual a probabilidade de um número baixo não aparecer 16 vezes seguidas?
- Qual a probabilidade de um número baixo não aparecer 17 vezes seguidas?
Obrigado, também quero agradecer pelo guia de Blackjack. Transformei US$ 5,00 em US$ 100,00 usando seu método.
- Não
- Uma roleta com um único zero é usada no Casino on Net. Portanto, a probabilidade de sair 16 vezes com um zero é (25/37) 16 = 0,1887%.
- (25/37) 17 = 0,1275%.
Qual a probabilidade de um crupiê acertar 5 números iguais em 10 giros da roleta?
A probabilidade de qualquer número ocorrer exatamente 5 vezes em 10 rodadas em um jogo de roleta com duplo zero pode ser aproximada por 38* combin (10,5)*(1/38) 5 *(37/38) 5 = 1 em 359275.
Parabéns pelo excelente site. Entendo perfeitamente sua indignação com a diferença entre os pagamentos de 6 para 5 no Blackjack, mas estou muito curioso para saber por que os americanos parecem aceitar o 00 na Roleta sem questionar. Essa Roleta é quase criminosa e deveria ser classificada no mesmo nível do Keno e das máquinas caça-níqueis.
Obrigado. Você tem razão. A vantagem da casa no blackjack 6 para 5 é de 1,44% pelas regras normais, enquanto na roleta com duplo zero é de 5,26%. Isso é 3,7 vezes pior. No entanto, aprendi ao longo dos anos que é quase impossível fazer com que os jogadores abandonem um jogo de que gostam, independentemente da vantagem da casa. Então, o melhor que posso fazer é aconselhá-los sobre como jogar o jogo de sua preferência. Para os jogadores de blackjack, ainda há muitas opções de jogos 3 para 2 disponíveis. Jogar 6 para 5 dá ao cassino uma vantagem extra de 0,8% sem motivo algum. Também enfatizo a importância de procurar roleta com um único zero se você for um jogador de roleta. Portanto, não vejo nenhuma inconsistência.
Poderia me explicar como funcionam os limites de mesa na roleta e qual a diferença entre o limite mínimo para um número individual e o limite mínimo da mesa? Se possível, por favor, dê exemplos.
Geralmente, existem dois valores mínimos de aposta na roleta. Por exemplo: $5 para apostas externas e $1 para apostas internas. As apostas externas incluem todas as apostas com probabilidades iguais (1/1), apostas em colunas e apostas em dúzias. As apostas internas são aquelas feitas nos números, incluindo grupos de 2, 3, 4, 5 e 6. Nesse caso, o mínimo para apostas externas é de $5 e para apostas internas é de $1. No entanto, você deve apostar pelo menos $5 no total em apostas internas ou não fazer nenhuma aposta.
Eu trabalho em um cassino e tenho uma aposta de que um crupiê de roleta não pode influenciar o resultado de uma jogada. Certamente há quem acredite que isso seja possível. Não em um número específico, é claro, mas talvez em uma parte da roleta. Qual seria um bom teste para determinar, de forma razoável, se um crupiê influenciou os resultados? Supondo que o número de tentativas seja razoável, compartilharei os resultados com prazer.
Estou do seu lado. Se isso fosse possível, os crupiês poderiam facilmente conspirar com os jogadores e dividir os lucros. No entanto, nunca ouvi falar disso acontecer. Um bom teste seria pegar alguém que afirma ser capaz de influenciar o resultado dos lançamentos e pedir que essa pessoa tente acertar um número específico em uma das metades da roleta o máximo de vezes possível ao longo de 100 giros. Quanto mais vezes ela conseguir, maior será o peso da sua afirmação. A tabela abaixo mostra a probabilidade de 50 a 70 giros bem-sucedidos. Por exemplo, a probabilidade de 60 ou mais giros bem-sucedidos é de 2,8444%. Limiares de confiança comuns em estatística são os níveis de 90%, 95% e 99%. Para superar um teste de confiança de 90%, no qual a probabilidade de falha em giros aleatórios é de 90%, o número de giros bem-sucedidos precisaria ser de 57 ou mais. Para superar um teste de 95%, o número precisaria ser de 59 ou mais, e em 99%, o número precisaria ser de 63 ou mais.
Probabilidade de pelo menos 50 a 70 giros bem-sucedidos na roleta.
| Vitórias | Probabilidade |
| 70 | 0,000039 |
| 69 | 0,000092 |
| 68 | 0,000204 |
| 67 | 0,000437 |
| 66 | 0,000895 |
| 65 | 0,001759 |
| 64 | 0,003319 |
| 63 | 0,006016 |
| 62 | 0,010489 |
| 61 | 0,0176 |
| 60 | 0,028444 |
| 59 | 0,044313 |
| 58 | 0,066605 |
| 57 | 0,096674 |
| 56 | 0,135627 |
| 55 | 0,184101 |
| 54 | 0,242059 |
| 53 | 0,30865 |
| 52 | 0,382177 |
| 51 | 0,460205 |
| 50 | 0,539795 |
O site www.ccc-casino.com não possui roleta com zero, que eles chamam de Super Chance Roulette. Existem sistemas que seriam eficazes sem o zero? Sem o zero, seria possível jogar tanto no preto quanto no vermelho simultaneamente, já que não há o risco de perder o zero?
Tentei encontrar esse jogo, mas o site estava fora do ar quando verifiquei. No entanto, supondo que tal jogo existisse, a resposta é não. Nenhum sistema conseguiria vencê-lo, nem perder para ele, a longo prazo. O valor esperado de cada sistema seria exatamente zero.
Roleta com um único zero. Qual a probabilidade de um mesmo número (de 0 a 36) sair mais de uma vez em três rodadas consecutivas? Obrigado pela atenção!
Independentemente do primeiro número, a probabilidade de apenas o segundo giro coincidir com ele é (1/37)*(36/37). A probabilidade de apenas o terceiro giro coincidir com ele é (36/37)*(1/37). A probabilidade de nenhum giro coincidir, mas o segundo e o terceiro coincidirem entre si, é (36/37)*(1/37). A probabilidade de ambos os giros coincidirem com ele é (1/37)*(1/37). Somando tudo isso, obtemos 3*(1/37)*(36/37) + (1/37)*(1/37) = 7,962%.
Acho que você pode se interessar por isso. Eu uso a Betfair aqui no Reino Unido. Tenho certeza de que vocês, americanos, não podem usá-la por algum motivo. De qualquer forma, se você não a conhece, acesse betfair.co.uk e dê uma olhada. É uma bolsa de apostas, não uma casa de apostas tradicional. Enfim, minha pergunta é a seguinte: eles agora oferecem roleta SEM ZERO, isso mesmo, sem zero. É verdade mesmo. Você consegue pensar em uma boa estratégia que eu possa usar? E, se conseguir, guarde-a para você? Atenciosamente, Jonathan. PS: Eles também oferecem outros jogos de cassino sem vantagem da casa.
Tentei criar uma conta lá para testar, mas eles bloqueiam jogadores dos EUA. Me disseram que a aposta mínima é de £2 e a máxima é de £50. Mesmo em um jogo com vantagem da casa zero, como a roleta sem zero, ainda não existe um sistema de apostas que consiga ficar acima ou abaixo desse percentual de 0%. Não importa o que você faça, quanto mais você joga, mais perto de 0% fica o lucro real da casa.
Você diz que não existe um sistema vencedor na roleta. Gonzalo Garcia-Pelayo e sua família ganharam muito dinheiro em diversos cassinos ao redor do mundo. Eles até publicaram um livro, descrevendo como conseguiram. Qual a sua opinião?
Vi um programa de televisão sobre ele uma vez e aplaudo o que ele fez. O que eu defino como um "sistema" é um padrão de apostas, como o Martingale , aplicado a um jogo com vantagem da casa, como uma roleta justa. O que Gonzalo Garcia-Pelayo fez com sucesso foi analisar a frequência com que a bola caía em cada número, numa tentativa de encontrar e explorar roletas viciadas. Isso eu chamaria de estratégia, em oposição a um sistema. Existem muitas estratégias lucrativas para vencer os cassinos, mas nenhum sistema de apostas lucrativo.
Se eu lhe mostrar um jogo de roleta sem zeros e com todas as regras usuais da roleta aplicadas, é possível ganhar 100% das vezes?
Não.
Sou assinante do seu boletim informativo há muito tempo e continuo adorando seu site. Encontrei um site de cassino que oferece roleta sem nenhum zero na roda. Ela só tem os números de 1 a 36, e todas as regras padrão da roleta se aplicam. Você vê alguma maneira de tirar proveito disso? Sei que você não gosta de sistemas de apostas, mas neste caso não há vantagem da casa. Deve haver algum sistema de gerenciamento de banca que possa funcionar de forma lucrativa com esses limites de mesa. Qualquer conselho será bem-vindo.
Obrigado pelas palavras gentis. Acho que já respondi a essa pergunta antes, mas não, mesmo com vantagem da casa zero, ainda não existe um sistema de apostas que possa ser vencedor a longo prazo.
Olá, por razões óbvias, agradeceria se não compartilhasse meu nome com ninguém. No cassino onde trabalho, há praticamente unanimidade entre os crupiês de roleta de que conseguem "controlar o giro" e acertar certas seções da roleta com facilidade ou errar outras de propósito. Considerando todos os fatores que influenciam o giro da bola na roleta, incluindo as ondulações laterais, a direção da bola e a velocidade da roleta, etc., você acha que isso tem algum fundamento? Seria suficiente para um crupiê desonesto ajudar um jogador a superar a enorme vantagem da casa?
Esta não é a primeira vez que ouço essa afirmação, e sou muito cético quanto a ela. A maioria dos crupiês também acredita em mitos como o de que um jogador ruim na terceira base fará com que os outros jogadores percam no blackjack, então, como grupo, eles não são os mais céticos. O que eu acho que acontece é que eles se lembram das vezes em que conseguiram controlar a rodada e convenientemente se esquecem das vezes em que não conseguiram. Assim como se lembram das vezes em que o jogador da terceira base pegou a carta que estourou do crupiê, mas se esquecem das vezes em que ele salvou a mesa.
Se os crupiês realmente pudessem fazer isso, seria fácil ter um cúmplice jogando, fazendo com que ele ganhasse e os outros jogadores perdessem, para compensar. Contanto que seguissem os procedimentos corretos para a rodada e não aparecessem em público com o cúmplice, tudo pareceria completamente legítimo. No entanto, você nunca ouve falar disso acontecendo. Suponho que os que acreditam nisso possam dizer que aqueles que fazem isso estão apenas tentando manter um perfil discreto, mas é isso que os que acreditam em sistemas de apostas inúteis também dizem. Se fosse tão fácil quanto os crupiês da roleta onde você trabalha afirmam, o problema da trapaça seria generalizado.
Na roleta de duplo zero, qual é a probabilidade de que nenhum número tenha sido sorteado até a 200ª rodada?
A probabilidade de um determinado número não ter sido atingido é (37/38) 200 = 0,48%.
Com 38 números, poderíamos dizer incorretamente que a probabilidade de que qualquer um deles não seja atingido é 38 × (37/38) 200 = 18,34%.
O motivo pelo qual isso está incorreto é que conta duas vezes dois números que não foram acertados. Portanto, precisamos subtrair essas probabilidades. Existem combin (38,2) = 703 conjuntos de 2 números em 38. A probabilidade de não acertar quaisquer dois números dados é (36/38) × 200 = 0,000020127. Precisamos subtrair a probabilidade de evitar ambos os números. Assim, temos:
38×(37/38) 200 - combinar(38,2)×(36/38) 200 = 16,9255%.
No entanto, agora anulamos a probabilidade de três números não serem sorteados. Para qualquer grupo de três números, triplicamos a probabilidade de qualquer número individual não ser sorteado. Em seguida, triplicamos a probabilidade de cada forma de escolher dois números dentre os três, resultando em zero para a probabilidade de que nenhum dos três números seja sorteado. Existem combin(38,3) = 8.436 grupos desse tipo. Somando-os novamente, chegamos a:
38×(37/38) 200 - combinar(38,2)×(36/38) 200 + combinar(38,3)×(35/38) 200 = 16,9862%.
No entanto, agora superestimamos a probabilidade de quatro números não aparecerem. Para cada um dos combin(38,4)=73.815 grupos de quatro números, cada um foi originalmente contado quatro vezes. Em seguida, subtraímos cada um dos combin(4,2)=6 grupos de 2 números dentre os 4. Depois, adicionamos novamente os 4 grupos de 3 números dentre os 4. Portanto, para cada união de quatro números, ela foi contada 4 − 6 + 4 = 2 vezes. Para ajustar a contagem dupla, devemos subtrair para cada grupo. Subtraindo-os, chegamos a:
38×(37/38) 200 - combinar(38,2)×(36/38) 200 + combinar(38,3)×(35/38) 200 - combinar(38,4)×(34/38) 200 = 16,9845%.
Continuando o processo, alternaríamos entre somar e subtrair até faltarem 37 números. Portanto, a probabilidade de pelo menos um número nunca ser acertado é:
Soma de i=1 a 37 [(-1) (i+1) × combin(38,i) × ((38-i)/38) 38 ] = 16,9845715651245%
Aqui estão os resultados de uma simulação aleatória de 126.900.000 experimentos desse tipo, com 200 spins.
Números sorteados em 200 giros da roleta
| Números atingidos | Observações | Razão |
|---|---|---|
| 31 ou menos | 0 | 0 |
| 32 | 1 | 0,00000001 |
| 33 | 33 | 0,00000026 |
| 34 | 1812 | 0,00001428 |
| 35 | 68845 | 0,00054251 |
| 36 | 1577029 | 0,01242734 |
| 37 | 19904109 | 0,15684877 |
| 38 | 105348171 | 0,83016683 |
| Total | 126900000 | 1 |
A proporção de vezes em que pelo menos um número não foi atingido foi de 0,169833.
Tenho um amigo que trabalhava em um cassino e era responsável pelas mesas de roleta. Ele me contou que, quando os jogadores começam a ganhar, o cassino troca o crupiê. Também já vi um funcionário pedir a um crupiê para girar a roleta em uma velocidade diferente. Isso não significa que os cassinos têm certeza de que o crupiê pode influenciar a ordem dos números sorteados? Isso não significa que um jogador pode procurar uma mesa "da sorte", onde o crupiê, ao girar a roleta regularmente, aumenta suas chances de ganhar?
Infelizmente, a ignorância pode chegar a níveis muito altos. Não questiono que um especialista consiga prever o resultado em uma roleta girando muito lentamente. No entanto, deixando isso de lado, trocar de crupiê não altera as probabilidades. Não existe crupiê sortudo ou azarado. É difícil se livrar da superstição. Como já disse muitas vezes, quanto mais ridícula uma crença, mais tenazmente ela tende a ser mantida.
Prezado senhor, registrei 8672 jogos de roleta automática com um único zero. Meu número predeterminado saiu incríveis 278 vezes. Escolhi esse número devido ao desgaste da carteira. Quão certo posso estar de que esse número tem uma probabilidade maior que 1/37?
Se minha terminologia estiver correta, "calcular a velocidade da roleta" significa prever onde a bola vai cair, levando em consideração a velocidade, a posição e a rotação da roleta. Parece que você está explorando uma roleta viciada, o que é uma jogada de vantagem diferente. Já que estamos falando sobre isso, uma terceira jogada de vantagem é explorar a "assinatura do dealer", quando o crupiê é tão consistente que a velocidade da bola e da roleta são quase as mesmas a cada giro. Isso permite que o jogador preveja onde a bola vai cair com base na posição da bola e em resultados anteriores.
Para responder à sua pergunta, o número esperado de vezes que você deveria ter acertado o seu número é 8672/37 = 234,38. A variância é 8672 × (1/37) × (36/37) = 228,04. O desvio padrão é a raiz quadrada da variância, ou 15,10. Você teve 278 - 234,38 = 43,62 acertos a mais do que o esperado. Isso corresponde a (43,62 - 0,5)/15,10 = 2,8556 desvios padrão. A razão para subtrair 0,5 é difícil de explicar. Basta dizer que é um fator de ajuste para usar uma função contínua para estimar uma função discreta. Fazendo uma aproximação gaussiana, a probabilidade de acertar o seu número tantas vezes, ou mais, é de 0,21%. Portanto, há uma boa chance de você ter encontrado uma roleta viciada. No entanto, ainda existe uma chance de 1 em 466 de que tenha sido apenas sorte.
Há uma história famosa sobre uma competição de "freeze-out" entre um jogador japonês de apostas altas, Kashiwagi, e Donald Trump, que ocorreu há 20 anos. Kashiwagi não podia apostar mais de US$ 200 mil por mão no bacará. O jogo terminaria quando o cassino ou o jogador estivesse com uma vantagem de US$ 12 milhões. Suponha que Kashiwagi sempre aposte o máximo no Banqueiro. Qual é a probabilidade de Kashiwagi vencer?
Os cálculos ficam mais fáceis se ele apostar no Jogador. Eu resolvo um problema semelhante na roleta no meu site mathproblems.info, problema número 116. Para apostas com probabilidades iguais, a fórmula geral é ((q/p) b -1)/((q/p) g -1), onde:
b = saldo inicial em unidades.
g = meta de saldo bancário em unidades.
p = probabilidade de ganhar qualquer aposta, sem contar empates.
q = probabilidade de perder uma aposta específica, sem contar empates.
Aqui, o jogador começa com 12 milhões de dólares, ou 60 unidades de 200.000 dólares, e jogará até atingir 120 unidades ou perder tudo. Portanto, no caso da aposta do Jogador, os valores da equação são:
b = 60
g = 120
p = 0,493175
q = 0,506825
Portanto, a resposta é ((0,506825/0,493175) 60 -1)/(( 0,506825/0,493175) 120 -1) = 16,27%.
Na aposta no Banqueiro, a situação é bem mais complexa devido à comissão de 5%. Isso resulta na possibilidade real de o jogador ultrapassar sua meta. Se adicionarmos a regra de que, caso uma aposta vencedora permita ao jogador atingir seu objetivo, ele só poderá apostar o necessário para chegar exatamente a US$ 12 milhões, estimo sua probabilidade de sucesso em 21,66%.
Uma fórmula mais simples para a probabilidade de dobrar um saldo bancário é 1/[1+(q/p) b].
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Em média, quantas rodadas seriam necessárias em uma roleta de 38 números antes que algum número se repetisse?
Considerando o primeiro ensaio, mostro que a média é 8,408797, a mediana é 8 e a moda é 7.
A probabilidade de dois números não se repetirem é 37/38 = 97,37%.
A probabilidade de três números sem repetição é (37/38)×(36/38) = 92,24%.
A probabilidade de quatro números sem repetição é (37/38)×(36/38)×(35/38) = 84,96%.
Seguindo esse padrão, a probabilidade de não haver repetições em 8 números é (37/38)×(36/38)×(35/38)×...×(31/38) = 45,35%.
Assim, a probabilidade de uma repetição em um intervalo de 8 números é de 100% - 45,35% = 54,65%.
Imagino que a maioria das pessoas estimaria que a probabilidade de uma repetição em até 8 números seria menor do que isso. Se você não se importa de tirar vantagem dos seus amigos com dificuldades em matemática, proponha uma aposta de que serão necessários 8 números ou menos para que pelo menos um se repita. Assim, você apostaria em 8 ou menos, e seu amigo em 9 ou mais. Se ele/ela hesitar, ofereça-se para apostar em 7 ou mais, o que teria 55,59% de chance de ganhar. Basicamente, quem acertar a mediana de 8 números provavelmente ganhará.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
O programa "Hustling the House" do Discovery Channel teve um longo segmento sobre a melhor maneira de transformar US$ 30 em US$ 1.000. Nele, Andy Bloch dizia: "Se você tem US$ 30 no bolso e quer transformá-los em US$ 1.000, a roleta é o único jogo que você pode jogar." Andy então explicou por que apostar os US$ 30 inteiros em um único número era melhor do que fazer cinco apostas com probabilidades iguais.
Andy está certo ao afirmar que a melhor maneira de transformar US$ 30 em US$ 1.000 é apostar os US$ 30 em um único número na roleta?
Não, ele não está correto. A probabilidade da estratégia de aposta única de Andy é 1/38 = 2,6316%.
Após muitas tentativas e erros, desenvolvi minha estratégia de roleta "Ave Maria", que aumentará as chances de transformar US$ 30 em US$ 1.000 para 2,8074%.
A estratégia "Ave Maria" do mago para a roleta:
Essa estratégia pressupõe que as apostas devem ser feitas em incrementos de US$ 1. Em todos os cálculos de apostas, arredonde para baixo.
Deixar:
b = Seu saldo bancário
g = Seu objetivo
- Se 2*b >=g, então aposte (gb) em qualquer aposta de probabilidade igual.
- Caso contrário, se 3*b >=g, então aposte (gb)/2 em qualquer coluna.
- Caso contrário, se 6*b >=g, então aposte (gb)/5 em qualquer linha de seis (seis números).
- Caso contrário, se 9*b >=g, então aposte (gb)/8 em qualquer canto (quatro números).
- Caso contrário, se 12*b >=g, então aposte (gb)/11 em qualquer rua (três números).
- Caso contrário, se 18*b >=g, então aposte (gb)/17 em qualquer divisão (dois números).
- Caso contrário, aposte (gb)/35 em qualquer número único.
Em outras palavras, tente sempre atingir o objetivo com apenas uma aposta, se possível, sem ultrapassá-lo. Se houver várias maneiras de alcançar esse objetivo, escolha aquela com a maior probabilidade de vitória.
E quanto a outros jogos, você pode perguntar? Segundo o narrador do Discovery Channel, "Todo mundo concorda que a roleta é o melhor esquema para ficar rico rápido no cassino". Bem, eu não concordo. Mesmo nos limitando a jogos e regras comuns, acho o craps melhor. Em particular, apostar no "don't pass" e fazer apostas com odds altas.
Seguindo minha estratégia de "Aposta Alta" para craps (explicada abaixo), a probabilidade de transformar US$ 30 em US$ 1.000 é de 2,9244%. Isso pressupõe que o jogador possa apostar com odds de 6x, independentemente do ponto (o que ocorre quando odds de 3x, 4x e 5x são permitidas). Essa probabilidade de sucesso é 0,117% maior do que a minha estratégia de "Aposta Alta" para roleta e 0,2928% maior do que a estratégia de Andy Bloch.
Andy poderia argumentar que meu argumento acima se baseia na premissa de uma aposta mínima de US$ 1, o que é difícil de encontrar em Las Vegas em jogos com crupiê ao vivo. Prevendo que alguém pudesse dizer isso, simulei ambos os jogos considerando uma aposta mínima de US$ 5 e apostando em incrementos de US$ 5. Nesse caso, a probabilidade de sucesso usando minha estratégia "Hail Mary" é de 2,753% na roleta e de 2,891% no craps. Em ambos os casos, maior que os 2,632% da estratégia de Andy Bloch.
Para ser justo, o Discovery Channel jamais teria exibido aquele discurso insano acima e certamente buscava algo simples que o público em geral pudesse entender. Andy, sem dúvida, estava oferecendo algo que eles queriam ouvir. A premissa básica de seu conselho é que, se você quer atingir um determinado objetivo, uma estratégia de "aposta rápida e fuga" é muito melhor do que deixar a vantagem da casa te desgastar com múltiplas apostas. Isso é definitivamente verdade e algo que venho defendendo há 17 anos.
A estratégia "Ave Maria" do mago para o jogo de dados.
Essa estratégia pressupõe que as apostas devem ser feitas em incrementos de US$ 1 e os ganhos serão arredondados para baixo, para o dólar mais próximo. Ao calcular as apostas, nunca aposte um valor que ultrapasse a meta. Além disso, nunca faça uma aposta que resulte em arredondamento para baixo.
Deixar:
b = Seu saldo bancário
g = Seu objetivo
- Aposte max($1,min(b/7,(gb)/6)) no não passe.
- Se um ponto for sorteado e você tiver o suficiente para uma aposta com odds completas, então aposte contra as odds completas. Caso contrário, aposte contra o que você puder.
Então, espero que Andy e o Discovery Channel estejam felizes. Passei dias fazendo simulações para provar que eles estavam errados.
Essa questão foi levantada e discutida no meu fórum, Wizard of Vegas .
Qual a probabilidade de a bola cair nos números 1, 2 e 3 em 4, 5, 6, 7, 8 ou 9 giros na roleta?
A fórmula geral é:
Pr(A bola cai na casa 1) + Pr(A bola cai na casa 2) + Pr(A bola cai na casa 3) - Pr(A bola cai nas casas 1 e 2) - Pr(A bola cai nas casas 1 e 3) - Pr(A bola cai nas casas 2 e 3) + Pr(A bola cai nas casas 1, 2 e 3).
Na roleta de duplo zero, para n rodadas, isso resulta em 3*(1-(37/38)^n)-3*(1-(36/38)^n)+(1-(35/38)^n).
A tabela a seguir mostra a probabilidade de se obter os três números para diferentes quantidades de giros, de 3 a 100, na roleta com um ou dois zeros.
Pergunta da roleta
| Giros | Solteiro Zero | Dobro Zero |
|---|---|---|
| 3 | 0,000118 | 0,000109 |
| 4 | 0,000455 | 0,000420 |
| 5 | 0,001091 | 0,001009 |
| 6 | 0,002094 | 0,001939 |
| 7 | 0,003518 | 0,003261 |
| 8 | 0,005404 | 0,005016 |
| 9 | 0,007785 | 0,007234 |
| 10 | 0,010684 | 0,009937 |
| 15 | 0,033231 | 0,031066 |
| 20 | 0,068639 | 0,064476 |
| 25 | 0,114718 | 0,108254 |
| 30 | 0,168563 | 0,159750 |
| 35 | 0,227272 | 0,216265 |
| 40 | 0,288292 | 0,275379 |
| 45 | 0,349548 | 0,335089 |
| 50 | 0,409453 | 0,393835 |
| 55 | 0,466865 | 0,450467 |
| 60 | 0,521017 | 0,504191 |
| 65 | 0,571445 | 0,554501 |
| 70 | 0,617922 | 0,601122 |
| 75 | 0,660393 | 0,643951 |
| 80 | 0,698930 | 0,683016 |
| 85 | 0,733693 | 0,718435 |
| 90 | 0,764897 | 0,750386 |
| 95 | 0,792791 | 0,779086 |
| 100 | 0,817638 | 0,804773 |
Em alguns cassinos do México, eles usam dados em vez de uma roda na roleta. Aqui estão as regras:
- Há quatro dados: dois verdes, um vermelho e um azul.
- Se os dois dados verdes caírem ambos no número um, o resultado da "giro" será zero.
- Se os dois dados verdes caírem ambos no número seis, o resultado da "giro" será um duplo zero.
- Se ocorrer qualquer outro resultado com o dado verde, os 36 resultados possíveis dos dados vermelho e azul serão mapeados para os números 1 e 36 para representar a "rotação".
Como isso altera as probabilidades em comparação com a roleta convencional?
A probabilidade de ganhar com 0 e 00 seria de 1/36 para cada. Se as apostas nesses resultados pagassem o valor usual de 35 para 1, então a vantagem da casa seria exatamente 0%.
A probabilidade de qualquer outro número ser vencedor seria (34/36)*(1/36) = 2,62%. Compare isso com 1/38 = 2,63% na roleta tradicional com duplo zero. A vantagem da casa em qualquer aposta nos números de 1 a 36 seria de 5,56%. Compare isso com os 5,26% na roleta tradicional com duplo zero. Meu conselho neste jogo seria apostar apenas no zero e no duplo zero.
Se alguém puder confirmar ou negar essas regras e pagamentos, por favor, me avise.
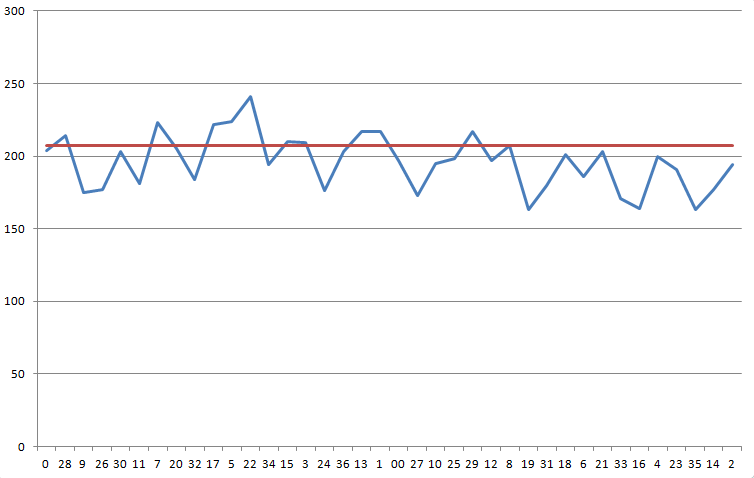
Registrei 7.456 giros na roleta. Os resultados são os seguintes. Suspeito que a roleta esteja viciada, mas não tenho certeza se os dados são conclusivos o suficiente para jogar.
Dados da Roleta
| Vencendo Número | ocorrências |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| Total | 7456 |
O gráfico a seguir mostra seus resultados em ordem sequencial na roleta. A linha azul mostra seus resultados. A linha vermelha representa o número que você precisa, 207,11, para superar a vantagem da casa de 5,26%.
Um teste qui-quadrado nessa distribuição retorna uma estatística de 68,1 com 37 graus de liberdade. A probabilidade de um resultado tão assimétrico ou mais é de 1 em 725.
Não creio que o teste qui-quadrado seja o ideal para esta situação, pois não considera a ordem dos resultados, mas desconheço um teste melhor. Alguns sugeriram o teste de Kolmogorov-Smirnov , mas não o considero apropriado. Se houver outros testes adequados, estou aberto a sugestões.
Posso afirmar que, se você tivesse apostado no arco de 3 números em torno do número 5, teria obtido um lucro de 10,57% nas rodadas registradas. No entanto, se aumentasse para um arco de 7 números, a vantagem cairia para 2,84%.
Se eu tivesse que dar uma resposta em linguagem simples e direta, diria que a roleta apresenta indícios, mas não provas irrefutáveis, de que é viciada. No entanto, esse viés provavelmente não é suficiente para superar de forma significativa e confiável a vantagem da casa. Supondo que o cassino não troque as roletas entre as mesas, eu diria que mais dados deveriam ser coletados antes de apostar grandes quantias de dinheiro. Lamento que esta resposta seja tão vaga.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Na roleta de zero único, qual é o número médio e mediano de giros necessários para que cada número apareça pelo menos uma vez?
Calcular a média é muito mais fácil, então vamos começar por aí. Vamos analisar passo a passo:
- A primeira rodada com certeza vai ser um número novo.
- O segundo giro terá uma probabilidade de 36/37 de resultar em um novo número. Se um evento tem uma probabilidade de p, então o número esperado de tentativas para que ele ocorra é 1/p. Nesse caso, o número esperado de tentativas para obter o segundo número é 37/36 = 1,0278.
- Após dois números terem sido observados, a probabilidade de que a próxima rodada resulte em um novo número é de 35/37. Assim, o número esperado de rodadas após o segundo número para ver o terceiro é de 37/35 = 1,0571.
- Seguindo essa lógica, o número médio de giros para ver cada número é 1 + 37/36 + 37/35 + 37/34 + ... + 37/2 + 37/1 = 155,458690.
A mediana é muito mais complexa. Para encontrar a resposta exata, em vez de usar uma simulação aleatória, é necessário usar muita álgebra matricial. Já discuti como resolver problemas semelhantes em outras perguntas do "Pergunte ao Mago", então não vou repetir os detalhes. Um exemplo de uma questão similar é a de obter um par 6-6 na casa três vezes seguidas, como discutido em "Pergunte ao Mago" nº 311. Basta dizer que a probabilidade de ver todos os números em 145 giros é 0,49161779 e em 146 giros é 0,501522154. Portanto, a mediana é 146.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Se uma bola caiu no vermelho nas últimas 20 rodadas da roleta, qual é a probabilidade de ela cair no preto na próxima rodada?
O mesmo que vermelho, 47,37% em uma roda de duplo zero, 18 números pretos divididos por 38 números no total.
Acho que você está enganado sobre a pergunta anterior. A probabilidade de sair 21 vermelhos seguidos é (18/38) 21 = 1 em 6.527.290. As probabilidades devem favorecer esmagadoramente o preto.
É verdade, mas não importa. A probabilidade é a mesma de sair 20 vermelhos seguidos de um preto. O fato é que o passado não importa em jogos de tentativas independentes como a roleta.
Já pensei em um jeito de vencer os cassinos na roleta! Comece com uma pequena aposta em qualquer resultado com probabilidade de 1 para 1, como vermelho ou preto. Se perder, dobre a aposta na mesma opção. Continue dobrando até ganhar. O resultado vencedor tem que acontecer eventualmente e, quando acontecer, recuperarei minha aposta inicial. Depois, repita o processo. O que você acha? E, por favor, não conte para ninguém.
Este é provavelmente o sistema de apostas mais popular de todos, conhecido como Martingale. Os apostadores o concebem e o utilizam desde tempos imemoriais. Como todos os sistemas de apostas, ele não só não elimina a vantagem da casa, como sequer a reduz. O motivo é que o apostador eventualmente entrará numa sequência de derrotas em que seu saldo não será suficiente para dobrar novamente o valor apostado.
Na sua resposta anterior, você explicou por que a estratégia Martingale não funciona. Então, que tal o oposto, dobrar a aposta após cada vitória até atingir a meta desejada?
Isso é conhecido como anti-Martingale e é igualmente inútil. As vezes em que seu saldo for reduzido a zero superarão os ganhos quando você atingir sua meta. Independentemente do sistema de apostas que você usar, ou nenhum, quanto mais você jogar, mais sua proporção de dinheiro perdido em relação ao dinheiro apostado se aproximará de 5,26% na roleta com duplo zero.
Qual é o número esperado de giros na roleta para se obter cinco vermelhos ou cinco pretos em sequência?
Aqui está minha solução (PDF).
O que é a "lei dos terços" na roleta?
A "lei dos terços" diz que se você girar uma roleta uma vez para cada número nela, cerca de 1/3 dos números nunca sairão.
1/3 é uma estimativa bem ruim. Uma estimativa muito melhor seria 1/e ≈ 36,79%. A porcentagem real, na roleta com duplo zero, é de 36,30%.
A tabela a seguir mostra a probabilidade de se observarem de 1 a 38 números distintos em 38 giros da roleta com duplo zero.
Lei dos Terços -- Roleta com Duplo Zero
| Distinto Números | Probabilidade |
|---|---|
| 1 | 0,000000000 |
| 2 | 0,000000000 |
| 3 | 0,000000000 |
| 4 | 0,000000000 |
| 5 | 0,000000000 |
| 6 | 0,000000000 |
| 7 | 0,000000000 |
| 8 | 0,000000000 |
| 9 | 0,000000000 |
| 10 | 0,000000000 |
| 11 | 0,000000000 |
| 12 | 0,000000000 |
| 13 | 0,000000005 |
| 14 | 0,000000124 |
| 15 | 0,000001991 |
| 16 | 0,000022848 |
| 17 | 0,000191281 |
| 18 | 0,001186530 |
| 19 | 0,005519547 |
| 20 | 0,019434593 |
| 21 | 0,052152293 |
| 22 | 0,107159339 |
| 23 | 0,169042497 |
| 24 | 0,204864337 |
| 25 | 0,190490321 |
| 26 | 0,135436876 |
| 27 | 0,073211471 |
| 28 | 0,029838199 |
| 29 | 0,009063960 |
| 30 | 0,002020713 |
| 31 | 0,000323888 |
| 32 | 0,000036309 |
| 33 | 0,000002742 |
| 34 | 0,000000132 |
| 35 | 0,000000004 |
| 36 | 0,000000000 |
| 37 | 0,000000000 |
| 38 | 0,000000000 |
| Total | 1,000000000 |
A tabela mostra que o resultado mais provável é de 24 números distintos, representando 20,49%. A média é 24,20656478.
Alguns charlatões argumentam que o jogador deve observar os nove primeiros resultados distintos e então apostar neles, acreditando erroneamente que são mais prováveis de ocorrer do que outros números. Isso é totalmente falso! A roleta e a bola não têm memória. Em uma roleta justa, todos os números têm a mesma probabilidade de ocorrer e o passado não importa.