Pergunte ao Mago #227

Há três anos, em uma coluna "Pergunte ao Mago" , você escreveu: "Você está certo ao dizer que 500 lançamentos são poucos para se ter uma boa ideia a favor ou contra a influência nos dados, mas 500 lançamentos são melhores que zero." Você poderia descrever o que exigiria de um suposto influenciador de dados, em um experimento, para que você se sentisse confiante o suficiente para começar a apostar quantias significativas de dinheiro nele? Pergunto isso porque um bilhão de rodadas é um bom parâmetro para resultados "confiáveis" em alguns simuladores de blackjack. Com o design experimental mais eficiente (ou seja, que exige o menor número de lançamentos) que você consegue imaginar, quantos lançamentos o lançador precisaria fazer para ter certeza de que está influenciando os resultados? Sei que a resposta dependerá da habilidade do lançador, mas você entendeu a ideia. Se forem necessários um milhão de lançamentos, mesmo no melhor cenário, não valerá a pena.

Myooligan de Greenfelt

Não existe um ponto definitivo em que se conquista a confiança. É uma questão de grau. Primeiro, eu perguntaria o que está sendo testado e o que o atirador estima que acontecerá. Em qualquer teste, existem dois erros possíveis. Um atirador habilidoso pode falhar por azar, ou um atirador aleatório pode passar por sorte. Entre os dois, eu preferiria evitar um falso positivo. Acho que um teste razoável definiria a probabilidade de um falso negativo em cerca de 5% e a de um falso positivo em cerca de 1%.

Por exemplo, suponha que o requerente diga que consegue, em média, um total de sete a cada sete lançamentos de dados. Um lançador aleatório obteria um sete a cada seis lançamentos, em média. Por tentativa e erro, descobri que um teste que atendesse a ambos os critérios seria lançar os dados 3.600 vezes e exigir 547 ou menos setes para aprovação, ou um sete a cada 6,58 lançamentos.

Um atirador com uma probabilidade de 1 em 7 deveria acertar em média 514,3 setes, com um desvio padrão de 21,00. Usando a aproximação gaussiana, a probabilidade de um atirador habilidoso acertar 548 ou mais setes (um falso negativo) é de 5,7%. Um atirador aleatório deveria acertar em média 600 setes, com um desvio padrão de 22,36. A probabilidade de um atirador aleatório passar no teste (um falso positivo) é de 0,94%. O gráfico abaixo mostra os possíveis resultados para atiradores habilidosos e aleatórios. Se os resultados estiverem à esquerda da linha verde, eu consideraria que o atirador passou no teste e apostaria nele.

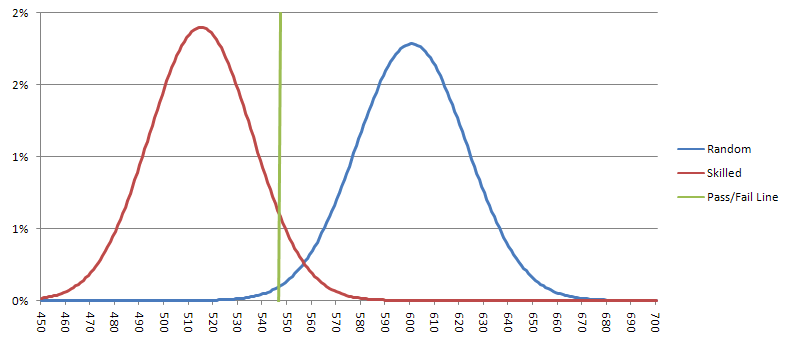
O dilema prático é que, se assumirmos dois lançamentos por minuto, levaria 30 horas para realizar o teste. Talvez eu pudesse ser mais flexível quanto ao nível de significância, para reduzir o tempo necessário, mas os resultados não seriam tão convincentes. Acho que chegou a hora de um teste maior do que o experimento de Wong com 500 lançamentos.

Se a aposta paralela Lucky Lady for jogada apenas quando a contagem verdadeira for, digamos, 10 ou mais, será possível vencer a vantagem da casa? Em caso afirmativo, qual é a contagem verdadeira mínima na qual se pode vencer a vantagem da casa com essa aposta paralela?

Julie Jacques de Morristown, TN

Eu não estudei o efeito da contagem de cartas nessa aposta por mim mesmo. No entanto, Arnold Snyder estudou, e seus resultados podem ser encontrados em seu livro "The Big Book of Blackjack" . Lá, ele diz que você deve fazer a aposta em um jogo com seis baralhos se forem os dois últimos baralhos e a contagem for +10 ou maior, usando a contagem Red Sevens. Em um jogo com dois baralhos, ele diz para apostar no último baralho e com uma contagem de +6 ou maior.

Que vantagem tem um jogador quando a casa permite a desistência tardia em um jogo com 6 baralhos, quando a casa pede carta com 17 suave e quando a casa para no 17 suave? E em um jogo com 8 baralhos?

Sam de Las Vegas

As respostas para perguntas como essa podem ser encontradas usando minha calculadora de vantagem da casa , alterando uma regra e observando o efeito na vantagem da casa. Normalmente eu pediria para você fazer isso, mas estou com paciência hoje, então aqui está:

6 baralhos, dealer para no 17 suave: 0,0726%
8 baralhos, dealer para no 17 suave: 0,0758%
6 baralhos, dealer pede carta no 17 suave: 0,0882%
8 baralhos, dealer pede carta no 17 suave: 0,0916%

Gostaria de saber se existe alguma forma de calcular, em média, quantas tentativas seriam necessárias para perder dez unidades a partir de um ponto qualquer, apostando no Jogador no bacará.

J.J. de Oceanside, CA

A vantagem da casa na aposta do Jogador é de 1,2351%, considerando oito baralhos. O número esperado de mãos necessárias para se ter uma perda de dez unidades é 10/0,012351 = 809,66.

Recentemente, estava jogando pôquer em casa (Omaha Deuces Wild) com alguns familiares. Havia cinco jogadores, e restaram apenas dois. Eu era um deles. A outra jogadora vinha ganhando a noite toda. Finalmente, consegui uma boa mão. Olhei para ela e, em tom de deboche, gritei "quatro setes". Ela disse que tinha quatro ases e começou a recolher as fichas. Corrigi-me e disse que tinha um straight flush. Ela então me disse que eu já havia pago com o quatro setes. Mostrei minha mão e ela continuou insistindo que eu já havia pago com o quatro setes e que minha mão não era mais boa. Então, a questão é: quem ganhou a mão? Claramente, o straight flush vence uma quadra. Mas será que eu descartei minha mão ao dizer o que disse? O dinheiro ainda estava na mesa.

Don de Lihue, HI

No fim das contas, as cartas falam por si. Você deveria ter ganhado aquela mão.