Pergunte ao Mago #230

Q: Prezado senhor, registrei 8672 jogos de roleta automática com um único zero. Meu número predeterminado saiu incríveis 278 vezes. Escolhi esse número devido ao desgaste da carteira. Quão certo posso estar de que esse número tem uma probabilidade maior que 1/37?

Se minha terminologia estiver correta, &quot;calcular a velocidade da roleta&quot; significa prever onde a bola vai cair, levando em consideração a velocidade, a posição e a rotação da roleta. Parece que você está explorando uma roleta viciada, o que é uma jogada de vantagem diferente. Já que estamos falando sobre isso, uma terceira jogada de vantagem é explorar a &quot;assinatura do dealer&quot;, quando o crupiê é tão consistente que a velocidade da bola e da roleta são quase as mesmas a cada giro. Isso permite que o jogador preveja onde a bola vai cair com base na posição da bola e em resultados anteriores.<p> Para responder à sua pergunta, o número esperado de vezes que você deveria ter acertado o seu número é 8672/37 = 234,38. A variância é 8672 × (1/37) × (36/37) = 228,04. O desvio padrão é a raiz quadrada da variância, ou 15,10. Você teve 278 - 234,38 = 43,62 acertos a mais do que o esperado. Isso corresponde a (43,62 - 0,5)/15,10 = 2,8556 desvios padrão. A razão para subtrair 0,5 é difícil de explicar. Basta dizer que é um fator de ajuste para usar uma função contínua para estimar uma função discreta. Fazendo uma aproximação gaussiana, a probabilidade de acertar o seu número tantas vezes, ou mais, é de 0,21%. Portanto, há uma boa chance de você ter encontrado uma roleta viciada. No entanto, ainda existe uma chance de 1 em 466 de que tenha sido apenas sorte.

Hoje, as notícias contam que uma mulher em Atlantic City rolou 154 dados consecutivos antes de tirar um sete no Borgata . Isso significa que ela rolou dois dados 154 vezes, sem nenhum sete. Então, calculei (30/36) ¹⁵⁴ e cheguei a uma probabilidade de mais de 1,5 trilhão para 1. É cerca de 9.000 vezes mais provável ganhar na loteria Mega Millions do que conseguir uma maratona de 154 lançamentos consecutivos de dados sem tirar o sete. Considerando o quão astronomicamente improvável isso é, e considerando que pessoas são condenadas com base em evidências de DNA com probabilidades de bilhões para um de serem falsas, o quanto você suspeitaria de fraude e se ofereceria para consultar o Borgata sobre isso? Eu já liguei para eles, dei meu nome e disse para fazerem o que quiserem com a informação. Gostaria de saber sua opinião.

Adam

Primeiramente, ela lançou os dados um total de 154 vezes, sendo que o 154º lançamento resultou em um sete ( Fonte: NJ.com ). No entanto, isso não significa que ela nunca tenha tirado um sete nos primeiros 153 lançamentos. Ela poderia ter tirado muitos deles nos lançamentos iniciais. Como mostrei em minha coluna de 3 de maio de 2003 , a probabilidade de chegar ao 154º lançamento é de 1 em 5,6 bilhões. As chances de ganhar na Mega Millions são de 1 em combin (56,5)*46 = 175.711.536. Portanto, chegar a 154 lançamentos ou mais é cerca de 32 vezes mais difícil. Dado tempo suficiente e tabelas, que acredito existirem, algo assim acabaria acontecendo mais cedo ou mais tarde. Então, eu não suspeitaria de trapaça. Estimo que a probabilidade de isso acontecer em qualquer ano seja de aproximadamente 1%.

Veja também minha solução, expressa em matrizes, em mathproblems.info , problema 204.

Os cassinos Station oferecem cartelas de bingo "Mini X" gratuitas aos seus jogadores, de acordo com o valor gasto, conforme segue:

Gaste de US$ 1 a US$ 19 e ganhe 1 cartão grátis.
Gaste de US$ 20 a US$ 29 e ganhe 2 cartões grátis.
Gaste de US$ 30 a US$ 39 e ganhe 3 cartões grátis.
Gaste de US$ 40 a US$ 49 e ganhe 4 cartões grátis.
Gaste entre US$ 50 e US$ 59 e ganhe 5 cartões grátis.
Gaste US$ 60 ou mais e ganhe 6 cartões grátis.

Cada cartela contém cinco números, um para cada letra da palavra BINGO. Os prêmios são os seguintes:

Cartão de cobertura com 5 números = $10.000
Cartão de capa com 6 números = $3.000
Cartão de capa com 7 números = $500

Caso ninguém consiga cobrir os números em 7 ou menos, um prêmio de consolação de $50 será pago ao primeiro jogador que o fizer.

Minha pergunta é: qual o valor esperado de cada carta?

Edward de Forks, WA

A tabela a seguir mostra que o valor dos prêmios básicos é de 1/5 de um centavo por cartão.

Valor esperado do cartão Mini X

Chamadas	Paga	Probabilidade	Retornar
5	10000	0,00000006	0,00057939
6	3000	0,00000029	0,00086909
7	500	0,00000087	0,00043455
Total		0,00000122	0,00188303

O valor do prêmio de consolação por cartão é de 50/n, onde n é o número de cartões concorrentes. Por exemplo, se houvesse 1000 cartões concorrentes, o valor do prêmio de consolação por cartão seria de 5 centavos.

Na sua página de estratégia para video poker double double bonus poker , você afirma que se receber 5 cartas,

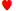Que é correto segurar a sequência. Parece-me contraintuitivo, mas se você pudesse explicar com um pouco mais de detalhes por que tentar o straight flush é uma estratégia ruim, eu agradeceria.

David de Montego Bay

No Double Double Bonus, um Straight Flush paga 50, um Flush paga 6 e uma Sequência paga 4. A probabilidade de formar um Straight Flush é 2/47, de um Flush é 7/47 e de uma Sequência é 5/47. Portanto, o retorno esperado ao descartar o 9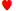

é (2/47)×50 + (7/47)×6 + (5/47)×4 = 3,4468. O retorno esperado da reta em 4 é muito maior.

O que aconteceu com o jogo de cartas 3-5-7 em Las Vegas? Não consigo encontrá-lo em lugar nenhum.

Vince de North Collins, NY

Fui informado de que esse jogo teve que ser retirado dos cassinos dos EUA por infringir a patente. De acordo com o Relatório Estatístico do Quarto Trimestre de 2008 do Conselho de Controle de Jogos de Nevada, os números de jogos de mesa no Condado de Clark são os seguintes.

Contagem de jogos de mesa do Condado de Clark

Jogo	Tabelas
21	2537
Roleta	405
Dados	334
Outro	243
Bacará	233
Pôquer de três cartas	208
Pôquer Pai Gow	194
Mini bacará	143
Deixe-o andar	98
Pai Gow	80
Roda da Fortuna (Seis Grandes)	37
Caribbean Stud Poker	22
Sic Bo	1
Chuck-a-Luck	1

Infelizmente, eles não dizem quais são os outros 243 jogos "extras", então isso não ajuda muito a responder sua pergunta, mas ainda assim vale a pena mencionar.

Prezado senhor, registrei 8672 jogos de roleta automática com um único zero. Meu número predeterminado saiu incríveis 278 vezes. Escolhi esse número devido ao desgaste da carteira. Quão certo posso estar de que esse número tem uma probabilidade maior que 1/37?

Marc de Rotterdam, Netherlands

Se minha terminologia estiver correta, "calcular a velocidade da roleta" significa prever onde a bola vai cair, levando em consideração a velocidade, a posição e a rotação da roleta. Parece que você está explorando uma roleta viciada, o que é uma jogada de vantagem diferente. Já que estamos falando sobre isso, uma terceira jogada de vantagem é explorar a "assinatura do dealer", quando o crupiê é tão consistente que a velocidade da bola e da roleta são quase as mesmas a cada giro. Isso permite que o jogador preveja onde a bola vai cair com base na posição da bola e em resultados anteriores.

Para responder à sua pergunta, o número esperado de vezes que você deveria ter acertado o seu número é 8672/37 = 234,38. A variância é 8672 × (1/37) × (36/37) = 228,04. O desvio padrão é a raiz quadrada da variância, ou 15,10. Você teve 278 - 234,38 = 43,62 acertos a mais do que o esperado. Isso corresponde a (43,62 - 0,5)/15,10 = 2,8556 desvios padrão. A razão para subtrair 0,5 é difícil de explicar. Basta dizer que é um fator de ajuste para usar uma função contínua para estimar uma função discreta. Fazendo uma aproximação gaussiana, a probabilidade de acertar o seu número tantas vezes, ou mais, é de 0,21%. Portanto, há uma boa chance de você ter encontrado uma roleta viciada. No entanto, ainda existe uma chance de 1 em 466 de que tenha sido apenas sorte.