Pergunte ao Mago #259
Em alguns cassinos na Holanda, é permitido o triplo aprisionamento na roleta. Qual é a vantagem da casa para apostas com probabilidades iguais sob essa regra? Estou mais interessado na solução do que na resposta.
Para benefício de outros leitores, em muitos cassinos na Europa, se você fizer uma aposta de probabilidade igual na roleta e a bola cair no zero, a aposta fica "presa". Se a próxima jogada resultar em uma vitória, a aposta é devolvida sem ganhos. Se a bola cair no lado oposto, a aposta é perdida.
O que acontece com apostas de prisão simples se a bola cair no zero? Se o cassino permitir apenas prisão simples, a aposta será perdida. No entanto, alguns cassinos permitem prisão dupla, que é o que aconteceria. Se uma aposta com prisão dupla for vencedora, ela volta a ser de prisão simples. Se o cassino permitir apenas até prisão dupla, uma aposta com prisão dupla perderia se caísse outro zero. Pela mesma lógica, se um cassino permitir prisão tripla, uma aposta com prisão dupla se tornaria prisão tripla se caísse outro zero.
A vantagem da casa no aprisionamento triplo é de 1,370120%. Antes de explicar como cheguei a esse resultado, vamos analisar primeiro o aprisionamento simples e o duplo. Suponha que a primeira aposta seja no vermelho.
Seja Z = probabilidade de zero = 1/37.
Seja R = probabilidade de um número vermelho = 18/37.
prisão individual
pr(push) = ZR = 0,0131482834.
pr(win) = R = 0,4864864865.
pr(perda) = 1-pr(push)-pr(vitória) = 0,5003652301.
Valor esperado = pr(vitória)-pr(derrota) = -0,0138787436.
Dupla prisão
O jogador empurra se a primeira rodada for zero, podendo então repetir ZR de 0 até um número infinito de vezes, até obter um vermelho. Em outras palavras, as maneiras de empurrar são:
ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...
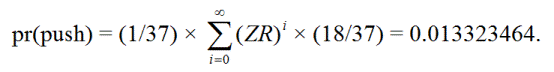
pr(push) = 0,013323464
pr(win) = 18/37 = 0,4864864865.
pr(perda) = 1-pr(push)-pr(vitória) = 0,5001900494.
Valor esperado = pr(vitória)-pr(derrota) = -0,0137035629.
Tripla prisão
Primeiro, vamos encontrar a probabilidade p 1 de que uma aposta inicialmente "aprisionada" se torne triplamente "aprisionada" com mais dois zeros e, eventualmente, volte a ser uma aposta individual aprisionada. Isso pode acontecer da seguinte forma:
ZZRR, ZZ(RZ)RR, ZZ(RZ)(RZ)RR, ZZ(RZ)(RZ)(RZ)RR, ...
Em outras palavras, a aposta pode oscilar entre prisão tripla e dupla um número infinito de vezes.
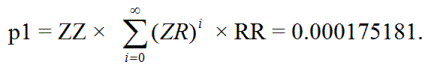
Em segundo lugar, seja p 2 = a probabilidade de uma aposta com prisão simples atingir o primeiro ou segundo nível de prisão e depois retornar à prisão simples.
seja p 2 = ZR + p 1 = 0,013323464.
O jogador pode repetir o processo de retornar ao primeiro nível, partindo de zero, um número infinito de vezes. Portanto, a probabilidade de um empurrão é:
ZR + Z p 2 R + Z p 2 p 2 R + Z p 2 p 2 p 2 R + ... =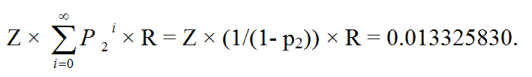
Z × (1/(1- p 2 )) × R = 0,013325830.
pr(push) = 0,013325830.
pr(win) = 18/37 = 0,4864864865.
pr(perda) = 1-pr(push)-pr(vitória) = 0,5001876839.
Valor esperado = pr(vitória)-pr(derrota) = -0,0137011974.
Prisão infinita
Não que você tenha perguntado, Maff, mas ouvi dizer que na Espanha permitem prisão perpétua. Seja p a probabilidade de um empurrão. Essa também é a probabilidade de começar no nível x de prisão, cair em níveis cada vez mais baixos, mas eventualmente voltar a subir para x.
p = ZR + ZpR + ZppR + ZpppR + ...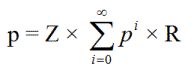
p 2 - p + ZR = 0
Pela fórmula quadrática p = (1-(1-4*RZ) 1/2 )/2 = 0,0133258620.
pr(push) = 0,0133258620.
pr(win) = 18/37 = 0,4864864865.
pr(perda) = 1-pr(push)-pr(vitória) = 0,5001876515.
Valor esperado = pr(vitória)-pr(derrota) = -0,0137011650.
Zeros ignoraram a prisão
Finalmente, em alguns cassinos, os zeros são simplesmente ignorados após o primeiro zero que prende a aposta. Nesses casos, a probabilidade de um empate é simplesmente (1/37)×(1/2) = 0,0135135135.
A tabela a seguir resume os quatro tipos de regras.
Probabilidades de prisão
| Prisão | Ganhar | Empurrar | Perda | Esperado Valor |
| Solteiro | 0,48648649 | 0,01314828 | 0,50036523 | -0,01387874 |
| Dobro | 0,48648649 | 0,01332346 | 0,50019005 | -0,01370356 |
| Triplo | 0,48648649 | 0,01332583 | 0,50018768 | -0,01370120 |
| Infinito | 0,48648649 | 0,01332586 | 0,50018765 | -0,01370117 |
| Zeros ignorados | 0,48648649 | 0.01351351 | 0,50000000 | -0,01351351 |
Gostaria de agradecer a ChesterDog e weaselman pela ajuda matemática. Gostaria também de agradecer e mencionar o professor G. Artico e o site polarprof.it pelo código HTML da fórmula de somatório acima.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Considere que o seguinte se aplica a uma única máquina de videopôquer.
- Bônus progressivo 6-5 no Poker.
- Aumento de 2% no medidor no royal flush.
- Jogo de 5 moedas.
Agora, imagine o seguinte a meu respeito.
- Retorno mínimo ao jogo de 100,5%.
- Sou capaz de jogar uma sequência progressiva até acertar.
- Conheço a estratégia perfeita de Bonus Poker 6-5 para um Royal Flush de 4000 moedas.
Qual o valor mínimo do prêmio para eu poder jogar?
7.281,8 moedas. É interessante notar que, se você jogasse apenas uma vez exatamente nesse ponto, o retorno seria de apenas 98,5%. O motivo para jogar nesse ponto é a suposição de que você é capaz de jogar até ganhar o jackpot. É como ter um programa de cashback de 2% em caça-níqueis. 98,5% + 2% = 100,5%.
Gostaria de acrescentar que, se você começar a jogar a estratégia de jackpot de 4000 moedas exatamente quando o jackpot atingir 7281,8, poderá esperar um lucro de 201,18 apostas. No entanto, se você dedicar um tempo para aprender as mudanças na estratégia para um jackpot de 7281,8 moedas, seu lucro esperado será de 234,31 moedas.
Aproveitando o assunto, acabei de ler "The Secret World of Video Poker Progressives" de Frank Kneeland. Este livro contém muitas fórmulas para situações progressivas bem mais complexas, além de conselhos práticos e histórias baseadas em seus anos à frente de uma equipe de caçadores de prêmios progressivos. Recomendo a leitura para jogadores de video poker progressivo com foco em vantagem competitiva.
Um cassino em Oklahoma está colocando três curingas em um sapato de blackjack com seis baralhos. Como isso afeta as probabilidades?
Stanford Wong aborda o uso de curingas no blackjack em seu livro "Basic Blackjack" . Nele, ele afirma que cada curinga por baralho vale 4,2% para o jogador. Portanto, meio curinga por baralho valeria 2,1%. Seu livro contém uma estratégia para determinar qual carta declarar como curinga, levando em consideração suas outras cartas e a carta aberta do dealer.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Existem pesquisas ou dados que detalhem a porcentagem de jogos de blackjack em Las Vegas que são 6-5 ou qualquer outra variação do tipo "carnaval"?
De acordo com a edição de setembro de 2010 do Current Blackjack Newsletter , havia 2099 mesas de blackjack em Las Vegas. A tabela a seguir mostra quantas eram de cada uma das quatro variações mais comuns.
Variantes de Blackjack em Las Vegas
| Jogo | Tabelas | Por cento |
| 6 a 5 | 467 | 22,2% |
| Blackjack Switch | 42 | 2,0% |
| Super Diversão 21 | 41 | 2,0% |
| Espanhol 21 | 6 | 0,3% |
| Total | 556 | 26,5% |
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .


