Pergunte ao Mago #261
Que dinâmicas afetam as apostas em totais no futebol à medida que a temporada avança, o clima piora e há mais informações sobre o desempenho recente das equipes? Quão fácil (ou difícil) é encontrar erros nas linhas de apostas?
Para ajudar a responder a essa pergunta, elaborei um gráfico com a média de pontos marcados por semana na NFL, com base em todas as temporadas de 1983 a 2009. O gráfico a seguir mostra os resultados.
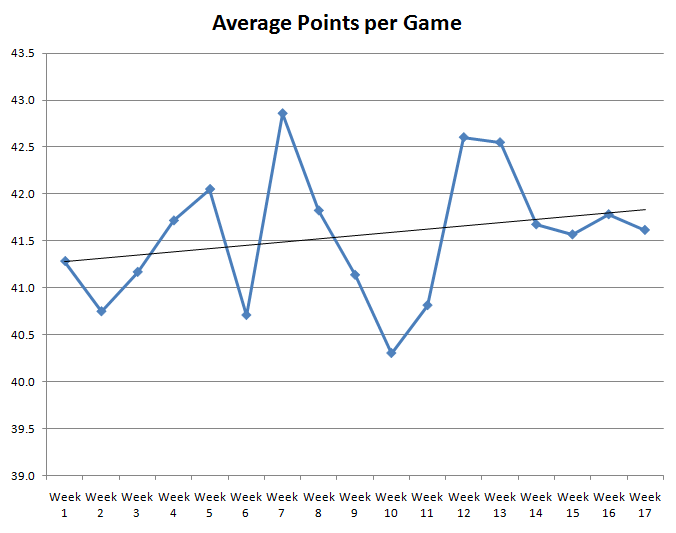
Como você pode ver, a linha oscila bastante. A linha preta fina é a linha de melhor ajuste por mínimos quadrados, que mostra uma tendência geral de alta. Portanto, conforme as estações avançam e as temperaturas caem, a média de pontos marcados aumenta ligeiramente, mas isso pode ser facilmente uma variação aleatória.
Isso é o máximo que posso dizer. Para uma opinião geral sobre como o clima afeta as apostas esportivas, recorri ao meu amigo Jason Been, que é especialista no assunto. Eis o que ele disse:
Na maioria dos casos, o vento é o principal fator climático que afeta um jogo; porém, não é o único. No beisebol e em outros esportes ao ar livre, as sombras podem ter um impacto semelhante, especialmente durante os jogos vespertinos do início e do fim da temporada. Chuva ou neve não são fatores tão relevantes no futebol americano quanto a maioria das pessoas pensa, pois geralmente afetam o ataque e a defesa igualmente. Um exemplo seria um defensor contra um recebedor. A chuva e a neve os atrasariam igualmente, não dando vantagem a nenhum dos lados. O vento pode simplesmente eliminar o jogo aéreo no futebol americano, assim como os chutes. Já vi jogos em que um time que priorizava o passe foi forçado a correr com a bola em quase todas as jogadas devido a um forte vento lateral. Não acontece com frequência, mas ocasionalmente o vento é o fator decisivo em uma partida.Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
O que normalmente acontece no craps se um jogador apostar um valor acima do multiplicador de probabilidades e os crupiês só perceberem isso quando a aposta for ganha ou perdida?
Perguntei a um ex-gerente de jogos de mesa de Las Vegas sobre isso. Ele disse que a parte da aposta de odds que excedesse o múltiplo permitido da aposta de linha seria paga com as odds da aposta de lugar. Essa questão foi levantada e discutida no fórum do meu site parceiro, Wizard of Vegas .
Na NFL, em média, qual é a probabilidade de que, após uma pontuação, o outro time seja o próximo a marcar?
Com base nas temporadas da NFL de 2000 a 2009, a resposta é 57%.
Considere um truel (um duelo triplo) com os participantes A, B e C. Eles estão lutando até a morte por uma mulher. Todos são cavalheiros e concordam com as seguintes regras.
- Os três participantes formam um triângulo.
- Cada um possui apenas uma bala.
- Primeiro vai A, depois B e, por último, C.
- A probabilidade de A atingir o alvo pretendido é de 10%.
- A probabilidade de B atingir o alvo pretendido é de 60%.
- A probabilidade de C acertar o alvo pretendido é de 90%.
- Não existem disparos acidentais.
- Atirar para o ar (errando de propósito) e atirar em si mesmo são permitidos e sempre dão certo.
- Se restarem dois ou três sobreviventes após qualquer rodada, cada um receberá uma nova bala. Eles então repetirão o processo, atirando alternadamente, na mesma ordem, ignorando qualquer um que já tenha morrido.
- Os três participantes são excelentes lógicos.
Em quem A deve mirar inicialmente? Qual é a probabilidade de sobrevivência dele para cada alvo inicial?
Este enigma é discutido no programa da BBC "Quite Interesting" . Desça 100 linhas para ver a resposta e a solução.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Aqui estão as minhas probabilidades de A vencer de acordo com cada alvo inicial. Como você pode ver, a probabilidade de A vencer é maximizada atirando deliberadamente para o ar.
Probabilidades Verdadeiras
| Estratégia | Prob. Vitória |
| Ar | 13,887% |
| UM | 0,000% |
| B | 12,560% |
| C | 13,094% |
Para a solução, vamos usar a notação Pr(X) para denotar a probabilidade de o grupo X, e somente o grupo X, permanecer após uma rodada. Vamos usar a terminologia Pr(X*) para denotar a probabilidade de o grupo X eventualmente vencer a rodada, após repetições até que o estado do jogo mude devido a alguém ser atingido. Seja Pr(X**) a probabilidade de o jogador X ser o único sobrevivente. Para encontrar as probabilidades finais, vamos analisar primeiro os estados com dois jogadores. É óbvio que cada um atirará no outro.
A vs. B
- Pr(A) = 0,1
- Pr(B) = 0,9 × 0,6 = 0,54
- Pr(AB) = 0,9 × 0,4 = 0,36
Se ambos sobreviverem, o processo se repetirá até que reste apenas um sobrevivente. Portanto, as probabilidades de ser o último sobrevivente são:
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0,1/0,64 = 0,15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0,54/0,64 = 0,84375
A vs. C
- Pr(A) = 0,1
- Pr(C) = 0,9×0,9 = 0,81
- Pr(AC) = 0,9×0,1 = 0,09
Se ambos sobreviverem, o processo se repetirá até que reste apenas um sobrevivente. Portanto, as probabilidades de ser o último sobrevivente são:
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0,1/0,91 = 0,10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0,81/0,91= 0,89010989
B vs. C
- Pr(B) = 0,6
- Pr(C) = 0,4 × 0,9 = 0,36
- Pr(BC) = 0,$×0,1 = 0,04
Se ambos sobreviverem, o processo se repetirá até que reste apenas um sobrevivente. Portanto, as probabilidades de ser o último sobrevivente são:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0,6/0,96 = 0,625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0,36/0,96= 0,375
Agora estamos prontos para analisar o caso com três jogadores. Vamos considerar a situação em que A tem como alvo B.
Três jogadores — A mira em B
Se A atingir B, então C certamente sobreviverá e poderá ou não atingir A. Portanto, dois resultados possíveis de atingir B são AC e C. Se A errar B, então B mirará na ameaça maior, C. Se B atingir C, então A e B sobreviverão. Se B errar C, então C mirará na ameaça maior, B. Se C errar B, então todos os três sobreviverão. Se C atingir B, então A e C sobreviverão. Portanto, os resultados possíveis são C, AB, AC e ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0,1 × 0,9 = 0,09. Isso é alcançado por A atingindo B e, em seguida, C atingindo A.
- Pr(AB) = 0,9 × 0,6 = 0,54. Isso é conseguido por A não atingir B e, em seguida, B atingir C.
- Pr(AC) = 0,1 × 0,1 + 0,9 × 0,4 × 0,9 = 0,334. Isso pode ser alcançado de duas maneiras. A primeira é A acertando B e, em seguida, C errando A. A segunda é A errando B, B errando C e, em seguida, C acertando B.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Isso é alcançado por todos os três elementos faltantes.
Pela mesma lógica dos casos de dois jogadores, podemos dividir cada resultado por (1-Pr(ABC))=0,964 para encontrar as probabilidades de cada estado, assumindo que o estado do jogo mudou após a rodada.
- Pr(C*) = 0,09/0,964 = 0,093361.
- Pr(AB*) = 0,54/0,964 = 0,560166.
- Pr(AC*) = 0,334/0,964 = 0,346473.
Nos casos com dois jogadores, sabemos que se restarem apenas A e B, A vencerá com probabilidade de 0,15625 e B com probabilidade de 0,84375. Se restarem apenas A e C, A vencerá com probabilidade de 0,109890 e C com probabilidade de 0,890110.
- Pr(A**) = (0,560165975 × 0,15625) + (0,346473029 × 0,10989011) = 0,125600. A pode ser o vencedor de duas maneiras: (1) chegando ao estado AB e então vencendo, ou (2) chegando ao estado AC e então vencendo.
- Pr(B**) = 0,560166 × 0,84375 = 0,472640. B será o vencedor se chegar ao estado AB, e então B vence.
- Pr(C**) = 0,093361 + (0,346473 × 0,890110) = 0,401760. C pode vencer se A matar B e depois C matar A na primeira rodada, ou se chegar ao estado AC e então C vencer.
Assim, se a estratégia de A for atacar B primeiro, sua probabilidade de ser o único sobrevivente é de 12,56%.
Três jogadores — A mira em C
Se A atingir C, então B certamente sobreviverá e poderá ou não atingir A. Portanto, dois resultados possíveis ao atingir C são AB e B. Se A errar C, então B mirará na ameaça maior, C. Se B atingir C, então A e B sobreviverão. Se B errar C, então C mirará na ameaça maior, B. Se C errar B, então os três sobreviverão. Se C atingir B, então A e C sobreviverão. Assim, os resultados possíveis são B, AB, AC e ABC.
- Pr(A) = 0.
- Pr(B) = 0,1 × 0,6 = 0,06.
- Pr(C) = 0.
- Pr(AB) = (0,1 × 0,4) + (0,9 × 0,6) = 0,04 + 0,54 = 0,58. Isso pode ser obtido de duas maneiras.A primeira situação é A acertando C e, em seguida, B errando A. A segunda situação é A errando B e, em seguida, B acertando C.
- Pr(AC) = 0,9 × 0,4 × 0,9 = 0,324. Isso é alcançado por A errando C, B errando C e C atingindo B.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Isso é alcançado por todos os três elementos faltantes.
Pela mesma lógica dos casos de dois jogadores, podemos dividir cada resultado por (1-Pr(ABC))=0,964 para encontrar as probabilidades de cada estado, assumindo que o estado do jogo mudou após a rodada.
- Pr(B*) = 0,06/0,964 = 0,062241.
- Pr(AB*) = 0,58/0,964 = 0,601660.
- Pr(AC*) = 0,324/0,964 = 0,336100.
Seguindo a mesma lógica da solução para o caso A visa B:
- Pr(A**) = (0,601660 × 0,15625) + (0,336100 × 0,10989011) = 0,130943.
- Pr(B**) = 0,062241 + 0,601660 × 0,84375 = 0,569891.
- Pr(C**) = 0,336100 × 0,890110 = 0,299166.
Assim, se a estratégia de A for atacar C primeiro, sua probabilidade de ser o único sobrevivente é de 13,09%.
Três jogadores — A erra deliberadamente
Após A errar deliberadamente o alvo, B mirará na ameaça maior, C. Se B acertar C, A e B sobreviverão. Se B errar C, C mirará na ameaça maior, B. Se C errar B, os três sobreviverão. Se C acertar B, A e C sobreviverão. Portanto, os resultados possíveis são AB, AC e ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.
- Pr(AB) = 0,6. Isso é conseguido quando B atinge C.
- Pr(AC) = 0,4 × 0,9 = 0,36. Isso é conseguido por B errar C e então C atingir B.
- Pr(BC) = 0.
- Pr(ABC) = 0,4 × 0,1 = 0,04. Isso é alcançado por todos os três elementos ausentes.
Pela mesma lógica dos casos de dois jogadores, podemos dividir cada resultado por (1-Pr(ABC))=0,96 para encontrar as probabilidades de cada estado, assumindo que o estado do jogo mudou após a rodada.
- Pr(AB*) = 0,6/0,96 = 0,625.
- Pr(AC*) = 0,36/0,96 = 0,375.
Seguindo a mesma lógica da solução para o caso A visa B:
- Pr(A**) = (0,625 × 0,15625) + (0,375 × 0,109890) = 0,138865.
- Pr(B**) = 0,625 × 0,84375 = 0,527344.
- Pr(C**) = 0,375 × 0,890110 = 0,333791.
Assim, se a estratégia de A for atacar C primeiro, sua probabilidade de ser o único sobrevivente é de 13,89%.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .


