Pergunte ao Mago #265

Você está confundindo a média com a mediana. Vejamos meu caso como exemplo. Sou um homem de 45 anos. Minha expectativa de vida é de 78,11 anos, mas tenho 50,04% de chance de chegar aos 80 anos.

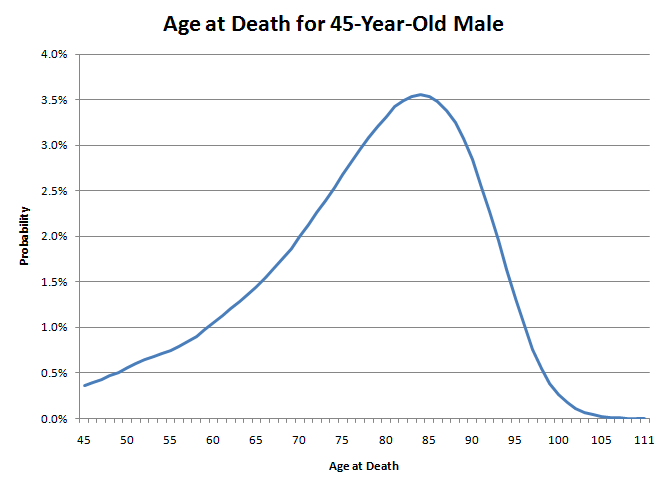
Minha idade de morte será como jogar um dardo neste gráfico. Observe como a cauda esquerda é muito mais espessa que a direita. Isso significa que minha probabilidade de morrer agora é bastante baixa. No entanto, à medida que envelheço, a probabilidade de morrer no próximo ano continuará aumentando. Por exemplo, para um homem de 45 anos, a probabilidade de sobreviver até os 46 é bastante alta, de 99,64%. No entanto, aos 85 anos, a probabilidade de chegar aos 86 é de apenas 89,21%. É como se a natureza estivesse lentamente enfiando uma faca nas suas costas. No início, provavelmente não vai te matar, mas a cada ano que passa, as chances de que isso aconteça aumentam gradualmente. Contudo, quando você chega perto dos setenta anos, a natureza diz chega de brincadeiras e começa a enfiar a faca nas suas costas de verdade.

Portanto, se muitos homens de 45 anos jogassem dardos neste gráfico, 49,96% acertariam entre 45 e 79 anos, e 50,04% acertariam entre 80 e 111 anos. No entanto, a metade sortuda que acerta o lado direito do gráfico provavelmente não viverá muito além dos 80 anos. Depois que um homem chega aos 80 anos, ele pode esperar viver apenas mais 7,78 anos. Enquanto isso, muitos na metade azarada que não chegam aos 80 anos morrerão muito mais jovens. Assim, são as muitas mortes precoces que reduzem a expectativa média de vida.

Para uma situação semelhante, considere um dado numerado 10, 20, 30, 31, 32, 33. A média é 26, mas há 2/3 de chance de rolar um número maior que esse.

Como exemplo da diferença entre média e mediana, suponha que adicionemos mais duas mortes à amostra. Uma morte aos 46 anos e outra aos 81. A probabilidade de chegar aos 80 anos não se altera, mas a expectativa média de vida aos 45 anos diminuiria.

Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .

Boa pergunta. A regra da casa diz para dividir cinco ases, jogando dois ases na mão baixa. A exceção é manter a quina na mão alta se você puder jogar dois reis na mão baixa. Minha página sobre pai gow poker indica sete regras da casa de Las Vegas e Atlantic City, e todas elas incluem essa exceção. As três regras de fora dessas duas cidades não a incluem.

A probabilidade de obter quatro ases, o curinga e dois reis é de 1 em 25.690.513. Supondo que o crupiê esteja bancando, a única situação em que essa exceção seria útil é se o jogador tivesse uma quadra ou uma mão melhor na mão alta. A probabilidade disso acontecer é de cerca de 1 em 300. A probabilidade de ambos os cenários ocorrerem é de cerca de 1 em 7,6 bilhões.

Segundo o Conselho de Controle de Jogos de Nevada, havia 306 mesas de pôquer pai gow em Nevada em 2009. Se assumirmos, generosamente, 60 mãos por hora, dois jogadores por mesa e que todas as mesas estão abertas 24 horas por dia, 7 dias por semana, então seriam necessários 23,7 anos para que essa exceção ocorresse e fizesse diferença no resultado.

Então, os cassinos estão exigindo que todos os crupiês de pai gow poker memorizem essa exceção, mesmo que ela nunca tenha feito diferença no resultado ao longo da história do jogo. Eu especulo que a mesma pessoa que pensou em adicionar essa regra foi a mesma que decidiu que a sequência A2345, conhecida como "a roda", é a segunda sequência mais alta.

Esse é um problema clássico na história do campo da probabilidade. Muitas pessoas pensam erroneamente que a resposta é 18, porque a probabilidade de sair um 12 é 1 em 36, e 18 × (1/36) = 50%. No entanto, por essa lógica, a probabilidade de se obter um 12 em 36 lançamentos seria de 100%, o que claramente não é o caso. Aqui está a solução correta. Seja r o número de lançamentos. A probabilidade de um lançamento não ser um 12 é 35/36. A probabilidade de haver 0 12s em r lançamentos é (35/36) ^r . Portanto, precisamos resolver para r na seguinte equação:

(35/36) ^r = 0,5
log(35/36) ^r = log(0,5)
r × log(35/36) = log(0,5)
r = log(0,5)/log(35/36)
r = 24,6051

Portanto, não há uma resposta arredondada. A probabilidade de tirar um 12 em 24 lançamentos é 1 - (35/36) ²⁴ = 49,14%. A probabilidade de tirar um 12 em 25 lançamentos é 1 - (35/36) ²⁵ = 50,55%.

Se você quiser apostar nisso, imagine que você consegue tirar um 12 em 25 lançamentos de dado, ou que outra pessoa não consegue em 24 lançamentos. De qualquer forma, você terá uma vantagem com odds de 1 para 1.

Eu apostaria 10 para 1 que você receberá o pagamento, embora eles possam ter algumas palavras com você antes. O motivo da minha dúvida é que uma casa de apostas pode cancelar uma aposta que foi obviamente feita por engano, com a permissão do Conselho de Controle de Jogos.

"Uma casa de apostas não pode rescindir unilateralmente qualquer aposta sem a prévia aprovação por escrito do presidente." -- Regulamento de Nevada 22.115

Embora esse direito exista, com base em relatos, ele raramente é invocado. Me avise o que acontecer.

P.S.: Mais tarde, a pessoa que fez a pergunta me informou que o pagamento foi efetuado sem maiores problemas.

Sim, irá, após e ^100.000 -1 segundos. Veja meu site mathproblems.info , problema 206, para duas soluções.

Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .