Pergunte ao Mago #267
Qual seria a estratégia ideal para dividir seu dinheiro no programa de jogos Million Dollar Money Drop, se você não tivesse certeza da resposta?
Para benefício dos demais leitores, permitam-me revisar as regras primeiro.
- Uma equipe de jogadores começa com US$ 1.000.000.
- A equipe recebe uma questão de múltipla escolha.
- A equipe deve dividir o dinheiro dele entre as possíveis respostas. O valor apostado na resposta correta avançará para a próxima pergunta.
- A equipe deve descartar completamente pelo menos uma resposta possível, não apostando dinheiro nela.
- Esse processo se repete por várias rodadas. O jogador também tem uma chance de mudar de ideia.
Obviamente, se a equipe tem certeza da resposta, ele deve apostar tudo na resposta correta. Se a equipe conseguir reduzir a resposta a duas, mas atribuir a cada uma 50% de chance de estar correta, então eles devem dividir o dinheiro dele igualmente entre as duas opções.
A situação se complica quando a equipe tende a escolher uma resposta, mas não descarta completamente uma ou mais das outras. Vejamos um exemplo. Suponha que a equipe determine a probabilidade de cada resposta correta da seguinte forma: A 10%, B 20%, C 30%, D 40%. Como eles deveriam dividir o dinheiro dele?
Afirmo que a resposta é seguir o Critério de Kelly . Resumidamente, a equipe deve maximizar o logaritmo de sua riqueza a cada pergunta. Para isso, é preciso considerar quanta riqueza já se possui.
Digamos que sua riqueza atual, acumulada independentemente do programa, seja de US$ 100.000. Esta é a sua primeira pergunta, então você tem US$ 1.000.000 do dinheiro do programa para dividir. Primeiro, elimine a opção com a menor probabilidade, para cumprir as regras do programa. Em seguida, você quer maximizar 0,2 × log(100.000 + b * 1.000.000) + 0,3 × log(100.000 + c * 1.000.000) + 0,4 × log(100.000 + d * 1.000.000), onde a, b e c em minúsculas se referem à porcentagem atribuída a cada resposta.
Isso pode ser resolvido com cálculo e a resolução de uma equação trinomial, por tentativa e erro ou, minha preferência, usando a função "atingir meta" do Excel. Seja qual for o método escolhido, a resposta correta é atribuir 18,9% à alternativa B, 33,3% à C e 47,8% à D.
É claro que ninguém no programa conseguirá fazer todos esses cálculos no tempo disponível, sem mencionar que também é preciso movimentar uma grande quantidade de dinheiro nesse período. Meu conselho mais prático é simplesmente dividir o dinheiro proporcionalmente à sua avaliação da probabilidade de a resposta estar correta, assumindo que a opção menos provável não seja uma possibilidade. No exemplo, isso resultaria em uma divisão de 22,2% para a opção B, 33,3% para a C e 44,4% para a D.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Ouvi falar de um cassino onde, se o crupiê estourar, ele assume que todos os jogadores restantes ganharam. As cartas são distribuídas com a face para cima, exceto as cartas de dobrar, que são distribuídas com a face para baixo. Então, se a carta de dobrar fizer o jogador estourar, mas o crupiê também estourar, o jogador ganha. O cassino faz isso porque tem receio de que os jogadores contem cartas e não quer que eles vejam cartas que considerem irrelevantes. Qual seria a estratégia básica correta sob essa regra e qual seria a vantagem da casa?
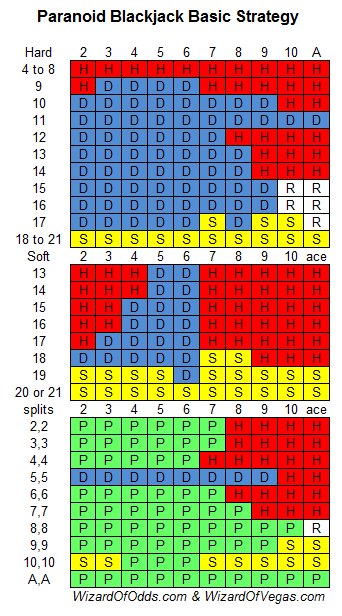
Vou assumir seis baralhos, o dealer pede carta com um 17 suave, dobra após dividir, desiste e divide os ases novamente. Se dobrar por menos não for permitido, então tenho uma vantagem do jogador de 4,9%. Esta é a estratégia correta. Obviamente, esta estratégia pode levantar algumas suspeitas.
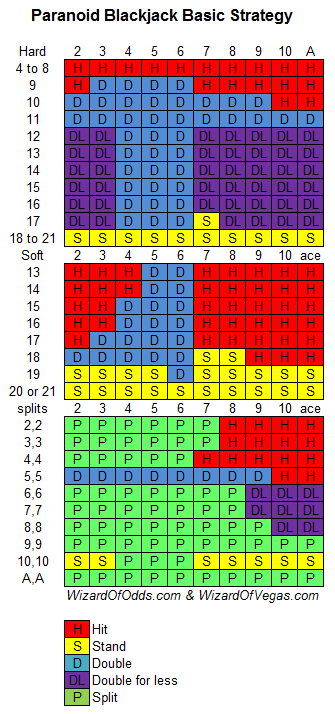
Se dobrar a aposta com um valor menor for permitido, então consigo uma vantagem máxima do jogador de 9,4% com a seguinte estratégia. Ao dobrar a aposta com um valor menor, aposte o mínimo possível a mais, de preferência apenas um centavo. Meu cálculo de 9,4% pressupõe uma aposta dobrada muito pequena. Na realidade, a maioria dos cassinos exige que a aposta dobrada seja feita com pelo menos o valor mínimo da mesa.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
No Casino Vienna, existe uma aposta paralela no blackjack. O jogo utiliza seis baralhos e o dealer para no 17 suave. Essa aposta paga 5 para 2 se o dealer ultrapassar 17, independentemente do resultado da aposta original.
Meu apêndice 2B sobre blackjack foi criado para perguntas como essa. Ele mostra que a probabilidade do dealer estourar é de 28,19% sob essas regras. Isso resultaria em uma vantagem da casa de 1,33%.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Em sua coluna de 14 de dezembro de 2010, você escreveu que a mão AAAAAKK, que é especificamente mencionada na descrição das regras da casa, pode nunca ter ocorrido na história do jogo. De acordo com outro crupiê, um jogador recebeu essa mão no Main Street Station em novembro de 2010.
Interessante. Como escrevi, estimo que essa mão ocorra aproximadamente uma vez a cada 23,7 anos em qualquer lugar de Nevada. Diria que essa foi uma dessas vezes.


