Pergunte ao Mago #270

Demonstro que o valor da divisão infinita, em comparação com a divisão em até quatro mãos, é de 0,05% se a regra se aplicar a todos os pares, incluindo ases, e de 0,02% se não incluir ases. Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .

Vejo que na Pinnacle as odds para a VCU ganhar o campeonato são: Sim +604 Não -750. Vamos calcular quanto você teria que apostar contra a VCU para garantir um resultado igual para ambos os lados, e qual seria esse resultado. Seja x o valor da aposta. Resultado da vitória = 50.000 - x
Resultado negativo = x*(100/750) = (2/15)x Igualando esses valores: 50000 - x = (2/15)x 50000 = (17/15)xx = 50000 × (15/17) x = $44.117,65 Vamos verificar se está correto... Se a VCU vencer, o resultado será de $50.000 menos o prêmio do Hilton menos $44.117,65 para a Pinnacle = $5.882,35. Se a VCU não vencer, você não recebe nada do Hilton, mas a aposta na Pinnacle pagará $44.117,65 × (100/750) = $5.882,35. No entanto, duvido que a aposta contra a VCU pague probabilidades justas. Se o dono fosse extremamente avesso ao risco e estivesse ansioso para vender o bilhete, então acho que cerca de $6.000 seria um valor justo. No entanto, eu basearia a probabilidade de vitória da VCU na linha de +604, que implica uma chance de 100/704 = 14,2%. Isso tornaria o valor do bilhete em torno de US$ 7.100. Tudo isso ignora as implicações fiscais. Essa questão foi levantada e discutida no fórum do meu site parceiro, Wizard of Vegas .

Não parece haver nenhuma mão imbatível quando não se está bancando. Então, vamos considerar duas mãos. A primeira não pode ser derrotada nem empatada na mão alta. A segunda não pode ser derrotada nem empatada na mão baixa.

(1) AAAAW/KK (W=selvagem)

Os cinco ases não podem ser batidos na mão alta, mas o par de reis pode ser empatado na mão baixa. O número de combinações com dois reis é combin (44,5) = 1.086.008. O número total de combinações de 7 cartas dentre as 46 restantes é 53.524.680. Portanto, a probabilidade de dois reis é 1.086.008/53.524.680 = 2,03%. Em muitas dessas combinações, o dealer não jogará o KK na mão baixa. De acordo com o meu Apêndice 1 de Pai Gow Poker , o dealer terá um par de ases ou menos na mão alta em 74,93% das vezes. Isso significa que ele fará um par duplo ou melhor, permitindo-lhe jogar os reis na mão baixa, em 25,07% das vezes. Assim, a probabilidade de o jogador receber dois reis e poder jogá-los na mão baixa é de 2,03% × 25,07% = 0,51%, ou 1 em 196.

(2) AWQJT (adequado)/AA

O Royal Flush pode ser empatado na mão alta, mas os ases não podem ser batidos ou empatados na mão baixa. Aqui, estou usando o curinga para substituir um rei e formar um Royal Flush, mas ele também poderia substituir a Dama, o Valete ou o Valete. Não quero que ele substitua um ás, porque então sobrariam dois ases no baralho para o crupiê empatar a mão baixa. Dessa forma, o crupiê só pode empatar a mão alta com outro Royal Flush. Qual a probabilidade disso? Restam três naipes para o Royal Flush, e as outras duas cartas podem ser de qualquer tipo. Portanto, o número de combinações que resultam em empate é 3 × combin(41,2) = 2.460. Obtenho o 41 das 46 cartas restantes no baralho depois que o jogador removeu 7 das 43 originais, e então subtraio mais 5 pelas 5 cartas do Royal Flush do crupiê. Temos combin(46,7) = 53.524.680 no denominador. Assim, a probabilidade de um empate com o curinga real/AA é de 2.460/53.524.680 = 0,004596%, ou 1 em 21.758.

Antes que algum perfeccionista me escreva, pode haver algumas situações bizarras em que o dealer não jogue a mão da maneira que eu planejei. Não estou buscando uma probabilidade exata para cada situação, mas sim fundamentar por que acredito que um Royal Flush/AA é a melhor mão que você pode obter no Pai Gow Poker quando não está bancando.

Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .

1/2.

Se usássemos o jogo de keno como comparação, cada pessoa teria 40 genes, cada um representado por uma bola de keno. No entanto, cada bola teria um número único. Quando duas pessoas, que não são parentes, se acasalam, é como combinar 80 bolas entre as duas em uma caçamba e escolher aleatoriamente 40 genes para a prole desse acasalamento.

Então, quando você foi concebido(a), metade das bolas que estavam no pote foram suas, e a outra metade foi descartada. Quando seu irmão ou irmã foi concebido(a), ele/ela recebeu metade das bolas sorteadas quando você nasceu e metade das bolas que não foram sorteadas. Portanto, vocês são 50% geneticamente idênticos. Isso ocorre pelo mesmo motivo que, se 40 números fossem sorteados no keno, dois sorteios consecutivos teriam, em média, 20 bolas em comum.

Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .

Vamos considerar c como o número de cadeiras produzidas por hora e t como o número de mesas. A receita por hora será de 10 × c + 20 × t.

As 10 serras resultam em 600 minutos de serragem por hora. Foi-nos informado que uma cadeira leva 10 minutos de serragem e uma mesa, 5. Isso limita a produção horária a:

(1) 10c + 5t <= 600

Os 6 tornos resultam em 360 minutos de torneamento por hora. Foi-nos informado que uma cadeira leva 5 minutos de serragem e uma mesa, 5 minutos. Isso limita a produção horária a:

(2) 5c + 5t <= 360

As 18 lixadeiras resultam em 1080 minutos de lixamento por hora. Foi-nos informado que uma cadeira leva 5 minutos de serragem e uma mesa, 20 minutos. Isso limita a produção horária a:

(3) 5c + 20t <= 1080

O gráfico a seguir mostra as três restrições impostas pelos três conjuntos de máquinas. A fábrica pode produzir qualquer combinação de cadeiras e mesas que esteja sob as três linhas de produção. A questão é: qual dessas três linhas resulta na maior receita?

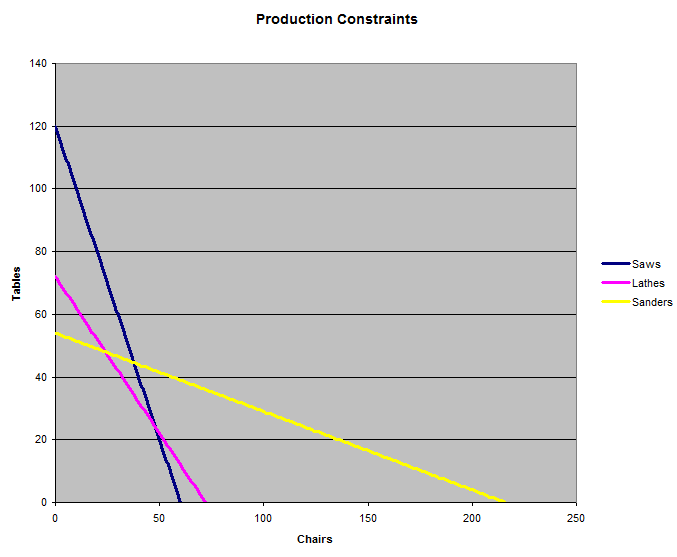
É lógico supor que a resposta seria a intersecção de duas retas, que formariam todas as cadeiras ou todas as mesas. Então, vamos encontrar onde as retas se intersectam. Primeiro, vamos encontrar onde as equações (1) e (2) se intersectam. Podemos substituir a expressão <= por apenas =, para aproveitar ao máximo o potencial das máquinas.

(1) 10c + 5t = 600
(2) 5c + 5t = 360

Subtraia (2) de (1):

5c = 240
c = 48

Substituindo 48 por c na equação (1):

10×48 + 5t = 600
5t = 120
t = 24

Assim, as equações (1) e (2) se encontram em 48 cadeiras e 24 mesas.

Em seguida, vamos encontrar o ponto de encontro das equações (2) e (3):

(2) 5c + 5t = 360
(3) 5c + 20t = 1080

Subtraindo (2) de (3):

15t = 720
t = 48

Colocando isso em (2) ou (3) podemos resolver para c, que é 24.

Assim, as equações (2) e (3) se encontram em 24 cadeiras e 48 mesas.

Não precisamos nos preocupar em encontrar onde as equações (1) e (3) se encontram, porque podemos ver pelo gráfico que onde as linhas da serra e da lixadeira se encontram está fora da restrição do torno.

Também é possível que fabricar apenas cadeiras seja a resposta correta. O gráfico mostra que as serras são a maior limitação para a fabricação exclusiva de cadeiras. A partir da equação (1), se substituirmos o número de mesas por 0, obtemos c = 60.

Outra possibilidade é fazer apenas mesas. O gráfico mostra que as lixadeiras serão a maior limitação. Colocando 0 cadeiras na equação (3), descobrimos que podemos fazer no máximo 54 mesas.

O gráfico a seguir mostra a receita total para cada resposta viável. Lembre-se, a receita é de US$ 10 por cadeira e US$ 20 por mesa.

Receita horária total

Cadeiras	Tabelas	Receita
0	54	$ 1.080
24	48	$ 1.200
48	24	$ 960
60	0	$ 600

Assim, a receita máxima possível é de US$ 1.200, obtida com a produção de 24 cadeiras e 48 mesas. Observe que isso deixaria algumas serras ociosas em alguns momentos. Essa questão também é levantada e discutida no fórum do meu site parceiro MathProblems.info , problema nº 28.