Pergunte ao Mago #293
Sei que em algumas mãos de vídeo poker existem situações em que duas jogadas são igualmente boas, sendo a melhor jogada possível. Por exemplo, com um dois pares em um par de dois curingas com pagamento integral, o jogador deve manter apenas um par, independentemente de qual seja. Minha pergunta é se existem situações em que três jogadas são igualmente boas, sendo a jogada correta?
Sim! No poker com curinga , com uma mão ruim, como regra geral é melhor manter uma das cartas do meio que tenha as melhores chances de formar uma sequência ou um flush. No entanto, às vezes é uma decisão difícil, ou até mesmo um empate, sobre qual é a melhor carta para se manter.
Por exemplo, na tabela de pagamento de 97,19% para dois pares com curinga no poker e uma Qh, 10d, 5d, 7c e 2c no draw, a melhor jogada é um empate entre segurar apenas o 10d, o 5d e o 7c, com um valor esperado de 0,240703 para as três cartas. Isso pode ser verificado usando meu analisador de mãos de vídeo poker .
Aqui estão outras jogadas semelhantes para a mesma tabela de pagamentos do joker poker:
- QC 10S 5D 7H 2C
- QH 10D 5D 7H 2C
- KH 10D 5D 8C 3C
- KC 10S 5D 8H 3C
- KH 10D 5D 8H 3C
Meus agradecimentos a Gary Koehler pela ajuda com esta questão.
Qual a sua opinião sobre como as novas regras para o ponto após um touchdown afetarão as apostas múltiplas de meio ponto ?
Para benefício de outros leitores, um dos meus truques é aproveitar os meio pontos extras em apostas combinadas de 3 e 7 pontos. Já demonstrei que essa é uma jogada vantajosa confiável, embora muito volátil.
A nova regra recua o chute extra para a linha de 15 jardas. Isso deve diminuir a probabilidade de sucesso do chute e induzir mais tentativas de conversão de dois pontos. Com mais tentativas de conversão de dois pontos, sejam elas bem-sucedidas ou não, não deve haver tantos jogos decididos por três ou sete pontos, diminuindo assim o valor de obter o meio ponto extra nesses números-chave em apostas múltiplas de meio ponto. Devemos nos preocupar? Vamos ver.
Em primeiro lugar, devemos nos preocupar, mas não necessariamente por este motivo. Outras mudanças nas regras prejudicaram a agressividade da defesa, levando a jogos com placares mais altos. O gráfico a seguir mostra a média de pontos marcados por jogo em cada temporada, de 1994 a 2014.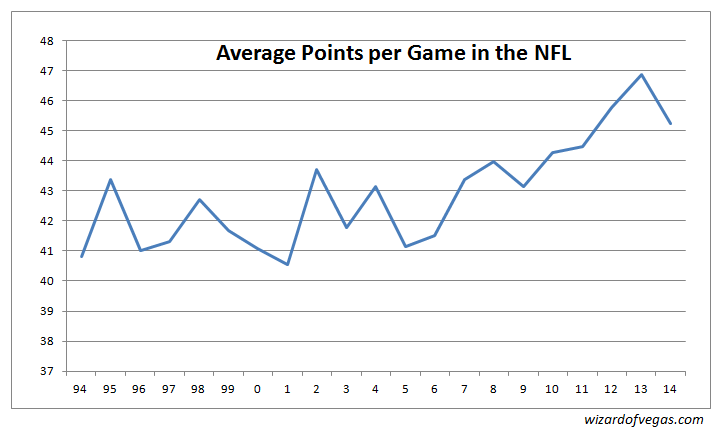
Como mostra o gráfico, a média de pontos por jogo manteve-se próxima de 42 até 2006. No entanto, a partir de 2007, a média vem aumentando em cerca de meio ponto por ano. Isso levanta a questão de se esse aumento na pontuação média tende a achatar a distribuição da margem de vitória, especialmente para os números mágicos de 3 e 7. O próximo gráfico mostra a probabilidade de uma margem de vitória de três e sete pontos por ano.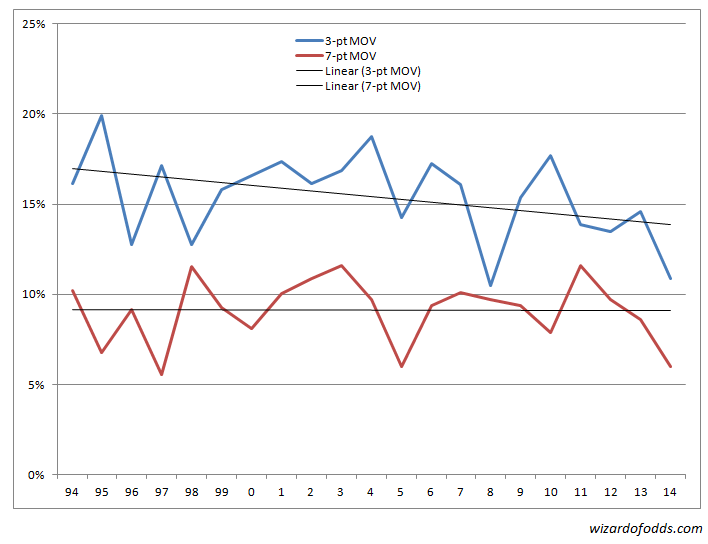
Como você pode ver, a probabilidade de uma vitória por sete pontos se mantém estável em 9,1%. No entanto, a probabilidade de uma vitória por três pontos vem diminuindo constantemente, especialmente desde 2004. Isso é ruim porque há muitas partidas com diferença de três pontos na NFL.
Independentemente da causa da diminuição das margens de vitória por três pontos, o valor das apostas combinadas de meio ponto está caindo. Será que a situação vai piorar ainda mais com a nova regra do ponto extra?
Minha resposta é que deveria doer, mas não muito. Antes da mudança na regra, calculo que cerca de 4,8% dos touchdowns eram seguidos por uma tentativa de conversão de dois pontos. Enquanto escrevo isto, ocorreram apenas duas semanas de jogos desde a mudança na regra. Nas duas primeiras semanas da temporada de 2015, houve 167 touchdowns e 15 foram seguidos por uma tentativa de conversão de dois pontos, resultando em uma taxa de tentativas de 9,0%.
Matematicamente falando, acho que tentar a conversão de dois pontos deveria ser muito mais comum, especialmente para times mais fracos que buscam variar o jogo, e não entendo por que não é. Não foi isso que você perguntou, mas eu precisava desabafar.
Digamos, por exemplo, que eu consiga acertar 54% das apostas contra o spread consistentemente. Para aumentar meu saldo o mais rápido possível, qual seria a opção mais lucrativa: apostar em acumuladas de três jogos com odds de 6 para 1?
Boa pergunta. Sua vantagem ao apostar contra 11 para 10 é de 3,09%, enquanto na aposta combinada é de 10,22%. Isso parece ser um ótimo argumento a favor da aposta combinada.
No entanto, lembre-se de que a estratégia ideal para aumentar a banca em qualquer jogo com vantagem é usar o Critério de Kelly . De acordo com Kelly, o tamanho ideal da aposta é aquele que maximiza o logaritmo esperado da banca após a aposta. Para apostas com apenas dois resultados possíveis, o tamanho ideal da aposta é, convenientemente, a vantagem dividida pelo pagamento da aposta em uma proporção de "um para um".
As apostas simples pagam de 10 a 11. Isso tornaria o tamanho ideal da aposta 0,030909/(10/11) = 0,034000. Com uma vantagem do jogador de 3,09%, você pode esperar ganhar 0,001051 vezes o seu saldo por jogo em apostas simples.
O tamanho ideal da aposta combinada é 0,102248/6 = 0,017041. Com uma vantagem do jogador de 0,102248, você pode esperar ganhar 0,001742 vezes o seu saldo por jogo apostando diretamente.
No entanto, as apostas simples são melhores porque permitem apostar três vezes. Portanto, multiplique o ganho esperado por aposta simples por três para obter 3 × 0,001051 = 0,003153. Isso representa um aumento de 81% em relação ao crescimento da banca em apostas múltiplas.
Se você tem um saldo tão grande que chega a atingir os limites máximos de apostas, provavelmente é melhor fazer primeiro uma aposta combinada, que geralmente não altera as linhas, e depois fazer suas apostas simples.
Essa questão é levantada e discutida no meu fórum no Wizard of Vegas .
Como você sabe, o ponto extra agora deve ser tentado da linha de 15 jardas na NFL, enquanto a tentativa de conversão de dois pontos permanece na linha de duas jardas. Você acha que isso muda o cálculo da decisão? Em outras palavras, qual é a jogada correta agora?
É uma decisão controversa, que acredito ser o objetivo da NFL ao alterar a regra. Alguns fatores a serem considerados na tomada de decisão são:
- Probabilidade de sucesso ao chutar.
- Probabilidade de sucesso ao tentar a conversão de dois pontos.
- Probabilidades gerais de vitória de cada equipe.
No final do jogo, também é crucial considerar os números-chave. Por exemplo, se estiver bem perto do fim e você acabou de marcar um touchdown, colocando seu time três pontos à frente, então você deve chutar. Se acertar, você estará quatro pontos à frente e forçará o outro time a marcar um touchdown para vencer. Se tentar a conversão de dois pontos e errar, o outro time pode empatar com apenas um field goal. Portanto, vou limitar minha discussão ao início do jogo, quando os números-chave não são um fator tão importante.
Para responder à sua pergunta, escrevi um programa de simulação. Embora seja um tanto rudimentar, acredito que ele reflita com bastante precisão a natureza da NFL em termos de field goals, touchdowns e turnovers.
De acordo com o artigo " Qual o efeito de mover os pontos extras para a linha de 15 jardas?" de Kevin Rudy, a probabilidade de converter o ponto extra a partir da linha de 15 jardas é de 94,2%. Inseri 94% no meu programa para manter os números arredondados.
Existe mais divergência quanto à probabilidade de conversão de dois pontos. Parece óbvio que isso também varia significativamente de acordo com a defesa e o ataque específicos. O que eu fiz foi executar simulações com taxas de sucesso de conversão de dois pontos entre 46% e 50%, em grupos de 1%.
Em cada simulação, eu fiz com que uma equipe sempre chutasse a bola e a adversária tentasse a conversão de dois pontos para cada probabilidade de sucesso. Também realizei simulações onde ambas as equipes sempre chutavam a bola, para ter um parâmetro de comparação para os resultados da conversão de dois pontos.
A Tabela 1 abaixo mostra os resultados de duas equipes com habilidades equivalentes. A equipe A sempre chuta a bola após um touchdown. A tabela mostra a probabilidade de vitória da equipe B e a média de pontos adicionais marcados por jogo, de acordo com a decisão da equipe B de chutar a bola ou tentar a conversão de dois pontos (2PC), bem como a probabilidade de sucesso dessa tentativa.
Tabela 1 — Equipes Iguais
| Equipe B Estratégia | Equipe B Provavelmente. Ganhar | Média Adicional Pontos |
|---|---|---|
| Chute | 50,00% | 0,0001 |
| 2PC -- 46% | 49,76% | 0,0491 |
| 2PC -- 47% | 49,90% | 0,0000 |
| 2PC -- 48% | 50,05% | 0,0492 |
| 2PC -- 49% | 50,19% | 0,0980 |
| 2 peças -- 50% | 50,33% | 0,1461 |
Note que, com uma probabilidade de sucesso de 47%, os pontos adicionais esperados são de 0,94, tanto para um chute quanto para uma conversão de dois pontos. No entanto, a probabilidade de vitória é 0,1% menor ao optar pela conversão de dois pontos. Acredito que isso se deva ao fato de que, se o chute for errado, o outro time tem a chance de empatar com dois field goals. É importante ressaltar que esse efeito numérico é bastante pequeno, mas favorece uma abordagem conservadora, optando pelo chute, considerando todas as outras variáveis iguais. Em resumo, com duas equipes de nível semelhante, a probabilidade de sucesso na conversão de dois pontos deve ser de pelo menos 49% para optar por ela.
A Tabela 2 abaixo mostra os resultados de duas equipes desiguais, onde a equipe A é mais forte. A equipe A sempre chuta a bola após um touchdown. Ela apresenta as mesmas estatísticas da Tabela 1 acima.
Tabela 2 — Equipe A Mais Forte
| Equipe B Estratégia | Equipe B Provavelmente. Ganhar | Média Adicional Pontos |
|---|---|---|
| Chute | 28,83% | -7,0039 |
| 2PC -- 46% | 29,01% | -7,0519 |
| 2PC -- 47% | 29,16% | -7,0039 |
| 2PC -- 48% | 29,30% | -6,9568 |
| 2PC -- 49% | 29,45% | -6,9083 |
| 2 peças -- 50% | 29,60% | -6,8595 |
A Tabela 2 mostra que a equipe mais fraca deve tentar a conversão de dois pontos em todas as probabilidades de sucesso listadas. Mesmo em 45%, onde o número esperado de pontos totais marcados é menor. Por que isso acontece, você pode perguntar. Isso ocorre porque, em qualquer jogo, a equipe mais fraca deve buscar a variação, enquanto a equipe mais forte deve evitá-la.
A Tabela 3 abaixo mostra os resultados de duas equipes desiguais, onde a equipe B é mais forte. A equipe A sempre chuta a bola após um touchdown. Ela mostra as mesmas estatísticas das Tabelas 1 e 2 acima.Tabela 3 — Equipe B Mais Forte
| Equipe B Estratégia | Equipe B Provavelmente. Ganhar | Média Adicional Pontos |
|---|---|---|
| Chute | 71,17% | 7,0042 |
| 2PC -- 46% | 70,53% | 6,9349 |
| 2PC -- 47% | 70,67% | 7.0030 |
| 2PC -- 48% | 70,82% | 7,0725 |
| 2PC -- 49% | 70,97% | 7.1412 |
| 2 peças -- 50% | 71,12% | 7.2109 |
Observe que a tabela 3 mostra uma probabilidade de vitória da equipe B igual a 71,17% por meio de um chute. Essa probabilidade é menor do que a de todas as outras probabilidades de sucesso apresentadas, mesmo que o número esperado de pontos seja maior com uma probabilidade de sucesso de 49% ou 50%. A razão, novamente, é que equipes mais fracas devem buscar a variação, enquanto as mais fortes devem evitá-la. A tentativa de conversão de dois pontos adiciona volatilidade ao jogo, e é por isso que equipes mais fracas, em igualdade de condições, tendem a ser mais propensas a tentar esse tipo de conversão do que equipes mais fortes.


