Recomendações do Mago
-
Bônus de boas-vindas de $11000 -
Bônus de boas-vindas de 3000 $ -
BÔNUS DE ATÉ $777
Pergunte ao Mago #301
Toda semana há um sorteio no cassino local, onde o vencedor recebe US$ 5.000 em dinheiro ou a opção de escolher uma sacola surpresa contendo um dos seguintes prêmios:
- US$ 2.000 em dinheiro
- Fichas no valor de US$ 4.000, não negociáveis.
- Fichas no valor de $6.000 (não negociáveis)
- US$ 8.000 em dinheiro
- US$ 10.000 em dinheiro
Qual você escolheria e por quê?
Primeiramente, presumo que as "fichas não negociáveis" sejam do tipo "use até perder". Estas têm um valor de cerca de 98% do seu valor nominal, dependendo das regras dos jogos em que podem ser usadas.
Dito isso, a bolsa custa em média US$ 5.960. Isso é quase 20% a mais do que a oferta em dinheiro. Mesmo considerando a utilidade do dinheiro, você ainda deveria aceitar a bolsa, mesmo que não tenha outros bens.
Essa pergunta foi feita e discutida no meu fórum no Wizard of Vegas .
Qual é o número médio de amostras necessárias de uma distribuição uniforme de 0 a 1 para que a soma seja igual a 1?
Qual era o problema de matemática escrito no quadro-negro no filme Gênio Indomável ?
Na verdade, foi bem fácil, especialmente para um curso de matemática combinatória no MIT. Eis o enunciado do problema:
"Desenhe todas as árvores homeomorficamente irredutíveis de tamanho n=10."
Aqui está minha tentativa de explicar isso em inglês simples e direto.
Usando apenas linhas retas, desenhe todas as figuras onde a soma das interseções e dos becos sem saída seja igual a 10. Não pode haver nenhum laço fechado. Também não pode haver duas figuras equivalentes. Qualquer interseção deve ter pelo menos três caminhos partindo dela.
O que quero dizer com "equivalente", você pode perguntar? Significa que você pode mover as peças, deixando as interseções intactas, da maneira que quiser, e isso não criará nenhuma figura nova.
Aqui está um exemplo: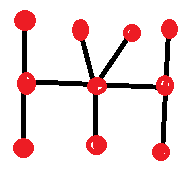
Vou dar uma dica. Ao contrário da resposta do filme, são dez. Will acertou apenas oito. Veja se você consegue igualar ou superar Will Hunting.
[spoiler]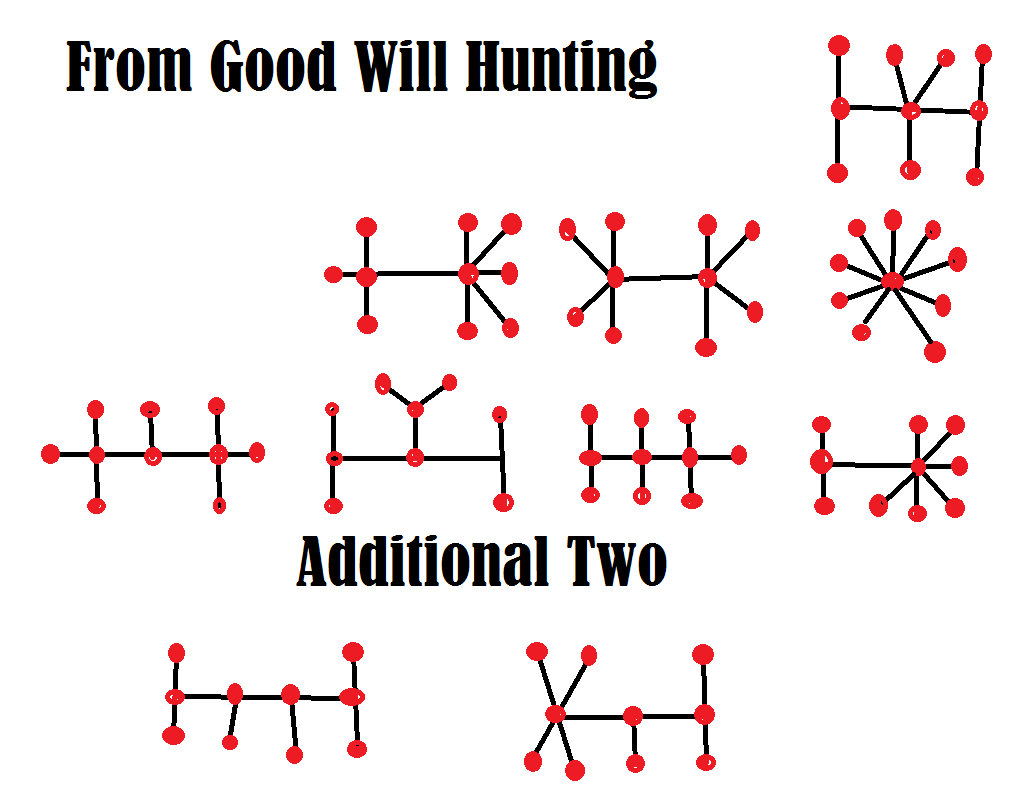
Apresento a minha lógica para chegar aos dez resultados no meu site MathProblems.info , problema 220.
[spoiler] Leitura complementar:- MATEMÁTICA EM GÊNIO INDOMÁVEL II: PROBLEMAS DA PERSPECTIVA DOS ALUNOS -- Artigo acadêmico sobre o problema.
- O PROBLEMA MATEMÁTICO DE "GÊNIO INDOMÁVEL" -- Discussão sobre o problema no meu fórum.
Em alguns cassinos do México, eles usam dados em vez de uma roda na roleta. Aqui estão as regras:
- Há quatro dados: dois verdes, um vermelho e um azul.
- Se os dois dados verdes caírem ambos no número um, o resultado da "giro" será zero.
- Se os dois dados verdes caírem ambos no número seis, o resultado da "giro" será um duplo zero.
- Se ocorrer qualquer outro resultado com o dado verde, os 36 resultados possíveis dos dados vermelho e azul serão mapeados para os números 1 e 36 para representar a "rotação".
Como isso altera as probabilidades em comparação com a roleta convencional?
A probabilidade de ganhar com 0 e 00 seria de 1/36 para cada. Se as apostas nesses resultados pagassem o valor usual de 35 para 1, então a vantagem da casa seria exatamente 0%.
A probabilidade de qualquer outro número ser vencedor seria (34/36)*(1/36) = 2,62%. Compare isso com 1/38 = 2,63% na roleta tradicional com duplo zero. A vantagem da casa em qualquer aposta nos números de 1 a 36 seria de 5,56%. Compare isso com os 5,26% na roleta tradicional com duplo zero. Meu conselho neste jogo seria apostar apenas no zero e no duplo zero.
Se alguém puder confirmar ou negar essas regras e pagamentos, por favor, me avise.