Pergunte ao Mago #307
Estou participando de um bolão de mortes de 2018. Aqui estão as regras:
- Cada jogador deve enviar uma lista de dez celebridades vivas com menos de 100 anos de idade.
- Se alguma celebridade falecer, conforme evidenciado por uma menção da Associated Press, em 2018, então qualquer pessoa que tenha o nome da celebridade em sua lista receberá 100-x pontos, onde x é a idade da celebridade no momento da morte.
- O jogador com mais pontos em 01/01/2019 vence.
Levando em conta as médias, qual é a estratégia ideal para este jogo?
Como ex-atuário, você perguntou à pessoa certa. Espero que a Sociedade de Atuários não considere minha resposta um abuso da profissão. Dito isso, para responder à sua pergunta, consultei uma Tabela de Mortalidade Periódica de 2014 do meu antigo local de trabalho, o Gabinete do Atuário-Chefe da Administração da Previdência Social.
Uma tábua de mortalidade periódica mostra, entre outras coisas, a probabilidade de morte para uma pessoa de qualquer idade e sexo em 2014. Usando essa informação, criei a seguinte tabela, que mostra tanto a probabilidade de morte quanto a expectativa de vida para todas as idades de 0 a 100 anos e ambos os sexos.
Tabela de Mortalidade do Período de 2014
| Idade | Probabilidade de Morte — Masculino | Probabilidade de Morte — Feminina | Esperado Pontos — Masculino | Esperado Pontos — Feminino |
|---|---|---|---|---|
| 0 | 0,006320 | 0,005310 | 0,632000 | 0,531000 |
| 1 | 0,000403 | 0,000352 | 0,039852 | 0,034835 |
| 2 | 0,000282 | 0,000221 | 0,027626 | 0,021683 |
| 3 | 0,000211 | 0,000161 | 0,020514 | 0,015612 |
| 4 | 0,000181 | 0,000131 | 0,017405 | 0,012556 |
| 5 | 0,000161 | 0,000111 | 0,015313 | 0,010515 |
| 6 | 0,000141 | 0,000111 | 0,013260 | 0,010405 |
| 7 | 0,000131 | 0,000101 | 0,012184 | 0,009360 |
| 8 | 0,000121 | 0,000091 | 0,011127 | 0,008334 |
| 9 | 0,000091 | 0,000081 | 0,008256 | 0,007328 |
| 10 | 0,000101 | 0,000091 | 0,009073 | 0,008154 |
| 11 | 0,000101 | 0,000081 | 0,008973 | 0,007168 |
| 12 | 0,000131 | 0,000101 | 0,011535 | 0,008861 |
| 13 | 0,000202 | 0,000131 | 0,017547 | 0,011389 |
| 14 | 0,000303 | 0,000151 | 0,026023 | 0,012992 |
| 15 | 0,000404 | 0,000191 | 0,034304 | 0,016267 |
| 16 | 0,000505 | 0,000232 | 0,042393 | 0,019464 |
| 17 | 0,000616 | 0,000272 | 0,051129 | 0,022582 |
| 18 | 0,000748 | 0,000302 | 0,061316 | 0,024796 |
| 19 | 0,000880 | 0,000343 | 0,071262 | 0,027768 |
| 20 | 0,001022 | 0,000373 | 0,081780 | 0,029855 |
| 21 | 0,001145 | 0,000404 | 0,090445 | 0,031884 |
| 22 | 0,001258 | 0,000444 | 0,098105 | 0,034643 |
| 23 | 0,001310 | 0,000475 | 0,100880 | 0,036546 |
| 24 | 0,001332 | 0,000495 | 0,101246 | 0,037625 |
| 25 | 0,001344 | 0,000526 | 0,100811 | 0,039422 |
| 26 | 0,001377 | 0,000556 | 0,101864 | 0,041162 |
| 27 | 0,001389 | 0,000577 | 0,101371 | 0,042106 |
| 28 | 0,001421 | 0,000608 | 0,102330 | 0,043740 |
| 29 | 0,001454 | 0,000648 | 0,103234 | 0,046036 |
| 30 | 0,001507 | 0,000669 | 0,105517 | 0,046837 |
| 31 | 0,001530 | 0,000710 | 0,105584 | 0,048998 |
| 32 | 0,001574 | 0,000751 | 0,107011 | 0,051084 |
| 33 | 0,001617 | 0,000813 | 0,108364 | 0,054454 |
| 34 | 0,001661 | 0,000864 | 0,109644 | 0,057041 |
| 35 | 0,001716 | 0,000926 | 0,111521 | 0,060194 |
| 36 | 0,001781 | 0.001008 | 0,113970 | 0,064538 |
| 37 | 0,001857 | 0,001081 | 0,116963 | 0,068090 |
| 38 | 0,001933 | 0,001164 | 0,119830 | 0,072145 |
| 39 | 0,002020 | 0,001237 | 0,123207 | 0,075427 |
| 40 | 0,002118 | 0,001340 | 0,127066 | 0,080422 |
| 41 | 0,002258 | 0,001445 | 0,133232 | 0,085232 |
| 42 | 0,002410 | 0,001560 | 0,139778 | 0,090455 |
| 43 | 0,002615 | 0,001696 | 0,149075 | 0,096649 |
| 44 | 0,002843 | 0,001853 | 0,159228 | 0,103761 |
| 45 | 0,003105 | 0,002011 | 0,170771 | 0,110606 |
| 46 | 0,003401 | 0,002191 | 0,183635 | 0,118300 |
| 47 | 0,003742 | 0,002403 | 0,198314 | 0,127342 |
| 48 | 0,004108 | 0,002647 | 0,213613 | 0,137656 |
| 49 | 0,004532 | 0,002894 | 0,231133 | 0,147577 |
| 50 | 0,004994 | 0,003194 | 0,249696 | 0,159718 |
| 51 | 0,005473 | 0,003487 | 0,268191 | 0,170880 |
| 52 | 0,005993 | 0,003794 | 0,287656 | 0,182103 |
| 53 | 0,006565 | 0,004104 | 0,308561 | 0,192871 |
| 54 | 0,007159 | 0,004428 | 0,329324 | 0,203676 |
| 55 | 0,007799 | 0,004767 | 0,350946 | 0,214498 |
| 56 | 0,008475 | 0,005153 | 0,372902 | 0,226729 |
| 57 | 0,009179 | 0,005534 | 0,394696 | 0,237972 |
| 58 | 0,009856 | 0,005889 | 0,413944 | 0,247347 |
| 59 | 0,010575 | 0,006272 | 0,433558 | 0,257150 |
| 60 | 0,011350 | 0,006683 | 0,453991 | 0,267338 |
| 61 | 0,012209 | 0,007180 | 0,476135 | 0,280016 |
| 62 | 0,013061 | 0,007720 | 0,496330 | 0,293355 |
| 63 | 0,013921 | 0,008339 | 0,515084 | 0,308537 |
| 64 | 0,014814 | 0,009029 | 0,533320 | 0,325041 |
| 65 | 0,015831 | 0,009839 | 0,554094 | 0,344371 |
| 66 | 0,016981 | 0,010741 | 0,577354 | 0,365197 |
| 67 | 0,018300 | 0,011752 | 0,603909 | 0,387812 |
| 68 | 0,019778 | 0,012879 | 0,632894 | 0,412117 |
| 69 | 0,021443 | 0,014142 | 0,664734 | 0,438397 |
| 70 | 0,023384 | 0,015613 | 0,701513 | 0,468376 |
| 71 | 0,025547 | 0,017271 | 0,740873 | 0,500852 |
| 72 | 0,027877 | 0,019047 | 0,780560 | 0,533320 |
| 73 | 0,030384 | 0,020918 | 0,820374 | 0,564797 |
| 74 | 0,033098 | 0,022938 | 0,860535 | 0,596385 |
| 75 | 0,036256 | 0,025299 | 0,906400 | 0,632465 |
| 76 | 0,039868 | 0,028043 | 0,956841 | 0,673035 |
| 77 | 0,043883 | 0,031127 | 1,009299 | 0,715914 |
| 78 | 0,048257 | 0,034590 | 1,061657 | 0,760984 |
| 79 | 0,053128 | 0,038456 | 1,115692 | 0,807583 |
| 80 | 0,058709 | 0,043007 | 1,174177 | 0,860145 |
| 81 | 0,065070 | 0,048186 | 1,236322 | 0,915536 |
| 82 | 0,072149 | 0,053762 | 1,298691 | 0,967712 |
| 83 | 0,079906 | 0,059769 | 1,358409 | 1,016065 |
| 84 | 0,088524 | 0,066380 | 1,416378 | 1,062085 |
| 85 | 0,098157 | 0.073823 | 1,472348 | 1,107351 |
| 86 | 0,108904 | 0,082381 | 1,524651 | 1,153334 |
| 87 | 0,120889 | 0,092180 | 1,571556 | 1,198344 |
| 88 | 0,134134 | 0,103305 | 1,609607 | 1,239664 |
| 89 | 0,148707 | 0,115744 | 1,635778 | 1,273180 |
| 90 | 0,164522 | 0,129477 | 1,645220 | 1,294772 |
| 91 | 0,181584 | 0,144435 | 1,634254 | 1,299911 |
| 92 | 0,199903 | 0,160621 | 1,599225 | 1,284970 |
| 93 | 0,219362 | 0,177816 | 1,535534 | 1,244713 |
| 94 | 0,239881 | 0,196194 | 1,439286 | 1,177165 |
| 95 | 0,260293 | 0,214694 | 1,301463 | 1,073469 |
| 96 | 0,280129 | 0,233056 | 1.120515 | 0,932225 |
| 97 | 0,299042 | 0,251152 | 0,897125 | 0,753456 |
| 98 | 0,316317 | 0,268235 | 0,632634 | 0,536471 |
| 99 | 0,332667 | 0,284442 | 0,332667 | 0,284442 |
| 100 | 0,348651 | 0,301417 | 0,000000 | 0,000000 |
A tabela mostra que a pontuação máxima esperada é de 1,645220 para um homem de 90 anos.
Essa questão é levantada e discutida no meu fórum não relacionado a jogos de azar, Diversity Tomorrow .
Registrei 7.456 giros na roleta. Os resultados são os seguintes. Suspeito que a roleta esteja viciada, mas não tenho certeza se os dados são conclusivos o suficiente para jogar.
Dados da Roleta
| Vencendo Número | ocorrências |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| Total | 7456 |
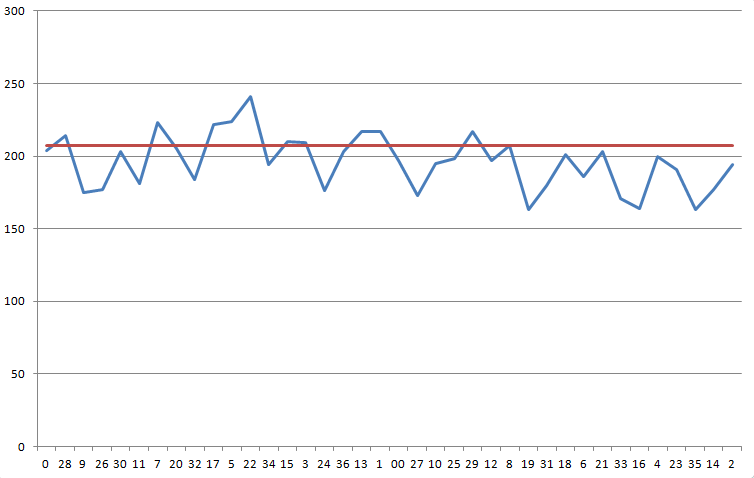
O gráfico a seguir mostra seus resultados em ordem sequencial na roleta. A linha azul mostra seus resultados. A linha vermelha representa o número que você precisa, 207,11, para superar a vantagem da casa de 5,26%.
Um teste qui-quadrado nessa distribuição retorna uma estatística de 68,1 com 37 graus de liberdade. A probabilidade de um resultado tão assimétrico ou mais é de 1 em 725.
Não creio que o teste qui-quadrado seja o ideal para esta situação, pois não considera a ordem dos resultados, mas desconheço um teste melhor. Alguns sugeriram o teste de Kolmogorov-Smirnov , mas não o considero apropriado. Se houver outros testes adequados, estou aberto a sugestões.
Posso afirmar que, se você tivesse apostado no arco de 3 números em torno do número 5, teria obtido um lucro de 10,57% nas rodadas registradas. No entanto, se aumentasse para um arco de 7 números, a vantagem cairia para 2,84%.
Se eu tivesse que dar uma resposta em linguagem simples e direta, diria que a roleta apresenta indícios, mas não provas irrefutáveis, de que é viciada. No entanto, esse viés provavelmente não é suficiente para superar de forma significativa e confiável a vantagem da casa. Supondo que o cassino não troque as roletas entre as mesas, eu diria que mais dados deveriam ser coletados antes de apostar grandes quantias de dinheiro. Lamento que esta resposta seja tão vaga.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Dois jogadores, Sam e Dan, possuem cinco moedas cada. Ambos devem escolher entre colocar de uma a cinco moedas em suas mãos. Ao mesmo tempo, cada um deve revelar o número de moedas jogadas. Se ambos escolherem o mesmo número de moedas, Sam ganhará e coletará todas as moedas jogadas. Se ambos escolherem números diferentes de moedas, Dan coletará todas as moedas jogadas. Supondo que ambos os jogadores sejam lógicos perfeitos, qual é a estratégia ótima para Dan?
Dan deve randomizar sua estratégia da seguinte forma:
- Probabilidade de escolher uma moeda = 77/548.
- Probabilidade de escolher uma moeda = 107/548.
- Probabilidade de escolher uma moeda = 117/548.
- Probabilidade de escolher uma moeda = 122/548.
- Probabilidade de escolher uma moeda = 125/548.
Com essa estratégia, Dan pode esperar ganhar 3,640510949 moedas a cada rodada, independentemente de quantas moedas Sam escolher.
A solução pode ser encontrada no meu site de Problemas de Matemática , problema 230.
Uma pergunta relacionada, que levou a esta, pode ser encontrada no meu fórum no Wizard of Vegas .
Existe um jogo de blackjack chamado Hot Action Blackjack sendo jogado no California Grand Casino em São Francisco. As regras do jogo são as seguintes:
- Seis baralhos em um embaralhador contínuo com 18 curingas adicionais com valor facial de 2.
- O revendedor atinge o nível 17 com relativa suavidade.
- Dobre o valor das suas duas primeiras cartas.
- Divida novamente até quatro mãos.
- Não é permitido trocar ou dividir ases novamente.
- Sem rendição.
- O Blackjack paga 6 para 5.
- Se as duas primeiras cartas do jogador forem curingas, ele recebe um bônus de 4 para 1.
- Se as duas primeiras cartas do jogador forem ases do mesmo naipe, ele recebe um bônus de 5 para 1.
- O jogador deve pagar uma comissão de 5% para jogar.
Qual é a estratégia básica e a vantagem da casa?
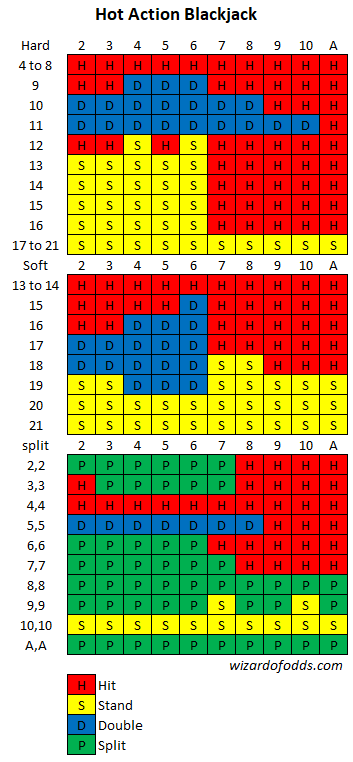
Primeiramente, aqui está minha estratégia básica de acordo com essas regras:
Considerando tudo, mostro uma vantagem da casa de 6,01% (ai!) com base na aposta inicial. Em outras palavras, se o jogador apostar US$ 100, sem contar a comissão de US$ 5, ele pode esperar perder US$ 6,01. Isso mostra por que eu evitaria jogos com banca de jogadores na Califórnia, a menos que você seja o banqueiro.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .