Pergunte ao Mago #313
Qual é a variância no Keno de Cleópatra?
Lembrando aos nossos leitores, o Cleopatra Keno funciona como o keno tradicional, com a diferença de que, se a última bola sorteada corresponder a uma das escolhas do jogador E resultar em uma vitória, o jogador também ganhará 12 rodadas grátis com um multiplicador de 2x. Rodadas grátis não geram mais rodadas grátis.
Você não especificou o número de escolhas nem a tabela de pagamento, então vamos usar a tabela de pagamento 3-10-56-180-1000 pick-8 como exemplo. Primeiro, vamos calcular o retorno.
O número de maneiras de pegar x bolas de y no keno é igual ao número de maneiras de escolher x bolas de 20 e yx de 60. Isso é igual a combin(20,x)*combin(60,yx), para usar uma analogia do Excel. Lembrando que combin(x,y) = x!/(y!*(xy)!). Portanto, x! = 1*2*3*...*x.
Feita essa revisão, aqui está a tabela de retorno para essa tabela de pagamentos. A coluna da direita mostra o quadrado esperado do ganho, que precisaremos mais tarde.
Escolha 8 Keno
| Evento | Paga | Combinações | Probabilidade | Retornar | Retorno^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2.558.620.845 | 0,088266 | 0,000000 | 0,000000 |
| 1 | 0 | 7.724.138.400 | 0,266464 | 0,000000 | 0,000000 |
| 2 | 0 | 9.512.133.400 | 0,328146 | 0,000000 | 0,000000 |
| 3 | 0 | 6.226.123.680 | 0,214786 | 0,000000 | 0,000000 |
| 4 | 3 | 2.362.591.575 | 0,081504 | 0,244511 | 0,733533 |
| 5 | 10 | 530.546.880 | 0,018303 | 0,183026 | 1,830259 |
| 6 | 56 | 68.605.200 | 0,002367 | 0,132536 | 7.422014 |
| 7 | 180 | 4.651.200 | 0,000160 | 0,028882 | 5.198747 |
| 8 | 1000 | 125.970 | 0,000004 | 0,004346 | 4,345661 |
| Total | 28.987.537.150 | 1.000000 | 0,593301 | 19.530214 |
Em seguida, vamos calcular o bônus médio. Podemos ver na tabela acima que o ganho médio, sem contar o bônus, é de 0,593301. No bônus, o jogador recebe 12 rodadas grátis dobradas. Assim, o ganho esperado do bônus é de 2 × 12 × 0,593301 = 14,239212.
Em seguida, vamos calcular a probabilidade de ganhar o bônus. Se o jogador acertar quatro números, a probabilidade de a 20ª bola ser um desses quatro é 4/20. Em geral, se o jogador acertar c números, a probabilidade de a 20ª bola ter contribuído para a vitória é c/20.
A fórmula para ganhar o bônus é prob(catch 4)*(4/20) + prob(catch 5)*(5/20) + prob(catch 6)*(6/20) + prob(catch 7)*(7/20) + prob(catch 8)*(8/20). Sabemos a probabilidade de qualquer vitória a partir da tabela de retornos acima. Portanto, a probabilidade de ganhar o bônus é:
0,081504*(4/20) + 0,018303*(5/20) + 0,002367*(6/20) + 0,000160*(7/20) + 0,000004*(8/20) = 0,021644.
Com a probabilidade de ganhar o bônus e o ganho médio do bônus, podemos calcular o retorno do bônus como 0,021644 × 14,239212 = 0,308198.
Não que precisemos saber, mas o retorno total do jogo é o retorno do jogo base mais o retorno do bônus, que é igual a 0,593301 + 0,308198 = 0,901498.
Agora, vamos começar a analisar a variância propriamente dita. Lembrando que uma fórmula geral para calcular a variância é:
var(x + y) = var(x) + var(y) + 2*cov(x,y), onde var representa a variância e cov representa a covariância. No caso deste jogo:
Variância total = var(jogo base) + var(bônus) + 2*cov(jogo base e bônus).
A fórmula fundamental para a variância é E(x^2) - [E(x)]^2. Em outras palavras, o quadrado esperado do ganho menos o quadrado do ganho esperado.
Dito isso, vamos começar com a variância do jogo base. Lembra quando eu disse antes que precisaríamos do quadrado da vitória esperada da primeira tabela? A célula inferior direita dessa primeira tabela nos mostra que o quadrado da vitória esperada é 19,530214. Já sabemos que a vitória esperada é 0,593301. Portanto, a variância do jogo base é 19,530214 - 0,593301² = 19,178208.
Em seguida, vamos calcular a variância do bônus (assumindo que ele já foi atingido). Para isso, lembre-se de que:
var(ax) = a 2 x, onde a é uma constante.
Lembre-se também que a variância de n variáveis aleatórias x é nx.
Dito isso, se x for o ganho base em um jogo bônus, então a variância de todo o bônus é 2² × 12 × x. Sabemos acima que a variância de uma única rodada no jogo base, sem contar o bônus, é igual a 19,178208. Portanto, a variância do bônus, dado que um bônus já foi atingido, é 2² × 12 × 19,178208 = 920,554000.
No entanto, o que precisamos saber é a variância do bônus antes do primeiro sorteio, incluindo a possibilidade de o bônus não ser ganho. Não, não podemos simplesmente multiplicar a variância do bônus pela probabilidade de ganhá-lo. Em vez disso, lembre-se de que var(x) = E(x^2) - [E(x)]^2. Vamos reorganizar isso para:
E(x^2) = var(x) + [E(x)]^2
Conhecemos a média e a variância do bônus, então o ganho esperado ao quadrado no bônus é 920,554000 + 19,178208 2 = 1123,309169.
Portanto, o quadrado esperado do ganho do bônus, antes do primeiro sorteio da bola, é prob(bônus) × E(x^2) = 0,021644 × 1123,309169 = 24,313239.
Já calculamos que o ganho esperado do bônus, antes da primeira bola, é de 0,308198. Portanto, a variância total do bônus, antes da primeira bola, é de 24,313239 - 0,308198 2 = 24,218253.
O próximo passo é calcular a covariância. "Por que existe uma correlação entre o ganho base e o ganho bônus?", você pode perguntar. Isso ocorre porque a última bola sorteada precisa contribuir para uma vitória para que o bônus seja ativado. Dado que a última bola contribuiu para uma vitória, o ganho médio aumenta. Lembrando que a fórmula de Bayes para probabilidade condicional diz:
P(A dado B) = P(A e B)/P(B).
Vamos então refazer nossa tabela de retorno para o jogo base, considerando que a última bola foi um acerto:
No Pick 8 Keno, a última bola foi acertada.
| Evento | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| 0 | 0 | - | 0,000000 | 0,000000 |
| 1 | 0 | - | 0,000000 | 0.000000 |
| 2 | 0 | - | 0,000000 | 0,000000 |
| 3 | 0 | - | 0,000000 | 0,000000 |
| 4 | 3 | 472.518.315 | 0,753119 | 2,259358 |
| 5 | 10 | 132.636.720 | 0,211402 | 2.114019 |
| 6 | 56 | 20.581.560 | 0,032804 | 1,837010 |
| 7 | 180 | 1.627.920 | 0,002595 | 0,467036 |
| 8 | 1000 | 50.388 | 0,000080 | 0,080310 |
| Total | 627.414.903 | 1.000000 | 6,757734 |
A célula inferior direita mostra que, supondo que a última bola tenha sido um acerto, a média de vitórias é de 6,757734.
Em seguida, lembre-se das suas aulas de estatística da faculdade:
cov(x,y) = exp(xy) - exp(x)*exp(y) .
No nosso caso, seja x = vitória no jogo base e y = vitória no bônus. Vamos trabalhar primeiro com exp(xy).
Exp(xy) = prob(bônus ganho)*(ganho médio no jogo base dado bônus ganho)*média(ganho com bônus) + prob(bônus não ganho)*(ganho médio no jogo base dado bônus não ganho)*média(ganho com bônus dado bônus não ganho). É fácil dizer que média(ganho com bônus dado bônus não ganho) = 0, então podemos reescrever como:
Exp(xy) = prob(ganho de bônus)*(ganho médio no jogo base dado ganho de bônus)*média(ganho de bônus) =
0,021644 × 6,757734 × 14,239212 = 2,082719.Já resolvemos para E(x) e E(y), então a covariância é:
cov(x,y) = exp(xy) - exp(x)*exp(y) = 2,082719 - 0,593301 × 0,308198 = 1,899865.
Vamos retornar à equação geral da variância quando a covariância está envolvida:
Variância total = var(jogo base) + var(bônus) + 2*cov(jogo base e bônus) = 19,178208 + 24,218253 + 2×1,899865 = 47,196191. O desvio padrão é a raiz quadrada disso, que é 6,869948.
Então, aqui está. Essa me levou horas, então espero que você esteja feliz.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Ouvi dizer que a probabilidade de um casamento terminar em divórcio, geralmente citada como 50% nos Estados Unidos, é calculada dividindo-se o número de divórcios pelo número de casamentos no mesmo período. Isso é verdade? Você acha que essa é uma maneira justa de calcular a estatística? Questiono isso porque se trata de comparar divórcios em um curto período com casamentos realizados ao longo de um longo período.
Se a população e a distribuição etária fossem estáveis, e se a probabilidade de divórcio fosse realmente de 50%, esperaríamos observar uma proporção de um divórcio para cada dois casamentos em qualquer período de tempo, considerando uma amostra de grande porte.
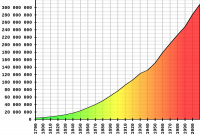
No entanto, a população não é estável. De acordo com este gráfico, parece que a população dos EUA está crescendo 10,71% por década. Isso equivale a 1,02% ao ano. Vamos arredondar para 1% para simplificar.
Fonte do mapa: Censo dos EUA
Segundo o site fatherly.com , a duração média de um casamento fracassado é de 8 anos.
Se você observasse uma proporção de 1 para 2 entre divórcios e casamentos atualmente, qual seria a probabilidade média de um casamento terminar em divórcio?
Os divórcios que vemos hoje são de casamentos ocorridos há 8 anos, quando a população era 92,35% da atual. Um cálculo simples sugere que a probabilidade real de divórcio é de 54,14%.
Vamos verificar isso.
Primeiro, de acordo com o CDC, há 6,9 casamentos para cada 1000 habitantes por ano. Esse dado não é relevante para a questão em pauta, mas acho que ajuda a visualizar os números envolvidos.
Suponha que a população há 8 anos era de 300.000.000. Isso representaria 0,69% * 300 milhões = 2.070.000 casamentos naquele ano.
Se 54,14% deles terminam em divórcio oito anos depois, então estaríamos vendo 2.070.000 * 54,14% = 1.120.698 divórcios atualmente.
1.120.698 / 2.070.000 = 50% da proporção observada de divórcios para casamentos na atualidade.
Para que ninguém diga nada, sim, eu sei que nem todos os divórcios terminam exatamente em oito anos. No entanto, considerando tudo, eu diria que o resultado final não ficará muito longe da minha taxa real de divórcio de 54,14%.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Seu escritório com 100 funcionários realiza uma troca de presentes de Amigo Secreto. A ideia é escrever o nome de cada pessoa em pedaços de papel individuais, colocá-los em um chapéu e todos sorteiam um nome aleatoriamente para dar um presente.
A questão é: quantos ciclos fechados haverá, em média? Por exemplo, em um ciclo fechado, Gordon doa para Don, que doa para Jon, que doa para Nathan, que doa para Gordon. Ou sorteando seu próprio nome.
Considere que cada pessoa está escolhendo uma opção por vez. À medida que cada pessoa escolhe, haverá dois tipos de situações:
- O nome de quem escolher já foi escolhido.
- O nome de quem escolheu ainda está na caixa de nomes.
Para qualquer pessoa que esteja selecionando, digamos que restem n pessoas para selecionar.
Se o nome de quem está escolhendo já tiver sido escolhido, há uma chance de 1/n de que a pessoa que está escolhendo feche um ciclo envolvendo seu nome. Por exemplo, digamos que Amy esteja escolhendo. O nome de Amy já pertence a Bob, o nome de Bob já pertence a Charlie e o nome de Charlie ainda está no recipiente. Com n nomes ainda no recipiente, há uma chance de 1/n de que Amy escolha o nome de Charlie, fechando um ciclo.
Se o nome de quem está escolhendo ainda não tiver sido escolhido, há uma chance de 1/n de Amy escolher o próprio nome, fechando o ciclo.
De qualquer forma, se a pessoa que recolhe os itens não fechar um ciclo, ela estará entrando em outra cadeia, que eventualmente será fechada por outra pessoa. Cada cadeia deve ser contada apenas uma vez, quando for fechada.
Assim, a resposta é 1/100 + 1/99 + 1/98 + ... + 1/1 = ~ 5,187377518.
Uma estimativa para qualquer número suficientemente grande de jogadores, n, é ln(n).
A questão é levantada e discutida no meu fórum, Wizard of Vegas .
Quanto valeria um wild extra garantido em uma máquina caça-níqueis de vídeo?
Isso depende de muitos fatores. A forma como interpretarei sua pergunta é: qual o valor de um símbolo Wild extra além da média que o jogador normalmente obtém? Embora a resposta varie bastante de jogo para jogo, um fator importante é o número de linhas na tela. Se houver três linhas, o Wild extra beneficiará 1/3 das linhas de pagamento. Da mesma forma, se houver quatro linhas, ele terá menos valor, afetando 1/4 das linhas de pagamento.
Para responder à sua pergunta, analisei o jogo Cleopatra , que já desmembrei. A tabela a seguir mostra o aumento no valor esperado de um símbolo Wild, em comparação com um número aleatório de símbolos Wild.
Valor do Extra Selvagem em Cleópatra
| Carretel | 3 linhas | 4 Linhas |
|---|---|---|
| 1 | 95,71% | 71,79% |
| 2 | 99,76% | 74,82% |
| 3 | 76,24% | 57,18% |
| 4 | 21,25% | 15,93% |
| 5 | 1,96% | 1,47% |