Pergunte ao Mago #318
Qual a melhor estratégia para jogar o Jogo da Corrida no programa "O Preço Certo", considerando que o jogador não tem ideia dos valores dos prêmios?
Para benefício dos leitores que não estão familiarizados com o jogo, aqui está um vídeo dele.
Acredito que a seguinte estratégia resulta em um número médio mínimo de turnos. Existem muitas estratégias que a igualariam, mas não creio que alguma consiga superá-la.
Para usar a estratégia, rotule as quatro etiquetas de preço como 1, 2, 3 e 4. Coloque-as nos quatro prêmios de acordo com o histórico de quantas você acertou no passado, começando pela primeira rodada à esquerda.
Estratégia de Jogo de Corrida
| História | Prêmio 1 | Prêmio 2 | Prêmio 3 | Prêmio 4 |
|---|---|---|---|---|
| Nenhum | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
A próxima tabela mostra a probabilidade de serem necessárias de 1 a 5 rodadas dentre as 24 maneiras possíveis de organizar as quatro etiquetas de preço.
Número de turnos necessários
| Viradas | Número | Probabilidade |
|---|---|---|
| 1 | 1 | 4,17% |
| 2 | 4 | 16,67% |
| 3 | 8 | 33,33% |
| 4 | 9 | 37,50% |
| 5 | 2 | 8,33% |
| Total | 24 | 100,00% |
Calculando o produto escalar, o número médio de turnos necessários, segundo essa estratégia, é de 3,29167.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
No episódio de 18 de setembro de 2019 do Jeopardy!, havia uma categoria intitulada "Descreva o Jogo de Cassino". Uma das dicas era: "Vestido elegantemente e jogando com muita classe; Horário comercial; O que o traz a Mônaco, Sr. Bond?"

A resposta fornecida foi "bacará", que foi considerada correta. Bond não estava jogando chemin de fer?
Sim, de fato Bond estava jogando Chemin de fer , não bacará . Só para relembrar, as principais diferenças são:
- A vez de bancar gira em torno da mesa. O jogador que banca assume automaticamente a mão do Banqueiro*.
- Tanto o Jogador* quanto o Banqueiro têm livre arbítrio para comprar uma terceira carta, desde que nenhum deles tenha um 8 ou 9 natural de duas cartas.
Observação:
Como de costume, ao escrever sobre bacará ou chemin de fer, uso maiúsculas nos nomes das apostas para evitar confusão com os jogadores.
Dito isso, a primeira cena desse tipo está no clipe de Dr. No abaixo, onde não apenas o banco gira, os jogadores têm livre arbítrio na terceira carta, mas Bond chega a se referir ao jogo verbalmente como "chemin de fer" no minuto 2:11 do vídeo:
O próximo vídeo mostra três cenas de "chemin de fer" de três filmes diferentes.
Aqui estão os pontos de partida de cada cena:
- 2:09 — Thunderball
- 4:19 — A Serviço Secreto de Sua Majestade
- 7:30 — Somente Para Seus Olhos
Nos três jogos, vemos os jogadores utilizando o sistema bancário e o livre arbítrio na decisão da terceira carta, especialmente em "For Your Eyes Only", onde as probabilidades são discutidas.
Por fim, abaixo está a cena de Goldeneye.
Aqui vemos novamente a alternância entre a aposta e o banco, com a possibilidade de livre arbítrio na compra de uma terceira carta. No entanto, a personagem feminina se refere ao jogo como "bacará" aos 0:45. Eu classificaria isso como um "erro de personagem".
Em suma, não há dúvidas de que Bond jogava chemin de fer em todos os filmes. Tecnicamente, acho que os juízes erraram ao aceitar "bacará" como resposta correta. No entanto, não os culpo. Mesmo para os padrões do Jeopardy, esperar que o jogador médio saiba a diferença entre bacará e chemin de fer seria demais. O fato de terem aceitado a resposta "The Mooch" em vez de Anthony Scaramucci demonstra que eles estão ficando mais tolerantes.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Como perguntado no filme Meninas Malvadas , o que é:
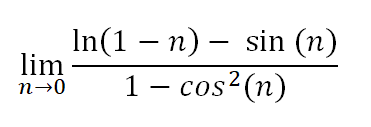
Vamos começar observando um gráfico de n (eixo x) por f(n) (eixo y).
Como você pode ver, o limite tende a ∞ pela esquerda e a -∞ pela direita. Como a reta não converge para o mesmo lugar por ambos os lados, não há limite.
No entanto, vamos responder à pergunta sem usar um gráfico. A regra de L'Hôpital diz que se o limite de f(x)/g(x) = 0/0, então lim f(x)/g(x) = lim f'(x)/g'(x). Portanto, vamos resolver para f'(x) e g'(x).
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos² (n)) d/dn = sin² (n) d/dn
Vamos usar a regra do produto para resolver sin² (n) d/dn
pecado 2 (n) d/dn = pecado (n) × pecado (n) d/dn =
sen(n) × cos(n) + cos(n) × sen(n) =
2sen(n)cos(n).
Em seguida, vamos resolver para f'(n) e g'(n) em n = 0.
f'(0) = -1/(1-0) - cos(0) = -2.
g'(0) = 2sen(0)cos(0) = 0
Portanto, f'(0)/g'(0) = -2/0 = -∞. Assim, o limite da função original não existe.

Gostaria de parabenizar os roteiristas de Meninas Malvadas por terem acertado em cheio na matemática do filme. Até mesmo filmes que abordam matemática de forma séria, como Gênio Indomável, muitas vezes erram feio nos cálculos.