Pergunte ao Mago #322
Sentei-me para jogar Texas Hold'em e a melhor mão da rodada era um straight flush. Dois outros jogadores na mesa comentaram que era o terceiro straight flush consecutivo. Qual a probabilidade disso?
Em um jogo de Texas Hold 'Em com 10 jogadores, assumindo que ninguém desista, a probabilidade de a mão mais alta ser uma sequência ou um royal flush é de 1 em 350,14. A probabilidade de isso acontecer em três mãos, em três tentativas, é de 1 em 42.926.491.
No entanto, aquela mesa pode ter durado horas. Talvez uma pergunta mais realista seja qual a probabilidade de isso acontecer pelo menos uma vez em um dia inteiro. Supondo 24 horas de jogo e 24 mãos por hora, a resposta para essa pergunta seria 1 em 59.621.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Considerando uma estratégia adequada, qual é a probabilidade de ganhar com um aumento de 4x no Ultimate Texas Hold 'Em? Registrei 96 mãos com aumento de 4x. Sem contar os empates, tive 66 vitórias e 30 derrotas. Como isso se compara às expectativas?
Considerando uma estratégia correta de aumento de 4x, a probabilidade de cada resultado, dado um aumento de 4x, é a seguinte:
- Vitória: 58,82%
- Perda: 38,47%
- Empate: 2,72%
Se excluirmos os empates, a probabilidade de vitória é de 60,46%. Em 96 mãos resolvidas, o número esperado de vitórias com quatro mãos vencedoras é de 58,04. Portanto, 66 vitórias superam as expectativas, mas não de forma significativa.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Axel e Bob têm cada um seu próprio baralho de 52 cartas. Ambos embaralham os baralhos aleatoriamente. Em seguida, viram uma carta de cada vez, simultaneamente, de cada baralho. Qual é a probabilidade de que eles virem a mesma carta ao mesmo tempo pelo menos uma vez?
Seria fácil estimar a resposta como 1-(51/52) 52 = 0,63568648. No entanto, estimativas são intelectualmente insatisfatórias. Então, vamos encontrar uma solução exata!
Passo 1: Para começar, considere o número de maneiras pelas quais o segundo baralho pode ser ordenado onde a primeira carta é o número 1. A resposta é o número de maneiras de ordenar as outras 51 cartas, que é 51! = 1551118753287382280224243016469303211063259720016986112000000000000.
Qualquer carta pode combinar com o primeiro baralho, então devemos fazer isso para todas as 52 cartas. Isso nos dá 52 * 51! = 52! combinações onde pelo menos uma carta combina.
Passo 2: No entanto, o passo 1 conta duas vezes cada situação em que duas cartas combinam. Por exemplo, se as duas primeiras cartas fossem 1 e 2, teríamos contado as 50! maneiras de organizar as outras cartas duas vezes, uma vez com 1 como a primeira carta e uma segunda vez com 2 como a segunda carta. O número de maneiras de escolher 2 cartas dentre 52 é combin(52,2) = 1326. Para cada combinação de duas cartas, existem 50! = 30414093201713378043612608166064768844377641568960512000000000000 maneiras de ordenar as outras cartas. Assim, para o passo 2, precisamos subtrair combin(52,2)*50! = (52*51/2!)*50! = 52!/2! combinações.
Passo 3: Em seguida, considere a situação em que as três primeiras cartas do baralho aleatório são 1, 2 e 3, nessa ordem. Existem 49! maneiras de ordenar as outras 49 cartas. Teríamos contado essas combinações três vezes na etapa inicial de contagem de pelo menos uma carta correspondente. Depois, teríamos subtraído todas as combinações (3,2) = 3 maneiras de escolher 2 dessas três cartas na segunda etapa. Portanto, essa situação teria sido contada 3 - 3 = 0 vezes, então precisamos adicioná-las novamente. Existem combinações (52,3) de situações em que se escolhe pelo menos 3 cartas correspondentes. Assim, precisamos adicionar de volta combinações (52,3) * 49! = 52 * 51 * 50 * 49! / 3! = 52! / 3! combinações.
Passo 4: Em seguida, considere a situação em que as quatro primeiras cartas do baralho aleatório são 1, 2, 3 e 4, nessa ordem. Existem 48! maneiras de ordenar as outras 48 cartas. Teríamos contado cada uma delas quatro vezes na etapa inicial de contagem, buscando pelo menos uma carta correspondente. Depois, teríamos subtraído todas as combinações (4,2) = 6 maneiras de escolher duas dessas quatro cartas na etapa 2. Em seguida, teríamos adicionado todas as combinações (4,3) = 4 maneiras de escolher 3 dessas quatro cartas. Portanto, temos 4 - 6 + 4 = 2 maneiras de cada situação ser contada. Assim, precisamos subtrair uma dessas maneiras, para que cada situação seja contada apenas uma vez. Existem combinações (52,4) * 48! = 52 * 51 * 50 * 49 * 48! / 4! = 52! / 4! situações que precisam ser adicionadas novamente.
Continuaremos fazendo isso, alternando adições e subtrações para corrigir a contagem dupla.
No final, o número de situações em que pelo menos uma carta no baralho aleatório corresponde ao baralho ordenado = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
Existem 52! = y = 527177615496365219422618541545122659969212453861982208000000000000 maneiras totais de ordenar 52 cartas.
Portanto, a resposta é x/y = 0,6321205588285576784044762298
A probabilidade de não haver correspondências é 1-(x/y) = 0,3678794411714423215955237702.
Se esse número lhe parece familiar, é porque deveria. 1/e = 0,3678794411714423215955237702.
Portanto, a resposta pode ser estimada com bastante precisão como 1-(1/e).
Agradecimentos
Os cálculos matemáticos foram realizados em Pari/GP
Este problema foi levantado e discutido no meu fórum no Wizard of Vegas .
No documento intitulado "Probabilidades de padrões de bingo (PDF)" em seu site, você indica que o número esperado de chamadas para encontrar um vencedor, assumindo 300 cartelas em jogo, é o seguinte:
- Quatro cantos: 8,43
- Diamante pequeno: 11,833
Ambos os padrões exigem apenas quatro marcas e têm apenas uma maneira de ganhar. Por que o número esperado de bolas para encontrar um vencedor é diferente?
Essa é uma resposta difícil de explicar. Para começar, o número esperado de chamadas em um jogo com uma única carta seria o mesmo. No entanto, há um efeito de correlação quando se joga com mais de uma carta.
É difícil dar uma resposta rápida para essa pergunta, mas, se fosse necessário, diria que é porque o padrão de quatro cantos exige uma concentração de bolas nas colunas B e O. Já o padrão de diamante pequeno tem maior probabilidade de ser atingido com uma distribuição mais uniforme de bolas pelas colunas B, N e O.
Vamos simplificar o jogo para um em que haja um número infinito de cartas em jogo e as bolas sejam retiradas COM reposição. Aqui está o número de bolas necessárias para obter um vencedor em ambos os jogos:
- Quatro cantos: 2,5 + 2,5 + ((1/2) * 10 + (1/2) * (2,5 + 5)) = 13,75
- Diamante pequeno: =(5/3)+((1/3)*((5/3)+(5/2)+5)+(2/3)*((5/2)+((1/2)*((5/2)+5)+(1/2)*(5+5)))) = 12 + 2/9
Isso mostra que os quatro cantos exigem 1,53 bolas a mais.
Executando isso em uma simulação sob as regras normais do bingo, assumindo cartelas infinitas, aqui estão os resultados:
- Quatro cantos: 12,8289
- Diamante: 11,3645
Desta vez, uma diferença de 1,46 bolas.
O que espero ter demonstrado é que os padrões têm maior probabilidade de serem descobertos mais rapidamente se as marcas forem distribuídas por mais colunas. Por esse motivo, acredito que em um jogo de bingo simples, geralmente se observa que a combinação vencedora é horizontal.
Essa pergunta foi feita e discutida no meu fórum, Wizard of Vegas .
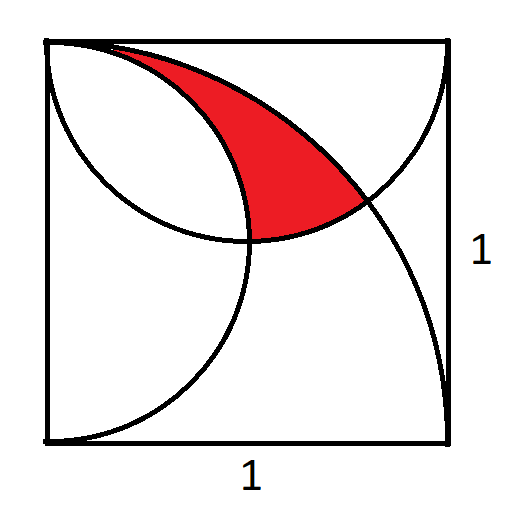
Na figura acima, há um quarto de círculo e dois semicírculos inscritos em um quadrado de lado unitário. A pergunta é: qual é a área da região vermelha?
Clique no botão a seguir para ver minha resposta.
Clique no botão a seguir para ver minha solução.
Aqui está um link para a minha solução . (PDF)
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Agradecimentos: Gostaria de agradecer ao Mind Your Decisions por este quebra-cabeça matemático.


