Pergunte ao Mago #323
Essa aposta combinada é boa?

Na primeira etapa, você precisa apostar em qualquer resultado contra o spread em um jogo da NFL. No momento em que você fez esta pergunta (2 de janeiro de 2020), os Vikings eram azarões por 7,5 pontos. De acordo com minha calculadora de spread alternativo da NFL , a probabilidade de os Vikings +8,5 vencerem é de 52,22%.
Para todos os outros jogos, analisei as odds atuais, subtraí a taxa de serviço e obtive a probabilidade de vitória. Dito isso, a tabela a seguir mostra a probabilidade de cada aposta ser vencedora.
Cartão Parlay da William Hill
| Perna | Vinho Justo | Prob. Vitória |
|---|---|---|
| Santos -8,5 | -7,5 | 47,78% |
| Vikings +8,5 | 8,5 | 52,22% |
| Hou | -135 | 57,45% |
| Contas | 135 | 42,55% |
| Patriotas | -205 | 67,21% |
| Titãs | 205 | 32,79% |
| Mar | -118 | 54,13% |
| Phil | 118 | 45,87% |
| LSU | -200 | 66,67% |
| Clemson | 200 | 33,33% |
| AFC | -130 | 56,52% |
| NFC | 130 | 43,48% |
As duas equipes com maior probabilidade de vitória na primeira etapa são os Patriots e o LSU. Aqui está a probabilidade de minhas recomendações de vitória:
- Vikings +8,5 — 52,22%
- Patriotas — 67,21%
- LSU — 66,67%
O produto dessas probabilidades é 23,40%. Acertar 4 para 1 resulta em um retorno de 4 × 23,40% = 93,60%. Em outras palavras, a vantagem da casa é de 6,40%. Portanto, eu deixaria essa de lado.
Estou pensando em criar uma aposta paralela para variantes de blackjack "push 22" que pagaria 11 para 1 se o dealer estourasse com 22. Quais seriam as probabilidades?
Estou pensando em criar uma aposta paralela para variantes de blackjack "push 22" que ganharia se o dealer ultrapassasse 22. Quais seriam as probabilidades de pagamento e qual seria a vantagem da casa?
Supondo que o dealer sempre compre todas as cartas da sua mão (mesmo que todos os jogadores já tenham estourado), então mostro uma probabilidade de estourar com 22 de 7,88% se o dealer parar no 17 suave e de 8,00% se ele pedir carta com um 17 suave.
Supondo que o dealer tire um 17 suave, com uma aposta de 11 para 1, a vantagem da casa seria de 4,04%. Com uma aposta de 10 para 1, essa vantagem sobe para 12,04%.
Devo avisá-los e orientar os jogadores de que isso seria contabilizado (cala a boca, Wiz!).
Amy e Bob estão competindo para ver quem ganha primeiro em quatro lançamentos de uma moeda honesta. Amy quer apostar US$ 8.000 em si mesma para ganhar a competição. No entanto, ela só pode apostar em um lançamento por vez. Todas as apostas pagam o mesmo valor apostado. Como ela pode estruturar suas apostas para ganhar US$ 8.000 se vencer a série completa e perder US$ 8.000 se Bob vencer?
Clique no botão abaixo para ver a resposta.
Existem 16 possíveis situações intermediárias. A tabela a seguir mostra a aposta que Amy deve fazer em cada uma delas e seu saldo antes da aposta, seguindo essa estratégia.
Responder
| Amy | Prumo | Equilíbrio | Aposta |
|---|---|---|---|
| 0 | 0 | 0 | 2500 |
| 0 | 1 | -2500 | 2500 |
| 0 | 2 | -5000 | 2000 |
| 0 | 3 | -7000 | 1000 |
| 1 | 0 | 2500 | 2500 |
| 1 | 1 | 0 | 3000 |
| 1 | 2 | -3000 | 3000 |
| 1 | 3 | -6000 | 2000 |
| 2 | 0 | 5000 | 2000 |
| 2 | 1 | 3000 | 3000 |
| 2 | 2 | 0 | 4000 |
| 2 | 3 | -4000 | 4000 |
| 3 | 0 | 7000 | 1000 |
| 3 | 1 | 6000 | 2000 |
| 3 | 2 | 4000 | 4000 |
| 3 | 3 | 0 | 8000 |
Clique no botão abaixo para ver a solução.
Deixar:
- a = Amy vence
- b = Bob vence
- w = saldo de vitórias de Amy até o momento na série
- f(a,b,w) = Valor da aposta de Amy no próximo jogo
Em quebra-cabeças como este, geralmente é uma boa estratégia começar pelo fim e ir resolvendo em direção ao início. Dito isso, é fácil perceber que:
f(3,3,0) = 8.000
Nessa situação, o sétimo jogo é "tudo ou nada". Amy deve ter ganhos de 0 e apostar 8.000 no último lançamento de moeda, o que lhe dará um ganho de 8.000 se ela ganhar o lançamento e uma perda de 8.000 caso contrário.
Voltando um passo atrás, e se ela tiver 3 vitórias e Bob tiver 2? Se ela ganhar a próxima jogada, ela ganha o jogo todo. Se ela perder, ficará com um placar de 3-3. De acordo com f(3,3,0), ela deveria ter 0 se o placar for 3-3. Portanto, precisamos que ela tenha 8.000 se ganhar a próxima jogada e 0 caso contrário. O que obteremos aqui é um lucro líquido de 4.000 e uma aposta do mesmo valor. Então:
f(3,2,4000)=4000
Recuando um pouco, e se ela tiver 3 vitórias e Bob tiver 1? Se ela ganhar o próximo lançamento, ela ganha o jogo todo. Se ela perder, ficará com um placar de 3 a 2. De acordo com f(3,2,4000), ela deveria ter 4.000 se o placar for 3 a 2. Portanto, precisamos que ela tenha 8.000 se ganhar o próximo lançamento e 4.000 caso contrário. O que obteremos aqui é um lucro líquido no meio [(4.000 + 8.000) / 2 = 6.000] e uma aposta na metade da distância entre esses dois objetivos, [(8.000 - 4.000) / 2 = 2.000]. Então:
f(3,1,6000) = 2.000
Recuando um pouco, e se ela tiver 3 vitórias e Bob não tiver nenhuma? Se ela ganhar o próximo lançamento, ela ganha o jogo todo. Se ela perder, ficará com um placar de 3 a 1. De acordo com f(3,1,6000), ela deveria ter 6.000 se o placar for 3 a 1. Portanto, precisamos que ela tenha 8.000 se ganhar o próximo lançamento e 6.000 caso contrário. O que obteremos aqui é um lucro líquido no meio [(6.000 + 8.000) / 2 = 7.000] e uma aposta na metade da distância entre esses dois objetivos, [(8.000 - 4.000) / 2 = 2.000]. Então:
f(3,0,7000) = 1.000
É importante ressaltar que Amy deve ter um saldo positivo de 0 se o placar estiver empatado. Em qualquer cenário de empate, sua probabilidade de vencer a série inteira será de 50%. Com metas equilibradas de 8.000 pontos em cada caso, ela precisa apostar em 0 ou corre o risco de não atingir nenhuma das metas finais.
Em seguida, se Amy estiver em desvantagem na série, seu ganho líquido deve ser -1 vezes o ganho líquido que ela teria se estivesse em vantagem pela mesma pontuação. Por exemplo, considere uma pontuação de Amy 2 - Bob 3 (ou 2-3). Se ela perder a próxima jogada, perde o jogo inteiro. Se ela ganhar, ficará com uma pontuação de 3-3. De acordo com f(3,3,0), ela deve ter 0 se a pontuação for 3-3. Portanto, precisamos que ela tenha 0 se ganhar a próxima jogada e -8000 caso contrário. O que teremos aqui é uma perda líquida de 4000 e uma aposta do mesmo valor. Então:
f(2,3,-4000)=4000
Seguindo a mesma lógica:
f(1,3,-6000) = 2000
f(0,3,-7000) = 1.000
Em seguida, qual deve ser a aposta de Amy se o placar estiver 2-2? Se ela ganhar o cara ou coroa, o placar será 3-2. Como vimos acima, ela precisa ter um lucro líquido de 4.000 com esse placar. Também vemos que, se ela estiver perdendo por 2-3, precisa ter uma perda líquida de 4.000. Portanto, ela precisa apostar 4.000.
f(2,2,0) = 4.000
Recuando um passo, e se o placar for 2 a 1? Estabelecemos que ela precisa ter um lucro líquido de 6.000 se ganhar a próxima jogada (placar de 3 a 1) e um lucro líquido de 0 se perder (placar de 2 a 2). O que ela conseguirá aqui é um lucro líquido intermediário [(6.000 + 0) / 2 = 3.000] e uma aposta equivalente à metade da diferença entre esses dois objetivos, [(6.000 - 0) / 2 = 3.000]. Portanto:
f(2,1,3000) = 3000
Recuando um pouco mais, e se ela tiver 2 vitórias e Bob não tiver nenhuma? Se ela ganhar a próxima rodada, o placar será 3 a 0. Se ela perder, será 2 a 1. Ela deverá ter um lucro líquido de 7.000 com 3 a 0 e 3.000 com 2 a 1. O que ela receberá a partir de um placar de 2 a 0 é um lucro líquido intermediário [(7.000 + 3.000) / 2 = 5.000] e uma aposta na metade da diferença entre esses dois objetivos, [(7.000 - 3.000) / 2 = 2.000]. Portanto:
f(2,0,5000) = 2000
Ao inverter as pontuações, de forma que Alice tenha duas vitórias e Bob tenha menos, também sabemos:
f(1,2,-3000) = 3000
f(0,2,-5000) = 2000
Como explicado anteriormente, o lucro líquido de Amy deve ser 0 se a série estiver equilibrada, portanto, com um placar de 1 a 1, seu lucro líquido deve ser 0. Com um placar de 2 a 1, ela precisa ter um lucro de 2.000 e com um placar de 1 a 2, ela precisa ter um prejuízo de 2.000. Assim, com um empate de 1 a 1, ela deve apostar 2.000, ou seja:
f(1,1,0) = 2.000
E se Amy estiver ganhando por 1 a 0? Já estabelecemos que ela precisa estar com 5.000 pontos de vantagem quando o placar está 2 a 0. Quando está 1 a 1, ela precisa estar empatada.O que se obterá aqui, partindo de um placar de 1 a 0, é um lucro líquido no meio [(5.000 + 0) / 2 = 2.500] e uma aposta na metade da distância entre esses dois gols, [(5.000 - 0) / 2 = 2.500]. Portanto:
f(1,0,2500) = 2.500
Ao inverter o placar para 0-1:
f(0,1,-2500) = 2.500
Então, finalmente, chegamos ao primeiro jogo com o placar de 0 a 0. Precisamos que Amy esteja com um lucro de 2.500 se ganhar a próxima rodada e com um prejuízo de 2.500 se perder. Portanto, uma aposta de 2.500 nos levará a esse objetivo. Ou:
f(0,0,0) = 2.500
Essa questão é levantada e discutida no meu fórum no Wizard of Vegas .
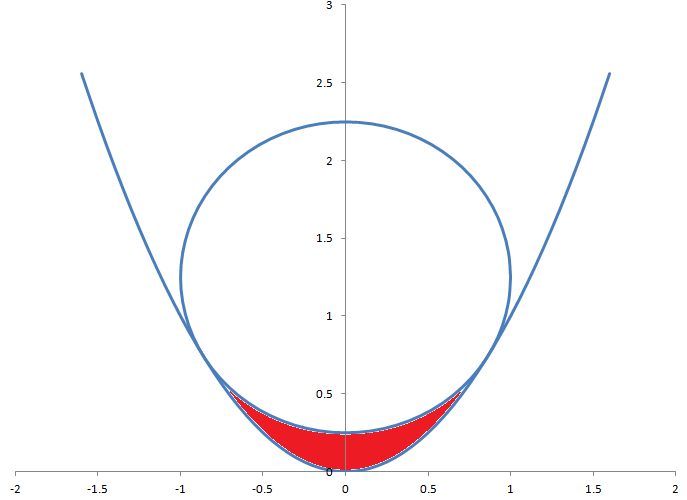
Um círculo de raio 1 é tangente a uma parábola de equação y = x² . Qual é a área da região em vermelho entre o círculo e a parábola?
Clique no botão abaixo para ver a resposta.
Aqui está minha solução . (PDF)
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Recebi essa informação de Presh Talwalker, da Mind Your Decisions .


