WOO logo

Recomendações do Mago

Pergunte ao Mago #326

O que é a estratégia Cruz de Ferro no craps e o que você acha dela?

anônimo

A Cruz de Ferro é uma forma de apostar no campo e em apostas de lugar para ganhar em qualquer lançamento de dados, exceto no 7. O campo já cobre os números 2, 3, 4, 9, 10, 11 e 12. O jogador adicionará a isso apostas de lugar nos números 5, 6 e 8 para cobrir os números restantes, exceto o 7. A tabela a seguir mostra como fica o cálculo com uma aposta de campo de $5, uma aposta de lugar de $5 no 5 e apostas de lugar de $6 no 6 e no 8.

Cruz de Ferro

Total de dados Ganhar Combinações Probabilidade Retornar
2 10 1 0,027778 0,277778
3 5 2 0,055556 0,277778
4 5 3 0,083333 0,416667
5 2 4 0,111111 0,222222
6 2 5 0,138889 0,277778
7 -22 6 0,166667 -3,666667
8 2 5 0,138889 0,277778
9 5 4 0,111111 0,555556
10 5 3 0,083333 0,416667
11 5 2 0,055556 0,277778
12 15 1 0,027778 0,416667
36 1.000000 -0,250000

A célula inferior direita da tabela mostra uma perda esperada de $0,25. O valor total apostado é de $22. Isso faz com que a vantagem total da casa seja de $0,25/$22 = 1/88 = 1,14%.

Neste ponto, você pode estar se perguntando como essa vantagem da casa pode ser menor do que a vantagem da casa de cada aposta individual. A resposta é que a vantagem da casa de 1,52% ao apostar no 6 e no 8 e de 4,00% ao apostar no 5 é baseada em cada aposta resolvida. Se definirmos a vantagem da casa nas apostas de lugar por rodada, então a vantagem da casa ao apostar no 6 ou no 8 é de 0,46% e no 5 é de 1,11%.

Podemos chegar à vantagem da casa de 1,14% calculando a média ponderada de todas as apostas feitas, da seguinte forma:

($5*2,78% + $5*1,11% + $12*0,46%)/22 = $0,25/$22 = 1,14%.

Desconfie de cassinos que pagam apenas 2 para 1 no número 12 da aposta no campo. Insista em receber o pagamento integral de 3 para 1. O pagamento menor dobra a vantagem da casa nessa aposta, de 2,78% para 5,56%.

Na minha opinião, comparado à maioria dos jogos, 1,14% é uma aposta bastante razoável. No entanto, você pode se sair muito melhor no craps. Por exemplo, com odds de 3, 4 ou 5x, fazendo as apostas Pass e Come com odds completas, você pode reduzir a vantagem da casa para 0,37%. Fazendo o oposto, apostando em Don't Pass e Don't Come, além de apostar com odds completas, a vantagem da casa cai para 0,27%.

Qual é o número esperado de lançamentos de um dado honesto para que cada face apareça pelo menos duas vezes?

Ace2

A resposta é 390968681 / 16200000 = aproximadamente 24,13386919753086

Embora isso pudesse ser resolvido com uma longa e tediosa cadeia de Markov, eu prefiro uma solução integral. Explico como usar esse método nas minhas páginas sobre Fire Bet e Bonus Craps .

Imagine que, em vez de os eventos significativos serem determinados pelo lançamento de um dado, um de cada vez, considere-os como um instante no tempo. Suponha que o intervalo de tempo entre os eventos tenha uma propriedade de ausência de memória, com um tempo médio entre eventos de uma unidade de tempo. Em outras palavras, o intervalo de tempo entre os eventos segue uma distribuição exponencial com média de 1. Isso não será relevante para fins de resolução da aposta, pois os eventos ainda ocorrerão um de cada vez.

De acordo com a distribuição de Poisson, a probabilidade de que qualquer face do dado tenha sido lançada zero vezes em x unidades de tempo é exp(-x/6)*(x/6) = 0 / 0! = exp(-x/6). A distribuição de Poisson também afirma que a probabilidade de que qualquer face seja lançada exatamente uma vez é exp(-x/6)*(x/6) = 1 / 1! = exp(-x/6) * (x/6). Assim, a probabilidade de que qualquer face tenha sido lançada duas ou mais vezes em x unidades de tempo é 1 - exp(-x/6)*(1 + (x/6)). A probabilidade de que todas as seis faces tenham sido lançadas pelo menos duas vezes é (1 - exp(-x/6)*(1 + (x/6))) = 6. A probabilidade de que pelo menos uma face não tenha sido lançada pelo menos duas vezes é igual a:

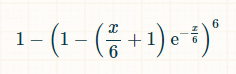
Dobre cada lado duas vezes

Precisamos integrar isso ao longo de todo o período para descobrir quanto tempo, em média, transcorrerá sem que o objetivo desejado seja alcançado.

Felizmente, podemos usar uma calculadora de integrais neste ponto. Para a calculadora indicada, insira 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = aproximadamente 24,1338692 na caixa de texto após "Calcular a integral de" e, em personalizado, defina o limite de integração de 0 a ∞.

A resposta é 390968681 / 16200000 = aproximadamente 24,13386919753086

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .

Tenho uma pergunta em duas partes.

Para a parte 1, dado:
  • x + y + z = 1
  • x² + y² + z² = 4
  • x^3 + y^3 + z^3 = 9

Qual é o resultado de x^4 + y^4 + z^4?

Na segunda parte, qual é a resposta para o caso geral quando:

  • x + y + z = a
  • x² + y² + z² = b
  • x^3 + y^3 + z^3 = c

anônimo

Pergunta 1: 97/6 = aproximadamente 16,166666

Questão 2: a⁴ /6 + (4/3)ac - a²b + b² /2

Para ver minha solução (PDF)

Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .

Você começa com um dado honesto de 6 lados e o lança seis vezes, registrando os resultados de cada lançamento. Em seguida, você escreve esses números nas seis faces de outro dado honesto, sem rótulos. Por exemplo, se seus seis lançamentos foram 3, 5, 3, 6, 1 e 2, então seu segundo dado não teria um 4; em vez disso, teria dois 3s.

Em seguida, você lança este segundo dado seis vezes. Você pega esses seis números e os escreve nas faces de um terceiro dado honesto, e continua esse processo de gerar um novo dado a partir do anterior.

Eventualmente, você terá um dado com o mesmo número em todas as seis faces. Qual é o número médio de transições de um dado para outro (ou o total de lançamentos dividido por 6) para chegar a esse estado?

rsactuary

Aprox. 9,65599148388557

Para evitar confusão, vamos rotular o dado inicial com letras em vez de números. Vamos rotular cada estado possível do dado com letras. Por exemplo, AAABBC significaria três de uma letra, duas de outra e uma de uma terceira. O estado inicial seria obviamente ABCDEF.

Seja E(ABCDEF) o número esperado de lançamentos a partir do estado ABCDEF.

E (ABCDEF) = 1 + [180 × E (AAAAAB) + 450 × E (AAAABB) + 300 × E (AAABBB) + 1800 × E (AAAABC) + 7200 × E (AAABBC) + 1800 × E (AABBCC) + 7200 × E (AAABCD) + 16200 × E (AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656

Com base no número de combinações de transição entre estados, a seguinte matriz de transição mostra quantas maneiras existem de ir de cada estado inicial (coluna da esquerda) para cada novo estado. Aliás, levou algumas horas para construí-la corretamente.

Matriz de Transição A

Estado
Antes		 AAAAAA AAAAAB AAAABB AAABBB AAAABC AAABBC AABBCC AAABCD AABBCD AABCDE ABCDEF
AAAAAB 15.626 18.780 9.750 2.500 - - - - - - -
AAAABB 4.160 13.056 19.200 10.240 - - - - - - -
AAABBB 1.458 8.748 21.870 14.580 - - - - - - -
AAAABC 4.098 12.348 8.190 2.580 7.920 10.080 1.440 - - - -
AAABBC 794 5.172 8.670 5.020 6.480 17.280 3.240 - - - -
AABBCC 192 2.304 5.760 3.840 5.760 23.040 5.760 - - - -
AAABCD 732 4.464 4.140 1.680 7.920 14.400 2.520 4.320 6.480 - -
AABBCD 130 1.596 3.150 1.940 5.280 16.800 3.600 4.800 9.360 - -
AABCDE 68 888 1.380 760 3.960 11.520 2.520 7.200 14.040 4.320 -
ABCDEF 6 180 450 300 1.800 7.200 1.800 7.200 16.200 10.800 720

Não vou me alongar em álgebra matricial, exceto para dizer que, digamos, a matriz B seja a seguinte:

Matriz B

Estado
Antes		 AAAAAB AAAABB AAABBB AAAABC AAABBC AABBCC AAABCD AABBCD AABCDE ABCDEF
AAAAAB -27876 9750 2500 0 0 0 0 0 0 -46656
AAAABB 13056 -27456 10240 0 0 0 0 0 0 -46656
AAABBB 8748 21870 -32076 0 0 0 0 0 0 -46656
AAAABC 12348 8190 2580 -38736 10080 1440 0 0 0 -46656
AAABBC 5172 8670 5020 6480 -29376 3240 0 0 0 -46656
AABBCC 2304 5760 3840 5760 23040 -40896 0 0 0 -46656
AAABCD 4464 4140 1680 7920 14400 2520 -42336 6480 0 -46656
AABBCD 1596 3150 1940 5280 16800 3600 4800 -37296 0 -46656
AABCDE 888 1380 760 3960 11520 2520 7200 14040 -42336 -46656
ABCDEF 180 450 300 1800 7200 1800 7200 16200 10800 -46656

A resposta é o determinante da matriz B em relação ao determinante da matriz A:

Determ(A) = 1.461.067.501.120.670.000.000.000.000.000.000.000.000.000.000

Determ(B) = 14.108.055.348.203.100.000.000.000.000.000.000.000.000.000.000

Determ(B) / Determ(A) = aproximadamente 9,65599148388557