WOO logo

Recomendações do Mago

Pergunte ao Mago #335

Li sobre o jogo Reversible Royal com retorno de 105,22% no seu artigo no Wizard of Vegas. Esse retorno pressupõe uma estratégia ótima, incluindo a ordem das cartas. Qual seria o retorno se eu considerasse uma vitória média em um Royal Flush? E se eu usasse a estratégia comum do Bonus Poker 6-5, que é a tabela de pagamento básica?

anônimo

Considerando que não haja desvios de estratégia, 1 em cada 60 Royals será sequencial. O jackpot do Royal reversível paga 161.556 por 1. Qualquer outro Royal paga 800 por 1. O ganho médio do Royal é, portanto, (1/60)*161.556 + (59/60)*800 + 17.396 por 1.

Se assumirmos que todos os Royals pagam 17.396 e jogarmos a estratégia ideal com base nessa vitória do Royal, o retorno cai para 103,56%.

Se jogarmos com a estratégia padrão de Bonus Poker 6-5, que é a tabela de pagamento base, o retorno cai ainda mais para 101,97%.

Considere o quadrado unitário com coordenadas (0,0), (1,0), (1,1), (0,1). A reta A vai de (0,0) a (1,1). A reta B vai de (1,0) a (0,5,1). Qual é o raio da circunferência tangente às retas A, B e à base da circunferência?

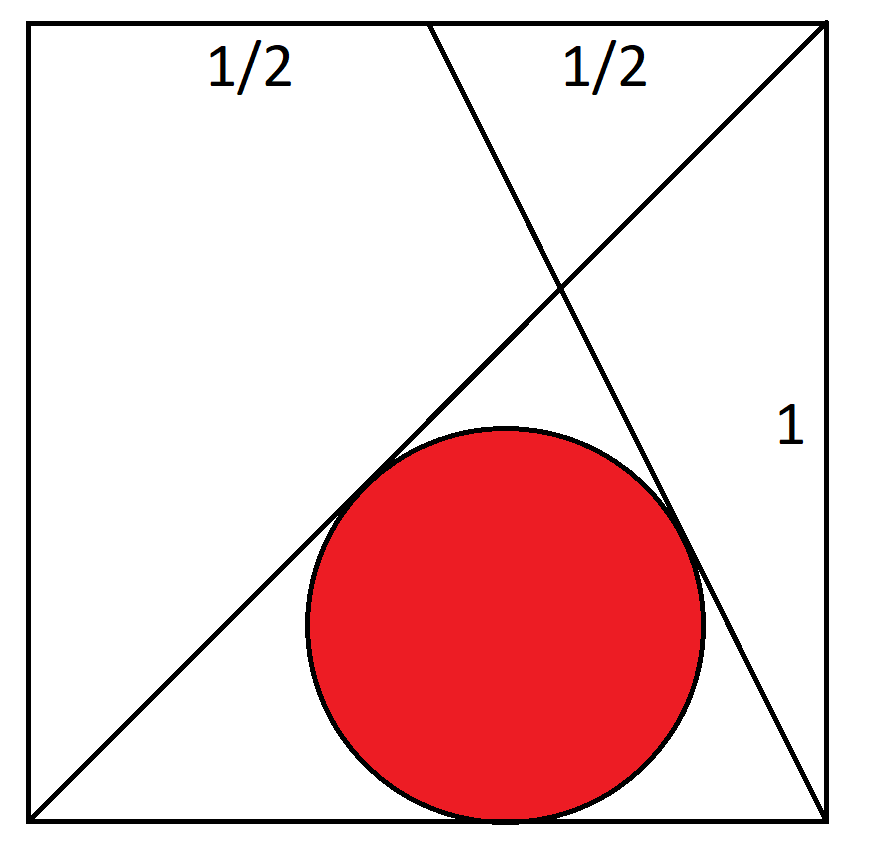
Este enigma foi publicado na edição de outubro de 2020 do Boletim da Mensa.

anônimo

tan(2x)=2tan(x)/(1-tan 2 (x))

A resposta é (1+sqrt(2)+sqrt(5)-sqrt(10))/6 = aproximadamente 0,248000646617418.

Aqui está minha solução (PDF).

Este problema é abordado e discutido no meu fórum, Wizard of Vegas .

Qual a probabilidade de conseguir um Yahtzee se essa for a única categoria restante no cartão?

anônimo

Para os leitores que não estão familiarizados com Yahtzee, a pergunta é qual a probabilidade de se obter uma combinação de cinco dados iguais em três lançamentos de cinco dados. Após cada lançamento, você deve escolher quais dados manter e quais lançar novamente.

A resposta é 4,6029%.

Aqui estão os possíveis resultados após o primeiro lançamento ou qualquer lançamento em que o jogador tire 4 ou 5 dados.

  • Cinco de um tipo = 6*(1/6)^5 = 0,000772
  • Quadra = (1/6)^3*(5/6)*4 = 0,015432
  • Três de um tipo = (1/6)^2*(5/6)^2*COMBIN(4,2) = 0,115741
  • Dois de um tipo = 4*(1/6)*(5/6)^3 = 0,385802
  • Único = 6*5!/6^5 = 0,092593

Aqui estão as probabilidades após segurar um par.

  • Cinco de um tipo = (1/6)^3 = 0,004630
  • Quadra = 3*(1/6)^2*(5/6) = 0,069444
  • Três de um tipo = 3*(1/6)*(5/6)^2+5*(1/6)^3 = 0,370370
  • Dois de um tipo = (5/6)^3 - 5*(1/6)^3 = 0,555555

Aqui estão as probabilidades após formar uma trinca:

  • Cinco de um tipo = (1/6)^3 = 0,002778
  • Quadra = 2*(1/6)*(5/6) = 0,27778
  • Três de um tipo = (5/6)^2 = 0,694444

Aqui estão as probabilidades após formar uma quadra:

  • Cinco de um tipo = 1/6 = 0,166667
  • Quadra = 5/6 = 0,83333

Com essas probabilidades de avanço, aqui estão as probabilidades de cada estado após a segunda rodada:

  • Cinco de um tipo = 0,000772 + 0,015432*0,166667 + 0,115741*0,002778 + 0,385802*0,004630 + 0,092593*0,000772 = 0,012631
  • Quadra = 0,015432*0,166667 + 0,115741*0,27778 + 0,115741*0,27778 = 0,116970
  • Três de um tipo = 0,115741*0,694444 + 0,385802*0,370370 + 0,092593*0,115741 = 0,409022
  • Dois de um tipo = 0,385802*0,555555 + 0,092593*0,385802 = 0,450103
  • Único = 0,092593 * 0,092593 = 0,008573

Usando as mesmas probabilidades de avanço, aqui está a probabilidade de um Yahtzee após o terceiro lançamento:

Cinco de um tipo = 0,012631 + 0,116970*(1/6) + 0,409022*(1/6)^2 + 0,450103*(1/6)^3 + 0,008573*(1/6)^4 = 0,046029.

Para aqueles que preferem álgebra matricial, existe a matriz de transição:

0,092593 0,694444 0,192901 0,019290 0,000772
0,000000 0,555556 0,370370 0,069444 0,004630
0,000000 0,000000 0,694444 0,277778 0,027778
0,000000 0,000000 0,000000 0,833333 0,166667
0,000000 0,000000 0,000000 0,000000 1.000000

Se a matriz acima for M, então o estado após três lançamentos será M 3 , como segue:

0,000794 0,256011 0,452402 0,244765 0,046029
0,000000 0,171468 0,435814 0,316144 0,076575
0,000000 0,000000 0,334898 0,487611 0,177491
0,000000 0,000000 0,000000 0,578704 0,421296
0,000000 0,000000 0,000000 0,000000 1.000000

A probabilidade de obter um Yahtzee após três lançamentos pode ser encontrada na célula no canto superior direito.

Depois de assistir a O Gambito da Rainha , notei que nenhuma das partidas na série terminou em empate. Eu pensava que o xadrez em alto nível tivesse muitos empates. Para o xadrez de nível grande mestre, qual a porcentagem de partidas que terminam em empate?

anônimo

De acordo com o artigo "O número de empates no xadrez aumentou?" no ChessBase.com, o autor Qiyu Zhou afirma que, em 78.468 partidas ranqueadas entre jogadores com rating de 2600 ou superior (são necessários 2500 pontos para ser um grande mestre), os resultados foram os seguintes:

  • Vitórias dos negros: 18,0%
  • Vitórias dos brancos: 28,9%
  • Empate: 53,1%