Pergunte ao Mago #336
O cassino Morongo , no sul da Califórnia, está com uma promoção em que paga um bônus de $16 se o crupiê receber um 16 rígido. Qual é o valor desse bônus?
Essa é uma boa opção para o jogador! O site deles não detalha as regras, então vou presumir que se aplica apenas às duas primeiras cartas. Vi em um antigo boletim informativo da Current Blackjack de outubro de 2018 que a maioria das mesas segue as seguintes regras:
- Concessionária atinge o nível 17
- Seis decks
- O Blackjack paga 3 para 2.
- Dobro após divisão permitido
- É permitido dividir ases novamente.
Minha calculadora de vantagem da casa no blackjack indica que essas regras têm uma vantagem da casa de 0,55% com um embaralhador contínuo e de 0,57% com uma carta de corte.
Independentemente das regras, a probabilidade de um 16 rígido nas duas primeiras cartas é de 6,51%. Receber $16 com uma probabilidade de 6,51% equivale a $1,04 por mão. Vou assumir uma aposta mínima de $25, pois a maioria dos cassinos está aumentando seus valores mínimos nesta era do coronavírus. Sem contar o bônus, a perda esperada por mão é de $0,14 com uma aposta de $25. Isso resulta em um ganho esperado por mão de $1,04 - $0,14 = $0,90. Em relação ao valor da aposta, isso representa uma vantagem para o jogador de 3,59%!
Se considerarmos um cenário ideal de jogar três mãos de $25 a 80 rodadas por hora, isso resultaria em um ganho esperado de $216 por hora!
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Há um tabuleiro de pinos 5x5 com 3 pinos. Qual é a probabilidade de que três pinos colocados aleatoriamente formem um triângulo?
Primeiro, existem combin(25,3) = 2.300 combinações possíveis para os pinos.
Quantas dessas combinações formam um triângulo? Vamos usar este tabuleiro para ajudar:
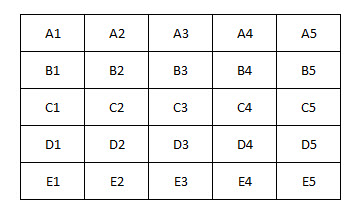
Primeiro, há cinco linhas, cinco colunas e duas diagonais. Para qualquer uma delas, há combin(5,3) = 10 maneiras de colocar os pinos em linha. Portanto, há 12*10 = 120 combinações dessa forma.
Em segundo lugar, existem quatro maneiras de conectar o quadrado central de uma linha/coluna ao quadrado central de uma linha/coluna adjacente. Em outras palavras, essas três posições:
- A3, B4, C5
- C5, D4, E3
- E3, D2, C1
- C1, B2, A3
Então, agora estamos com 120 + 4 = 124.
Terceiro, existem quatro linhas diagonais diferentes que representam quatro espaços:
- Lá2, Si3, Dó4, Ré5
- B5, C4, D3, E2
- E4, D3, C2, B1
- Ré1, Dó2, Si3, Lá4
Para cada um deles existem combin(4,3)=4 maneiras de colocar três pinos. Isso adiciona 4*4 = 16 a mais.
Agora estamos em 124 + 16 = 140
Em quarto lugar, considere a forma como os cavalos se movem no xadrez, num tabuleiro em forma de L de 2x1. Para cada vértice, existem duas maneiras pelas quais um cavalo pode se mover. Em todas elas, o cavalo pode se mover novamente na mesma linha formada pelo primeiro movimento. Portanto, são 4*2 = 8 movimentos adicionais:
- Lá1, Dó2, Mi3 Lá1, Si3, Dó5
- A5, B3, C1
- Lá5, Dó4, Mi3
- E5, C4, A3
- E5, D3, C1
- E1, D3, C5
- E1, C2, A3
Existem também quatro linhas de cavaleiros que atravessam o centro:
- Lá2, Dó3, Mi4
- Lá4, Dó3, Mi2
- B5, C3, D1
- Ré5, Dó3, Si1
Somando as 12 linhas de cavaleiros, chegamos a 140 + 12 = 152.
Se existem 2.300 combinações no total e 152 formam linhas, então 2.300 - 152 = 2.148 não formam linhas e, portanto, formam triângulos.
Assim, nossa resposta é 2.148/2.300 = 93,39%.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Encontrei um jogo de Spanish 21 com 4 baralhos que paga 3-2 em um ás/10 após dividir. Quanto vale essa regra?
Para simplificar, vamos assumir que dividir ases novamente não é permitido. Lembre-se também que o Spanish 21 usa baralhos espanhóis de 48 cartas, sem o valor 10. Por fim, lembre-se de que 21 pontos garantem a vitória automática no Spanish 21.
Mesmo sem essa regra, o jogador deve sempre dividir os ases. A probabilidade de obter um par de ases em um jogo com quatro baralhos espanhóis é combin(16,2)/combin(192,2) = 120/18336 = 0,65%.
A probabilidade de cada ás se transformar em 10 é (4*12)/(48*12-2) = 48/190 = 25,26%. Com dois ases, o número esperado de cartas que se transformarão em blackjack é 2*48/190 = 96/190 = 0,5053.
Cada blackjack valerá meia unidade extra. Assim, o valor desta regra é (120/18336)*(96/190)*(1/2) = 0,17%.
Mesmo com essa regra, o jogador ainda não deve dividir os dez, então não precisamos nos preocupar com isso. Portanto, essa regra reduz a vantagem da casa em 0,17%.
Quantos retângulos únicos existem em que o número de ladrilhos no perímetro é igual ao número de ladrilhos na parte interna?
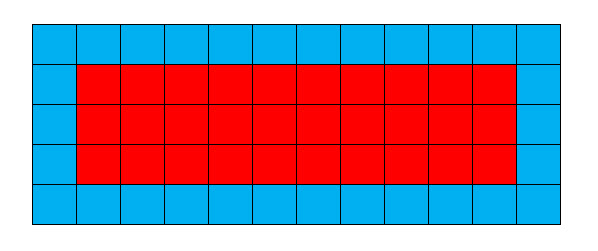
Vamos considerar x e y como as dimensões do retângulo INTERNO.
A área desse retângulo é x*y.
A área do perímetro é 2x + 2y + 4
É dado que xy = 2x + 2y + 4
xy - 2x = 2y + 4
x(y-2) = 2y+4
x=(2y+4)/(y-2)
y deve ser maior ou igual a 3. Vejamos qual é o valor de x para alguns valores de y iguais ou maiores que 3.
Se y = 3, então x = 10
Se y = 4, então x = 6
Se y = 5, então x = 14/3
Se y = 6, então x = 4
Portanto, 3x10 e 4x6 são soluções. 6x4 não é, porque não é uma solução única. Conforme y aumenta, x diminui. Assim como y deve ser igual ou maior que 3, x também deve ser. Há apenas mais um valor possível para x, já que ele diminui conforme y aumenta, que é x=3. No entanto, se x=3, então y=10, e esse valor também não é único.
Portanto, a resposta é 2: 3x10 e 4x6 para o retângulo interno. Se preferir contar as soluções pelo retângulo externo, elas seriam 5x12 e 6x8.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .


