Recomendações do Mago
-
Bônus de boas-vindas de $11000 -
Bônus de boas-vindas de 3000 $ -
BÔNUS DE ATÉ $777
Pergunte ao Mago #338
Qual é o número médio de lançamentos necessários com dois dados para obter qualquer total de 2 a 12?
Uma cadeia de Markov poderia ser usada para responder a essa pergunta, mas eu prefiro o cálculo diferencial e integral. A questão principal é que a resposta é a mesma se o intervalo de tempo entre os lançamentos seguir uma distribuição exponencial com média igual a um. Dito isso, a resposta pode ser expressa como a integral de 0 ao infinito de:
1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))
Você pode resolver facilmente essas integrais com uma calculadora de integrais .
Você também pode resolver qualquer problema desse tipo com a minha Calculadora de Ensaios Esperados .
Há uma formiga no centro de um quadrado. Ela está a 17 polegadas do canto superior esquerdo, a 20 polegadas do canto superior direito e a 13 polegadas do canto inferior direito.
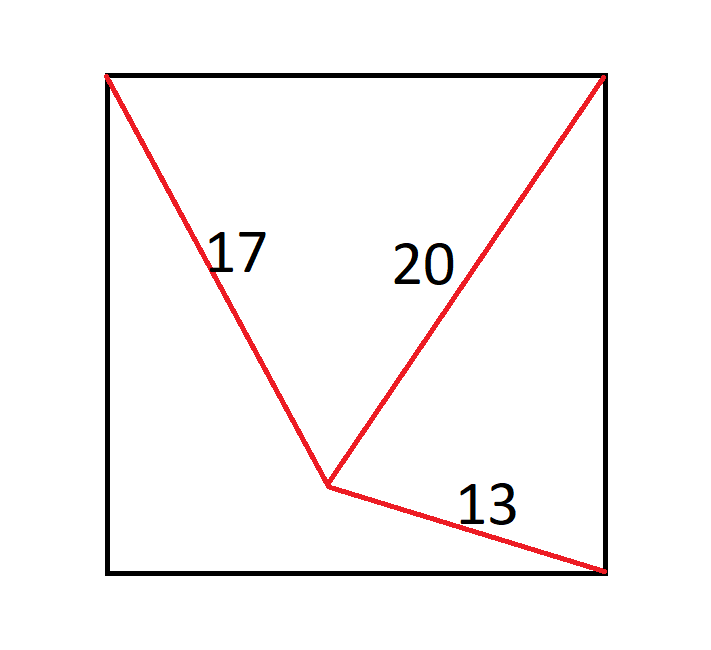
Qual o tamanho do quadrado?
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
Primeiro, gire o triângulo ABE 90 graus para formar um novo triângulo BDF.
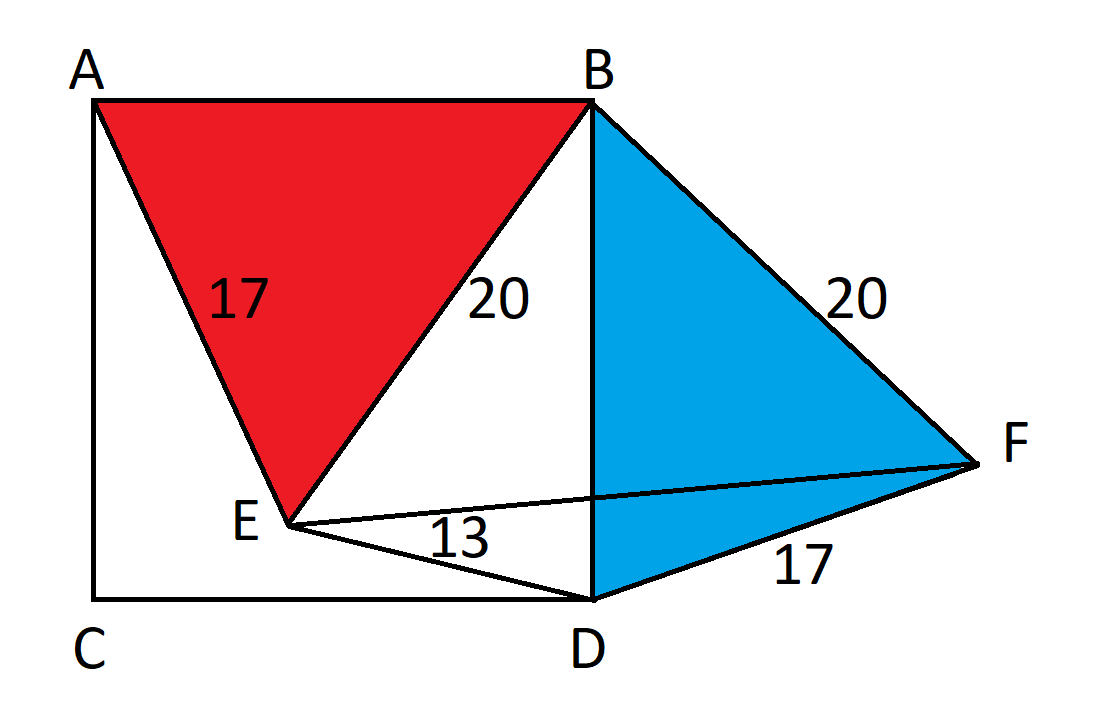
Como o triângulo foi rotacionado 90 graus, o ângulo EBF = 90, por definição. Pela fórmula de Pitágoras, EF = 20*sqrt(2).
Pela lei dos cossenos: 17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF).
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680.
cos(DEF) = 17*sqrt(2)/26.
Lembre-se, sin^2(x) + cos^2(x) = 1. Vamos usar isso para resolver para sin(DEF).
sen²(DEF) + cos²(DEF) = 1
sen²(DEF) + (17√2/26)² = 1
sen²(DEF) + 289/338 = 1
sen²(DEF) = 49/338
sen(DEF) = 7*sqrt(2)/26
Em seguida, considere o ângulo BED.
Ângulo BED = Ângulo BEF + Ângulo FED.
Sabemos que o ângulo EBF mede 90 graus e que o triângulo é isósceles. Isso faria com que o ângulo BEF medisse 45 graus.
Portanto, o ângulo da cama (BED) é igual a 45 graus mais o ângulo de alimentação (FED).
Lembre-se, cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/m²(2))*17*m²(2)/26 - (1/m²(2))*7*m²(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
Vamos aplicar novamente a lei dos cossenos, desta vez ao triângulo BED.
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD é o lado do quadrado em questão, portanto BD^2 é a área desse quadrado, que mostramos ser 369.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Drop Dead é um jogo jogado com cinco dados padrão. Você começa sua vez rolando os cinco dados. Se nenhum deles for 2 ou 5, você soma os dados, adiciona a soma à sua pontuação e rola novamente. Se você rolar algum 2 ou 5, sua pontuação para a rolagem é zero. Todos os dados que mostrarem 2 ou 5 são considerados mortos e descartados. Você então rola novamente com os dados restantes. O jogo continua com você marcando pontos ou descartando dados. Sua vez termina quando todos os seus dados forem eliminados, momento em que se diz que você "morreu". Todas as suas pontuações são somadas para obter sua pontuação final. Quem tiver a maior pontuação vence.
Qual é a sua expectativa de pontuação para este jogo?
Vamos começar com o cenário em que resta apenas um dado e prosseguir para trás.
Seja a variável a quantidade de pontos adicionais esperados com um dado restante.
A média dos resultados que não são 2 ou 5 é (1+3+4+6)/4 = 7/2.
a = (2/3)×(a + 7/2).
a/3 = 7/3.
a = 7.
Em seguida, vamos calcular b, a pontuação esperada com dois dados restantes.
b = (2/3) 2 ×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a.
b = 11,2.
Em seguida, vamos calcular c, a pontuação esperada com três dados restantes.
c = (2/3) 3 ×(c + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×b + 3×(2/3)×(1/3) 2 ×b.
c = 1302/95 = 13,705263.
Em seguida, vamos calcular d, a pontuação esperada com quatro dados restantes.
d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a.
d = 3752/247 = 15,190283.
Por fim, vamos calcular e, a pontuação esperada com cinco dados restantes.
e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×a.
e = 16,064662.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Considere a aposta Pairplus no Three Card Poker, que segue a tabela de pagamento 1-4-6-30-40. No entanto, ela paga um jackpot para um mini-royal de espadas e 25% desse jackpot para um mini-royal nos outros três naipes. Qual deveria ser o valor mínimo para que a aposta seja considerada justa?
A resposta é 384 vezes o valor da aposta.
Para cada 100 apostas adicionais acima desse valor, o retorno aumenta em 0,79%.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .