WOO logo

Recomendações do Mago

Pergunte ao Mago #340

Se um cassino aumentasse a probabilidade de ganho na aposta "Empate" para 9 para 1, acima da probabilidade usual de 8 para 1, quanto a mais de apostas ele precisaria fazer no "Empate" para obter o mesmo ganho esperado?

dandolos2000

A probabilidade de um empate no bacará é de 0,095155968.

Na vitória usual de 8 para 1, o retorno esperado para o jogador é 0,095156 × (8+1) - 1 = -0,143596.

Com uma vitória de 9 para 1, o retorno esperado para o jogador é 0,095156 × (9+1) - 1 = --0,048440.

A perda esperada do jogador é 0,143596/0,048440 = 2,9643960 vezes maior com uma probabilidade de vitória de 8 para 1. Portanto, o cassino precisaria de 2,9643960 vezes mais apostas no empate se aumentasse a probabilidade de vitória para 9 para 1 para que o ganho esperado do cassino fosse o mesmo.

Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .

Suponha que haja uma caixa com 100 bolas, numeradas de 1 a 100. Dez bolas são retiradas aleatoriamente, sem reposição. Qual é o número médio da bola de menor valor retirada?

ThatDonGuy

A tabela a seguir mostra o número de combinações, a probabilidade e a contribuição para a bola mais baixa (produto da bola e da probabilidade). A célula inferior direita mostra que a bola mais baixa esperada é 9,1818182.

Bola mais baixa

Mais baixo
Bola		 Combinações Probabilidade Esperado
Proposta baixa
1 1.731.030.945.644 0,100000 0,100000
2 1.573.664.496.040 0,090909 0,181818
3 1.429.144.287.220 0,082560 0,247681
4 1.296.543.270.880 0,074900 0,299600
5 1.174.992.339.235 0,067878 0,339391
6 1.063.677.275.518 0,061448 0,368686
7 961.835.834.245 0,055564 0,388950
8 868.754.947.060 0,050187 0,401497
9 783.768.050.065 0,045278 0,407498
10 706.252.528.630 0,040800 0,407995
11 635.627.275.767 0,036720 0,403915
12 571.350.360.240 0,033006 0,396076
13 512.916.800.670 0,029631 0,385199
14 459.856.441.980 0,026565 0,371917
15 411.731.930.610 0,023785 0,356780
16 368.136.785.016 0,021267 0,340271
17 328.693.558.050 0,018988 0,322801
18 293.052.087.900 0,016929 0,304728
19 260.887.834.350 0,015071 0,286354
20 231.900.297.200 0,013397 0,267933
21 205.811.513.765 0,011890 0,249680
22 182.364.632.450 0,010535 0,231771
23 161.322.559.475 0,009319 0,214347
24 142.466.675.900 0,008230 0,197524
25 125.595.622.175 0,007256 0,181388
26 110.524.147.514 0,006385 0,166007
27 97.082.021.465 0,005608 0,151425
28 85.113.005.120 0,004917 0,137673
29 74.473.879.480 0,004302 0,124766
30 65.033.528.560 0,003757 0,112708
31 56.672.074.888 0,003274 0,101491
32 49.280.065.120 0,002847 0,091100
33 42.757.703.560 0,002470 0,081512
34 37.014.131.440 0,002138 0,072701
35 31.966.749.880 0,001847 0,064634
36 27.540.584.512 0,001591 0,057276
37 23.667.689.815 0,001367 0,050589
38 20.286.591.270 0,001172 0,044534
39 17.341.763.505 0,001002 0,039071
40 14.783.142.660 0,000854 0,034160
41 12.565.671.261 0,000726 0,029762
42 10.648.873.950 0,000615 0,025837
43 8.996.462.475 0,000520 0,022348
44 7.575.968.400 0,000438 0,019257
45 6.358.402.050 0,000367 0,016529
46 5.317.936.260 0,000307 0,014132
47 4.431.613.550 0,000256 0.012032
48 3.679.075.400 0,000213 0,010202
49 3.042.312.350 0,000176 0,008612
50 2.505.433.700 0,000145 0,007237
51 2.054.455.634 0,000119 0,006053
52 1.677.106.640 0,000097 0,005038
53 1.362.649.145 0,000079 0,004172
54 1.101.716.330 0,000064 0,003437
55 886.163.135 0,000051 0,002816
56 708.930.508 0,000041 0,002293
57 563.921.995 0,000033 0,001857
58 445.891.810 0,000026 0,001494
59 350.343.565 0,000020 0,001194
60 273.438.880 0,000016 0,000948
61 211.915.132 0,000012 0,000747
62 163.011.640 0,000009 0,000584
63 124.403.620 0,000007 0,000453
64 94.143.280 0,000005 0,000348
65 70.607.460 0,000004 0,000265
66 52.451.256 0,000003 0,000200
67 38.567.100 0,000002 0,000149
68 28.048.800 0,000002 0,000110
69 20.160.075 0,000001 0,000080
70 14.307.150 0,000001 0,000058
71 10.015.005 0,000001 0,000041
72 6.906.900 0,000000 0,000029
73 4.686.825 0,000000 0,000020
74 3.124.550 0,000000 0,000013
75 2.042.975 0,000000 0,000009
76 1.307.504 0,000000 0,000006
77 817.190 0,000000 0,000004
78 497.420 0,000000 0,000002
79 293.930 0,000000 0,000001
80 167.960 0,000000 0,000001
81 92.378 0,000000 0,000000
82 48.620 0,000000 0,000000
83 24.310 0,000000 0,000000
84 11.440 0,000000 0,000000
85 5.005 0,000000 0,000000
86 2.002 0,000000 0,000000
87 715 0,000000 0,000000
88 220 0,000000 0,000000
89 55 0,000000 0,000000
90 10 0,000000 0,000000
91 1 0,000000 0,000000
Total 17.310.309.456.440 1.000000 9.181818

Existe uma maneira mais fácil de resolver problemas como este, onde a bola de menor valor é 1. A fórmula para a bola de menor valor é (m+1)/(b+1), onde m é o valor máximo da bola e b é o número de bolas. Neste caso, m=100 e n=10, então a bola de menor valor é 101/11 = 9,181818.

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .

O seguinte enigma foi publicado no New York Times em 6 de março de 2021.

As regras são bem simples:

  1. Cada linha, coluna e região deve ter exatamente duas estrelas.
  2. Duas estrelas não podem se tocar, nem mesmo na diagonal.

Você pode me ajudar a encontrar uma solução?

anônimo

Este é um quebra-cabeça chamado "Dois que não se tocam". O botão abaixo mostra minha resposta e solução.

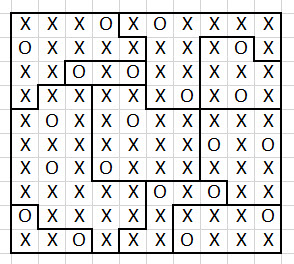
dois não se tocam resolvido

Aqui está minha solução (PDF).

Qual é o número esperado de lançamentos de um dado honesto de seis lados para que qualquer um dos lados seja lançado seis vezes?

Ace2

Clique no botão abaixo para ver minha resposta.

A resposta é 2597868106693535971 / 131621703842267136 = Aproximação: 19,73738396371749

Aqui está minha solução (PDF).