Pergunte ao Mago #341
Qual é o número esperado de lançamentos de dois dados para se obter qualquer total de 2 a 12? Por favor, utilize cálculo para sua resposta.
Lembre-se que a probabilidade de rolar um total de 2 é 1/36. Em t lançamentos, o número esperado de lançamentos com um total de 2 é t/36. Suponha que o tempo entre os lançamentos seja distribuído exponencialmente com uma média de t/36. A distribuição de Poisson nos diz que a probabilidade de zero lançamentos com um total de 2 é exp(-t/36).
Lembre-se que a probabilidade de rolar um total de 3 é 2/36 = 1/18. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 3 é exp(-t/18).
Lembre-se que a probabilidade de rolar um total de 4 é 3/36 = 1/12. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 4 é exp(-t/12).
Lembre-se que a probabilidade de rolar um total de 5 é 4/36 = 1/9. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 5 é exp(-t/9).
Lembre-se que a probabilidade de rolar um total de 6 é 5/36. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 6 é exp(-5t/36).
Lembre-se que a probabilidade de rolar um total de 7 é 6/36 = 1/6. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 7 é exp(-t/6).
As probabilidades de 8 a 12 são as mesmas que as de 2 a 6.
Assim, a probabilidade de que em t unidades de cada total tenha sido rolado pelo menos uma vez é:
(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
A probabilidade de que pelo menos o total NÃO tenha sido rolado em t unidades de tempo é 1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
Para obter o tempo esperado sem pelo menos um total, integramos a função acima de 0 ao infinito.
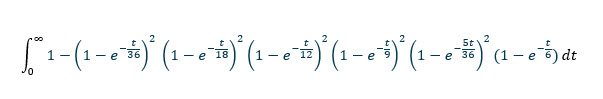
Uma calculadora de integrais (recomendo esta ) resolverá facilmente isso como 769767316159/12574325400 = aproximadamente 61,2173847639572 rolos.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Lance dois dados, um vermelho e um azul, repetidamente. Anote a soma dos lançamentos para cada dado. Qual é o número esperado de lançamentos até que os dois totais acumulados sejam iguais?
É difícil explicar por que a resposta é infinito. Para tornar as coisas ainda mais confusas e paradoxais, a probabilidade de os totais serem iguais em algum momento é 1.
A tabela a seguir mostra a probabilidade de os totais serem iguais pela primeira vez após 1 a 16 lançamentos.
Probabilidade de totais iguais para a primeira vez
| Rolls | Probabilidade |
|---|---|
| 1 | 0,166667 |
| 2 | 0,112654 |
| 3 | 0,092850 |
| 4 | 0,080944 |
| 5 | 0,072693 |
| 6 | 0,066539 |
| 7 | 0,061722 |
| 8 | 0,057819 |
| 9 | 0,054573 |
| 10 | 0,051819 |
| 11 | 0,049443 |
| 12 | 0,047367 |
| 13 | 0,045532 |
| 14 | 0,043895 |
| 15 | 0,042423 |
| 16 | 0,041089 |
O Excel mostra que um ajuste muito próximo a esta curva é y = 0,1784*x-1,011, onde x = número de lançamentos e y = probabilidade.
A soma dessa série infinita é infinita.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Qual é o valor do prêmio mínimo para o jogo Pennsylvania Cash 5 ? Desconsidere impostos e a divisão do prêmio.
Primeiro, vamos revisar as regras. O valor da aposta é de $2. O jogo consiste em sortear cinco bolas dentre 43. Aqui está a tabela de pagamentos:
- Acerto 5 = Prêmio máximo
- Matemática 4 = $200
- Combine 3 e ganhe $10
- Acerto 2 = $2
Além disso, o jogador recebe o que presumo ser um cartão raspadinha. Este cartão tem 1/80 de chance de pagar $6 e 1/5 de chance de pagar $2.
A tabela a seguir mostra minha análise do jogo base. Ela demonstra que o valor de acertar de 2 a 4 números é de $0,287784.
Tabela de Retorno de Dinheiro 5
| Pegar | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| 5 | prêmio máximo | 1 | 0,000001 | ? |
| 4 | 200 | 190 | 0,000197 | 0,039477 |
| 3 | 10 | 7030 | 0,007303 | 0,073032 |
| 2 | 2 | 84360 | 0,087638 | 0,175276 |
| 1 | 0 | 369075 | 0,383416 | 0,000000 |
| 0 | 0 | 501942 | 0,521445 | 0,000000 |
| Total | 0 | 962598 | 1.000000 | 0,287784 |
A tabela a seguir mostra minha análise do recurso de prêmio instantâneo Quick Cash. A célula inferior direita mostra um valor de $0,475.
Tabela de Retorno Imediato de Dinheiro
| Pegar | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 6 | 1 | 0,012500 | 0,075000 |
| 2 | 16 | 0,200000 | 0,400000 |
| 0 | 63 | 0,787500 | 0,000000 |
| Total | 80 | 1.000000 | 0,475000 |
Assim, o valor dos prêmios não progressivos é de $0,287784 + $0,475000 = $0,762784.
Seja j o valor do prêmio acumulado de equilíbrio. Então:
2 = 0,762784 + j × (1/962598)
1,237216 = j × (1/962598)
j = 1,237216 × 962598
j = $ 1.190.941,95.
A taxa de retorno total é de 0,381392 mais 0,051943 para cada US$ 100.000 no prêmio acumulado.
Conforme mencionado na pergunta, tudo isso ignora impostos e a divisão do prêmio principal.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .


