WOO logo

Recomendações do Mago

Pergunte ao Mago #349

No diagrama a seguir, qual é a área da região azul?

anônimo

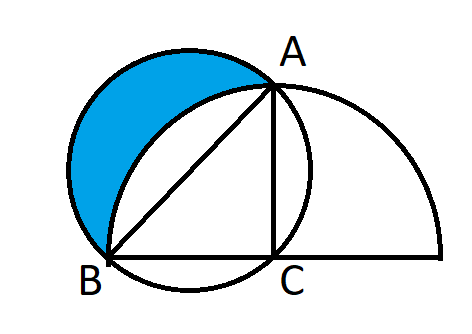
Clique no botão abaixo para ver a resposta.

1/2

Aqui está minha solução (PDF).

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .

Qual é o número médio de cartas que o jogador mantém após o descarte no vídeo pôquer?

anônimo

A tabela a seguir mostra o número médio de cartas na mão em 10 jogos diferentes e suas respectivas tabelas de pagamento. A média dos jogos listados é 2,05.

Número médio de cartas na mão no vídeo pôquer

Jogo Tabela de Pagamento Retornar Av. Cartões Segurados
Bônus Dois 10-4-3-3 97,36% 1,845550
Deuces Wild 25-15-9-5-3 100,76% 1,926010
Ás em chamas 9-5 99,57% 2,055630
Super Duplo Duplo Bônus 7-5 99,17% 2,057280
Bônus Duplo Duplo 9-5 97,87% 2,058390
Bônus Triplo Duplo 8-5 95,97% 2.072620
Bônus Poker 8-5 99,17% 2.080610
Valetes ou Melhor 9-5 98,45% 2.081030
Bônus Poker Deluxe 8-5 97,40% 2,150470
Bônus Duplo 9-6-5 97,81% 2,173550

Em um torneio de xadrez, cada participante joga uma partida contra todos os outros. Cada participante recebe 1 ponto por cada partida que vence, 0,5 pontos por cada partida empatada e 0 pontos por cada partida que perde.

Ao final do torneio, constatou-se que todos os competidores obtiveram números diferentes de pontos e o último colocado na classificação derrotou cada um dos três primeiros colocados.

Assim sendo, qual é o número mínimo de competidores que participam do torneio?

Gialmere

13

Vamos chamar o número de jogadores de n.

Considero que o jogador em último lugar tem apenas três vitórias, contra os 3 melhores jogadores, e perdeu todas as outras partidas. Isso lhe dá 3 pontos.

Em seguida, considero que cada jogador subsequente, em ordem de pontos, tem 0,5 pontos a mais que o anterior, na classificação. Isso daria ao jogador de classificação mais alta 3+(n-1)/2 pontos.

Fazendo a soma de 3 com 3+(n-1)/2, por 1/2 ponto por passo, obtemos (((n+5)*(n+6)/2)-15)/2.

O número total de partidas jogadas com n jogadores é n*(n-1)/2, onde cada jogador joga contra todos os outros uma vez. Cada partida resulta em um ponto, que também é o total de pontos ganhos por todos os jogadores.

Em seguida, resolva para n:

(((n+5)*(n+6)/2)-15)/2 = n*(n-1)/2
((n+5)*(n+6)/2)-15 = n*(n-1)
(n+5)*(n+6)/2 = n*(n-1) + 15
(n+5)*(n+6) = 2*n*(n-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
n² + 11n = 2n² - 2n
n + 11 = 2n-2
n=13

A tabela a seguir mostra uma maneira pela qual isso pode acontecer. O corpo da tabela mostra o vencedor em todos os 78 jogos.

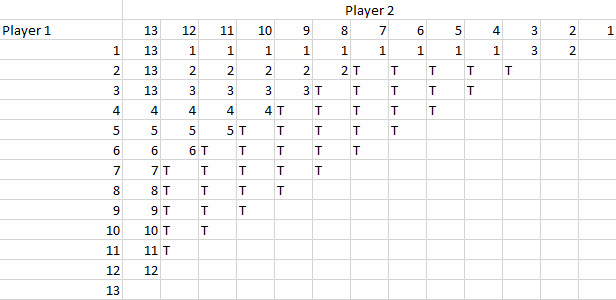
A tabela a seguir mostra o número de pontos de cada jogador.

Total de pontos por jogador

Jogador Pontos
13 3
12 3,5
11 4
10 4.5
9 5
8 5.5
7 6
6 6,5
5 7
4 7,5
3 8
2 8,5
1 9

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .