Recomendações do Mago
-
Bônus de boas-vindas de $11000 -
Bônus de boas-vindas de 3000 $ -
BÔNUS DE ATÉ $777
Pergunte ao Mago #351
O que você acha dessa estratégia na roleta?
- Aposte duas unidades no preto.
- Aposte uma unidade na terceira coluna.
A beleza dessa estratégia reside no fato de haver 8 números vermelhos e 4 números pretos na terceira coluna. Dos 16 números vermelhos, metade está nas colunas 1 ou 2 e a outra metade na coluna 3. Vamos ignorar o 0 e o 00 por enquanto. Quando a bola cai no vermelho, 8 dos 18 números vermelhos estão na terceira coluna. Se a probabilidade de ganhar é de 8/18 e os ganhos pagam 2 para 1, tenho uma vantagem de 33,3%. Mesmo se fizermos a média com a aposta no preto, que tem 0% de vantagem da casa, e ignorando novamente o 0 e o 00 por enquanto, ainda tenho uma vantagem de 16,7%. Incluindo o 0 e o 00, minha vantagem não seria (2/38)*-100% + (36/38)*16,7% = 10,53%? O que você acha?
Concordo que a vantagem condicional da aposta na terceira coluna é de 33,3%, assumindo que a bola caia no vermelho e ignorando os dois zeros. No entanto, pela mesma lógica, se a bola cair no preto, a probabilidade de a aposta na terceira coluna ganhar é de 4/18 = 2/9. Uma aposta com 2/9 de chance de ganhar que paga 2 para 1 teria uma vantagem da casa de 33,33%. Portanto, considerando sua perspectiva, a aposta na terceira coluna teria uma vantagem do jogador de 33,33% metade das vezes e uma vantagem da casa de 33,33% na outra metade. Cancelando-se mutuamente, essa aposta tem 0% de vantagem da casa. Finalmente, considerando os dois zeros, a vantagem total do jogador é de (2/38)*-100% + (36/38)*0% = -5,26%.
Analisando de outra forma, a tabela a seguir mostra o número de maneiras pelas quais todos os resultados possíveis podem ocorrer, a probabilidade, as unidades ganhas e a contribuição para o retorno. A célula inferior direita mostra uma perda esperada de -0,105263 unidades. Dividindo isso pelas duas unidades apostadas, chega-se a uma vantagem da casa de 5,26%.
Estratégia da Boêmia
| Evento | Paga | Números | Probabilidade | Retornar |
|---|---|---|---|---|
| 0, 00 | -2 | 2 | 0,052632 | -0,105263 |
| Vermelho e coluna 1 ou 2 | -2 | 10 | 0,263158 | -0,526316 |
| Vermelho e coluna 3 | 1 | 8 | 0,210526 | 0,210526 |
| Preto e coluna 1 ou 2 | 0 | 14 | 0,368421 | 0,000000 |
| Preto e coluna 3 | 3 | 4 | 0,105263 | 0,315789 |
| Total | 38 | 1.000000 | -0,105263 |
Nos cassinos de Las Vegas, as cores das fichas para apostas de até US$ 100 são bem conhecidas, conforme segue:
- $1 = Branco ou azul
- $5 = Vermelho
- $ 25 = Verde
- $100 = Preto
Minha pergunta é: quais são as cores disponíveis para fichas acima de 100 dólares?
A maioria dos cassinos usa roxo para fichas de $500 e amarelo para fichas de $1.000. Além disso, as coisas não são tão padronizadas. É fácil dizer que laranja e marrom são populares, mas nem todos seguem essa convenção. Às vezes, vemos branco e azul ressurgindo. Pode-se argumentar que essas cores já eram usadas para fichas de $1, mas os valores das fichas aumentam a partir de um certo ponto, geralmente em $1.000. A tabela a seguir mostra o que eu sei.
Cores dos chips
| Cassino | $ 5.000 | $ 25.000 | $ 100.000 |
|---|---|---|---|
| Resorts World | Marrom | Laranja | |
| Cosmopolita | Branco | Laranja | |
| Ilha do Tesouro | Branco | ||
| Palazzo/Veneziano | Marrom | Laranja | Cinza/marrom |
| Rancho Green Valley | Marrom | ||
| Cerca de | Laranja | ||
| Wynn | Branco/vermelho | Marrom | |
| Bellagio | Branco | Laranja | Azul aço |
| Pepita de Ouro | Vermelho, branco e azul |
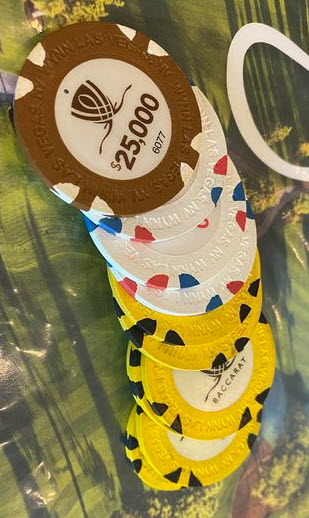
Gostaria de agradecer a Mdawg pela ajuda com esta questão e pelas imagens.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Você viu esse vídeo de um jogador que acertou o flop, o turn e o river no Texas Hold'em? Quais são as chances?
No flop, o jogador anuncia 8-9-10. Observe que ele não especifica os naipes. Tudo o que ele sabe é que desistiu de um valete e uma dama. O número de maneiras de um 8, 9 e 10 aparecerem no flop é 4*4*4 = 64. Restam 50 cartas desconhecidas no baralho. O número de maneiras de escolher três cartas dentre 50 é combin(50,3) = 19.600. Portanto, a probabilidade de acertar o flop era de 64/19.600 = 1 em 306,25.
Na rodada seguinte, restam 47 cartas desconhecidas no baralho. Ele acerta o 4 de espadas, que tinha uma chance em 47 de estar correto.
No river, restam 46 cartas desconhecidas no baralho. Ele acerta o dois de copas, que tinha uma chance em 46 de estar certo.
A probabilidade de acertar todas as três previsões foi (46/19600) × (1/47) × (1/46) = 1 em 662.113.
O que eu pessoalmente acho? Pura sorte. Vejo palpites errados nas mesas de jogo o tempo todo. Você acha que alguém faz um vídeo no YouTube com os milhões de palpites errados que foram rapidamente esquecidos? Em outras palavras, estou decepcionado.