Pergunte ao Mago #352
Em quanto os pagamentos máximos aumentam a vantagem da casa no Mississippi Stud?
Boa pergunta. Os jogadores de Mississippi Stud definitivamente devem estar cientes de que os pagamentos máximos podem reduzir o que eles ganham com um Royal Flush, o que aumenta a vantagem da casa.
No Mississippi Stud, o pagamento máximo é de 500 para 1 para um Royal Flush e se aplica a todas as apostas. O jogador tem duas chances de aumentar a aposta em até 3x o valor do Ante, então sua aposta final pode ser de até 7x o valor do Ante. Se o jogador espera um Royal Flush, ele deve maximizar os aumentos permitidos.
Em Mississippi Stud, o máximo que um jogador deve apostar no Ante, sem ser afetado por um limite de pagamento, é o pagamento máximo dividido por 3500. Por exemplo, se o pagamento máximo for de $80.000, o máximo que eu recomendo apostar no Ante é $22,86. Eu arredondaria esse valor para $20.
A tabela a seguir mostra a vantagem da casa em várias apostas e ganhos máximos comuns. A tabela pressupõe uma estratégia ótima do jogador, sem limite de ganhos. Observe como a vantagem da casa aumenta à medida que o valor da aposta aumenta e o limite diminui.
Vantagem da casa com limite de pagamento
| Aposta | Limite de $50.000 | Limite de US$ 80.000 | Limite de US$ 100.000 |
|---|---|---|---|
| $ 15 | 5,02% | 4,91% | 4,91% |
| $ 20 | 5,15% | 4,91% | 4,91% |
| $ 25 | 5,22% | 5,04% | 4,91% |
| $ 50 | 5,38% | 5,28% | 5,22% |
| $ 75 | 5,49% | 5,37% | 5,33% |
| $ 100 | 5,64% | 5,41% | 5,38% |
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
O site Vital Vegas repreendeu um jogador por dar uma gorjeta de apenas US$ 200 em um prêmio de US$ 1,1 milhão. Qual é a etiqueta apropriada para dar gorjeta em uma situação como essa?
Sim, embora critiquem o jogador pela pequena gorjeta, convenientemente evitam a pergunta sobre qual seria uma gorjeta apropriada.
A etiqueta das gorjetas não está bem definida apenas para grandes prêmios, como também para os pequenos. As opiniões são muito diversas, muitas delas vindas de pessoas que nunca ganharam um prêmio na loteria.
Primeiramente, gostaria de enfatizar que dar gorjeta não é opcional. Espera-se que você dê gorjeta em um cassino pelo serviço recebido, de acordo com o valor ganho e o nível de serviço. É fácil se tornar o Sr. Pink neste ponto e racionalizar por que não se deve dar gorjeta por nada. O sistema de gorjetas é definitivamente falho, mas é o sistema que temos. Se você não concorda e se recusa a dar gorjeta, então não peça o serviço pelo qual se espera que se dê gorjeta.
Em segundo lugar, uma vez estabelecido que o jogador deve dar gorjeta ao ganhar o jackpot, qual o valor? Estou limitando esta discussão ao tipo de situação em que o jogador ganha apenas um jackpot. As regras são diferentes se o jogador ganhar vários, o que é normal em níveis de apostas muito altos. Lembre-se, as regras para preencher a documentação do jackpot são:
- Ganhar $1.200 ou mais em "caça-níqueis".
- Ganhar $1.500 ou mais no keno.
- Ganhar US$ 5.000 ou mais em um torneio de pôquer.
- Ganhar $600 ou mais E pelo menos 300 vezes o valor da aposta em jogos de mesa.
Qual a minha recomendação de gorjeta? No passado, eu costumava dizer de 0,5% a 2% do prêmio, sendo que quanto maior o prêmio, menor a porcentagem. No entanto, na época, eu não estava pensando em prêmios tão grandes. Essa faixa de valores me parece apropriada até cerca de US$ 100.000.
Essa questão me levou a criar uma fórmula específica, que acredito ser adequada para qualquer prêmio acumulado, de US$ 1.200 a milhões. Aqui está ela:
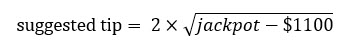
Se você não consegue ver a imagem, ela é 2×sqrt(jackpot-$1100).
Aqui está o que a fórmula fornece para alguns valores comuns de prêmios acumulados.
Tabela de gorjetas sugeridas
| Jackpot | Dica |
|---|---|
| $ 1.200 | $ 20 |
| $ 2.000 | $ 60 |
| $ 5.000 | $ 125 |
| US$ 10.000 | $ 189 |
| $ 20.000 | $ 275 |
| $ 50.000 | $ 442 |
| $ 100.000 | $ 629 |
| US$ 1.000.000 | $ 1.999 |
No caso de US$ 1,1 milhão, minha fórmula sugere US$ 2.096,57. Acho que arredondar para baixo, para US$ 2.000, não tem problema. Claro, também é preciso considerar outros fatores, como a qualidade do serviço.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Para um dado número grande, qual é a distância média entre os números primos próximos a esse número? Além disso, quantos números primos são menores que esse número?
Uma estimativa muito boa para a distância média entre primos próximos de qualquer número grande n é ln(n). É notável o quão bom é esse estimador.
Como evidência, a tabela a seguir mostra a amplitude dos primeiros 15 milhões de números primos, em grupos de um milhão. A tabela mostra a distância média entre os números primos dentro desse intervalo, bem como a estimativa dessa distância média. A estimativa é o logaritmo natural da média entre o maior e o menor número primo no intervalo. Por exemplo, para o 15º grupo de um milhão de números primos, a estimativa é ln((256.203.221 + 275.604.541)/2).
Distância média entre números primos
| Primeiro Prime em alcance | Último Prime em alcance | Números primos em alcance | Distância média | Estimativa | |
|---|---|---|---|---|---|
| 2 | 15.485.863 | 1.000.000 | 15,485861 | 15,86229105 | |
| 15.485.867 | 32.452.843 | 1.000.000 | 16,966976 | 16,9922867 | |
| 32.452.867 | 49.979.687 | 1.000.000 | 17,52682 | 17,53434381 | |
| 49.979.693 | 67.867.967 | 1.000.000 | 17,888274 | 17,89175615 | |
| 67.867.979 | 86.028.121 | 1.000.000 | 18.160142 | 18.15864108 | |
| 86.028.157 | 104.395.301 | 1.000.000 | 18.367144 | 18,3716137 | |
| 104.395.303 | 122.949.823 | 1.000.000 | 18,55452 | 18,54883262 | |
| 122.949.829 | 141.650.939 | 1.000.000 | 18.70111 | 18.70058553 | |
| 141.650.963 | 160.481.183 | 1.000.000 | 18.83022 | 18,83322787 | |
| 160.481.219 | 179.424.673 | 1.000.000 | 18,943454 | 18.95103217 | |
| 179.424.691 | 198.491.317 | 1.000.000 | 19.066626 | 19.05703535 | |
| 198.491.329 | 217.645.177 | 1.000.000 | 19,153848 | 19,15337672 | |
| 217.645.199 | 236.887.691 | 1.000.000 | 19.242492 | 19,24163365 | |
| 236.887.699 | 256.203.161 | 1.000.000 | 19.315462 | 19.32305683 | |
| 256.203.221 | 275.604.541 | 1.000.000 | 19.40132 | 19,39864545 |
Fonte: As lacunas entre os preços Prime no Prime Pages.
Para obter o número de números primos menores que qualquer número dado, podemos começar integrando a estimativa da distância média de ln(n). Isso nos dará a soma das distâncias médias entre números primos até qualquer número n.
Qual é a integral de f(n)=ln(n)? Lembre-se que a integração por partes nos diz:
Integral de f(n)*g'(n) dn = f(n)*g(n) - integral de (f'(n)*g(n)) dn
Sejam f(n)=ln(n) e g'(n)=1. Então f'(n)=1/n e g(n)=n. A integral de ln(n) será, portanto, ln(n)*n - integral de ((1/n)*n) = ln(n)*n - n = n*(ln(n)-1)
Se dividirmos n*(ln(n)-1) por n, obtemos a distância média entre primos no intervalo de números de 2 a n. Isso é ln(n)-1.
Se dividirmos n por essa distância média entre primos, obtemos o número médio de primos menores que n, que é igual a n/(ln(n)-1).
Como prova, a tabela a seguir mostra o número de números primos sob vários números grandes e o valor estimado. Peço desculpas pela precisão de 15 dígitos significativos, que é o máximo que o Excel permite. Alguém, por favor, crie uma planilha que suporte mais.
Distância média entre números primos
| n | Números primos menores que n | n/(ln(n)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1.000 | 168 | 169 |
| 10.000 | 1.229 | 1.218 |
| 100.000 | 9.592 | 9.512 |
| 1.000.000 | 78.498 | 78.030 |
| 10.000.000 | 664.579 | 661.459 |
| 100.000.000 | 5.761.455 | 5.740.304 |
| 1.000.000.000 | 50.847.534 | 50.701.542 |
| 10.000.000.000 | 455.052.511 | 454.011.971 |
| 100.000.000.000 | 4.118.054.813 | 4.110.416.301 |
| 1.000.000.000.000 | 37.607.912.018 | 37.550.193.650 |
| 10.000.000.000.000 | 346.065.536.839 | 345.618.860.221 |
| 100.000.000.000.000 | 3.204.941.750.802 | 3.201.414.635.781 |
| 1.000.000.000.000.000 | 29.844.570.422.669 | 29.816.233.849.001 |
| 10.000.000.000.000.000 | 279.238.341.033.925 | 279.007.258.230.820 |
| 100.000.000.000.000.000 | 2.623.557.157.654.230 | 2.621.647.966.812.030 |
| 1.000.000.000.000.000.000 | 24.739.954.287.740.800 | 24.723.998.785.920.000 |
| 10.000.000.000.000.000.000 | 234.057.667.276.344.000 | 233.922.961.602.470.000 |
| 100.000.000.000.000.000.000 | 2.220.819.602.560.910.000 | 2.219.671.974.013.730.000 |
| 1.000.000.000.000.000.000.000 | 21.127.269.486.018.700.000 | 21.117.412.262.910.000.000 |
| 10.000.000.000.000.000.000.000 | 201.467.286.689.315.000.000 | 201.381.995.844.660.000.000 |
| 100.000.000.000.000.000.000.000 | 1.925.320.391.606.800.000.000 | 1.924.577.459.166.810.000.000 |
| 1.000.000.000.000.000.000.000.000 | 18.435.599.767.349.200.000.000 | 18.429.088.896.563.900.000.000 |
| 10.000.000.000.000.000.000.000.000 | 176.846.309.399.143.000.000.000 | 176.788.931.049.964.000.000.000 |
Fonte: Quantos números primos existem? em Prime Pages.


