Pergunte ao Mago #353
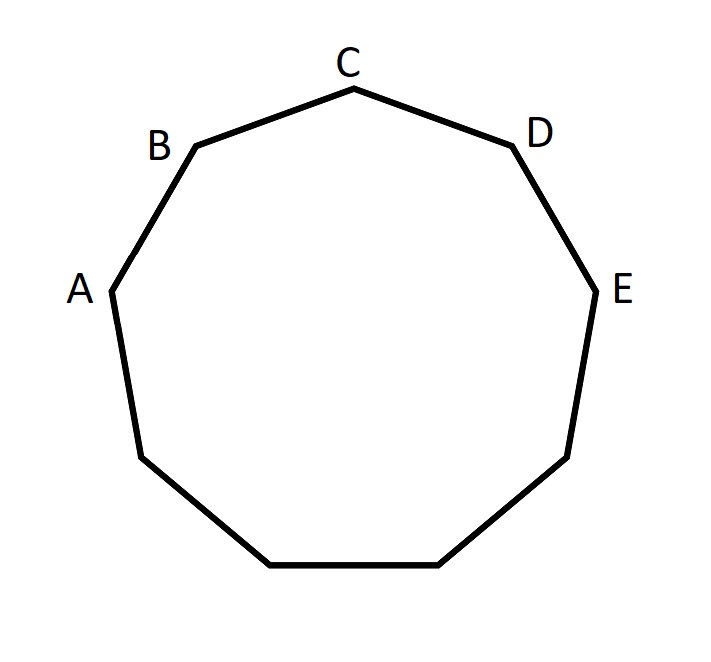
A figura acima é um eneágono com lado de comprimento um.
Qual é maior, AB+AC ou AE?
Este problema foi retirado da edição de março de 2021 do Boletim da Mensa.
Aqui está a minha solução para este problema. (PDF)
Como posso encontrar facilmente a raiz quadrada de qualquer número de três ou quatro dígitos, assumindo que a resposta seja um número inteiro?
A tabela a seguir mostra os números de 0 a 9, o quadrado de cada um deles e o último dígito desse quadrado.
Último dígito de números quadrados
| Original Número | Quadrado | Último dígito da Praça |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
Note que os quadrados dos números pares sempre terminam em 0, 1, 4, 5, 6 ou 9. Isso é válido para todos os quadrados. Isso ocorre porque o último dígito do número original determina o último dígito do quadrado.
Passo 1: Com base no último dígito do quadrado, podemos usar a seguinte tabela para identificar o último dígito da raiz quadrada. Por exemplo, se 2809 for o quadrado, o último dígito da raiz quadrada será 3 ou 7.
Último dígito do número original
| Último dígito da raiz quadrada | Último dígito da Praça |
|---|---|
| 0 | 0 |
| 1 | 1 ou 9 |
| 4 | 2 ou 8 |
| 5 | 5 |
| 6 | 4 ou 6 |
| 9 | 3 ou 7 |
Passo 2: Em seguida, pegue o número original e descarte os dois dígitos da direita. Por exemplo, se o número original fosse 2809, use 28.
Passo 3: Encontre o menor número quadrado menor ou igual ao resultado do passo 2. Em seguida, calcule a raiz quadrada desse número quadrado. Por exemplo, o menor quadrado menor que 28 é 25. Calculando a raiz quadrada de 25, obtemos 5.
Se você não memorizou os quadrados até 100, pode usar a tabela a seguir.
Primeira parte da raiz quadrada
| Passo 2 | Passo 3 |
|---|---|
| 1 a 3 | 1 |
| 4 a 8 | 2 |
| 9 a 15 | 3 |
| 16 a 24 | 4 |
| 25 a 35 | 5 |
| 36 a 48 | 6 |
| 49 a 63 | 7 |
| 64 a 80 | 8 |
| 81 a 99 | 9 |
Passo 4: Se o resultado do passo 1 for 0 ou 5, coloque-o após o resultado do passo 3 e você terminou.
Caso contrário, seja a = resultado da etapa 3. Seja b = a × (a + 1). Por exemplo, se o resultado da etapa 3 for 5, então b = 5 × 6 = 30.
Passo 5: Se b < a, então o último dígito da raiz quadrada é o menor dos valores possíveis obtidos no passo 1. Caso contrário, se b >= a, então é o maior dos dois valores possíveis.
Passo 6: Para obter a raiz quadrada, pegue o resultado do passo 3 e some-o ao resultado do passo 5. Em outras palavras, 10 × (passo 3) + passo 5.
Vejamos alguns exemplos:
Calcule a raiz quadrada de 256.
- Passo 1: O último dígito da raiz quadrada é 4 ou 6.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 2.
- Passo 3: O menor quadrado menor ou igual a 2 é 1. A raiz quadrada de 1 é 1.
- Passo 4: 1*(1+1) = 2.
- Passo 5: O resultado do passo 4 é igual ao do passo 2, então usamos a maior das opções do passo 1 como o último dígito, que é 6.
- Passo 6: A raiz quadrada é o resultado de 3 somado ao resultado do passo 5, que resulta em 1 e 6 = 16.
Calcule a raiz quadrada de 1369.
- Passo 1: O último dígito da raiz quadrada é 3 ou 7.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 13.
- Passo 3: O menor quadrado menor ou igual a 13 é 9. A raiz quadrada de 9 é 3.
- Passo 4: 3*(1+3) = 12.
- Passo 5: O resultado do passo 2 é maior que o do passo 4, então usamos a maior das opções do passo 1 como o último dígito, que é 7.
- Passo 6: A raiz quadrada é o resultado de 3 somado ao resultado do passo 5, que resulta em 3 e 7 = 37.
Calcule a raiz quadrada de 2704.
- Passo 1: O último dígito da raiz quadrada é 2 ou 8.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 27.
- Passo 3: O menor quadrado menor ou igual a 27 é 25. A raiz quadrada de 25 é 5.
- Passo 4: 5*(1+5) = 60.
- Passo 5: O resultado do passo 2 é menor que o do passo 4, então usamos o menor dos valores do passo 1 como o último dígito, que é 2.
- Passo 6: A raiz quadrada é o resultado de 3 somado ao resultado do passo 5, que resulta em 5 e 2 = 52.
Calcule a raiz quadrada de 5625.
- Passo 1: O último dígito da raiz quadrada é 5.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 56.
- Passo 3: O menor quadrado menor ou igual a 56 é 49. A raiz quadrada de 49 é 7.
- Passo 4: O resultado do passo 1 é 0 ou 5, então a resposta é o resultado do passo 3 somado ao do passo 1: 7 e 5 = 75
Calcule a raiz quadrada de 6561.
- Passo 1: O último dígito é 1 ou 9.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 65.
- Passo 3: O menor quadrado menor ou igual a 65 é 64. A raiz quadrada de 64 é 8.
- Passo 4: 8*(1+8) = 72.
- Passo 5: O resultado do passo 2 é menor que o do passo 4, então usamos o menor dos valores do passo 1 como o último dígito, que é 1.
- Passo 6: A raiz quadrada é o resultado de 3 somado ao resultado do passo 5, que dá 8 e 1 = 81.
Você pode ver uma demonstração desse método no YouTube .
Em 12 horas de jogo de blackjack, qual é a probabilidade de se obter 60 ou mais vitórias consecutivas?
De acordo com a minha página sobre variância no blackjack , baseada nas regras liberais do Strip District, as probabilidades de um resultado líquido de vitória, empate ou derrota são as seguintes:
- Vitória — 42,43%
- Empurrão — 8,48%
- Perda — 49,09%
Vamos ignorar os empates, o que nos dá uma probabilidade de vitória, considerando que a mão resultou em um saldo positivo ou negativo, de 46,36%.
Vamos usar 100 mãos por hora como velocidade de jogo.
Podemos aproximar a probabilidade de ver pelo menos uma sequência de pelo menos 60 mãos consecutivas da seguinte forma:
100×12×0,4636 60 = 1 em 89.412.355.233.588.500.Para efeito de comparação, se você comprasse um bilhete da Powerball e um da Mega Millions, a probabilidade de ganhar em ambos seria de 1 em 88.412.922.115.818.300.
Portanto, seria um pouco mais provável ganhar nas duas loterias do que ter 60 vitórias consecutivas em 12 horas de jogo.


