Pergunte ao Mago #355
No filme "Licença para Matar", James Bond joga três rodadas de blackjack, jogando cinco mãos de cada vez. Percebi que ele nunca pediu carta em nenhuma delas. Qual a probabilidade disso?
Você pode encontrar um trecho da cena no YouTube .
O jogo apresenta um número suspeitamente alto de cartas grandes, não é? Aqui estão as cartas que consegui identificar. Observe que, em alguns casos, as cartas não estavam muito nítidas.
Licença para Matar -- Observações sobre as Fileiras
| Classificação | Observado |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| J | 3 |
| P | 6 |
| K | 4 |
| UM | 1 |
| Total | 35 |
Você tem toda razão, Bond não pede carta em nenhuma das suas 15 mãos iniciais. Ele divide um par de oitos uma vez, mas também não pede carta depois de dividir. Aqui está a contagem das suas ações iniciais em todas as 15 mãos:
- Duplo — 1
- Dividir — 1
- Posição — 13
Aqui estão as probabilidades básicas da estratégia para cada ação inicial, considerando seis baralhos, permissão para dobrar após dividir, o dealer espiar a carta fechada e o dealer parar no 17 suave.
Blackjack -- Probabilidades da Primeira Ação
| Ação | Probabilidade |
|---|---|
| Ficar | 43,46% |
| Bater | 39,78% |
| Dobro | 9,53% |
| Dividir | 2,48% |
| Blackjack | 4,75% |
| Total | 100,00% |
Caso a rendição fosse permitida, essa probabilidade seria de 4,14%, em comparação com a probabilidade de permanecer de pé.
Vale ressaltar que Bond já parou em 16 contra 10. A jogada básica da estratégia é pedir carta, mas a margem de sucesso é muito pequena. Dado o grande número de dez que apareceram naquela mão, Bond pode ter percebido que a contagem era alta, o que acionaria uma exceção à estratégia básica, permitindo que ele parasse naquela situação.
A probabilidade de não acertar nenhuma das 15 cartas é de 60,22%. A probabilidade de não acertar 15 das 15 cartas, assumindo que cada carta é independente, é de 0,602162 ÷ 15 = 0,000496253 ≈ 1 em 2015.
Em "O Jogo da Lula", 16 jogadores enfrentam uma ponte de vidro. A ponte é dividida em 18 pares de peças de vidro. Em cada par, uma peça de vidro é temperada e suporta o peso de um jogador. A outra peça do par é de vidro comum e se quebrará sob o peso de um jogador. Se um jogador pisar em uma peça de vidro comum, ela se quebrará e ele cairá, morrendo na queda.
Os jogadores devem avançar, um de cada vez, em uma ordem predeterminada.
Considerando que cada par de degraus de vidro seja atravessado aleatoriamente, qual é o número esperado de jogadores que conseguirão atravessar em segurança?
Vou colocar a resposta e a solução em spoilers, para que todos possam descobrir a resposta por si mesmos.
A probabilidade de o jogador 1 atravessar em segurança é (1/2)^18 = 1/262144 = aproximadamente 0,000004.
Existem duas maneiras pelas quais o jogador 2 pode atravessar com segurança:
- O jogador 1 cruza em segurança. Nesse caso, o jogador 2 pode simplesmente copiar seus passos.
- Entre o jogador 1 e o jogador 2, há apenas um passo ruim. Isso poderia ocorrer em 18 dos 18 pares de copos possíveis. A probabilidade de 17 passos bons e um passo ruim é 18*(1/2)^2 = 18/262144 = 0,000069.
Assim, a probabilidade de o jogador 2 cruzar em segurança é 0,000004 + 0,000069 = 0,000072.
Existem duas maneiras pelas quais o jogador 3 pode atravessar com segurança:
- O jogador 2 cruza em segurança. Nesse caso, o jogador 3 pode simplesmente copiar seus passos.
- Entre os jogadores 1, 2 e 3, existem apenas duas jogadas ruins. Há combin(18,2) = 153 maneiras de escolher 2 dentre os 18 pares de copos para as duas peças que eliminam os jogadores 1 e 2. A probabilidade de 16 jogadas boas e duas jogadas ruins é 153*(1/2)^2 = 153/262144 = 0,000584.
Assim, a probabilidade de o jogador 3 cruzar em segurança é 0,000072 + 0,000584 = 0,000656.
Existem duas maneiras pelas quais o jogador 4 pode atravessar com segurança:
- O jogador 3 cruza em segurança. Nesse caso, o jogador 4 pode simplesmente copiar seus passos.
- Entre os jogadores 1 a 4, há apenas três passos ruins. Existem combin(18,3) = 816 maneiras de escolher 3 dentre os 18 pares de copos para as duas peças que eliminam os jogadores 1 a 3. A probabilidade de 15 passos bons e 3 passos ruins é 816*(1/2)^2 = 816/262144 = 0,003113.
Seguindo essa lógica, obtemos a seguinte tabela com a probabilidade de cada jogador.
Jogo de Ponte
| Jogador | Probabilidade Sobrevivência |
|---|---|
| 1 | 0,000004 |
| 2 | 0,000072 |
| 3 | 0,000656 |
| 4 | 0,003769 |
| 5 | 0,015442 |
| 6 | 0,048126 |
| 7 | 0,118942 |
| 8 | 0,240341 |
| 9 | 0,407265 |
| 10 | 0,592735 |
| 11 | 0,759659 |
| 12 | 0,881058 |
| 13 | 0,951874 |
| 14 | 0,984558 |
| 15 | 0,996231 |
| 16 | 0,999344 |
| Total | 7,000076 |
Para expressar a resposta em forma fechada, temos:
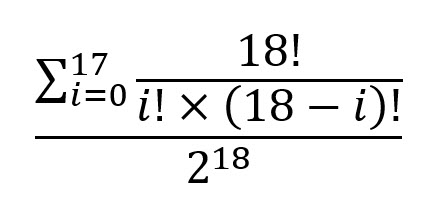
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Na sua partida Ultimate X Gold , aos 3:10, você recebeu um full house, com três cartas iguais sobre quatros. Seu multiplicador para qualquer quadra de 2 a 4 era 9x. O multiplicador para um full house era 1x. Por que você manteve o full house, em vez de apenas tentar a quadra com o multiplicador maior?
Você tem razão, eu estraguei tudo com aquela mão.
Lembre-se que eu estava jogando 10 partidas. Portanto, meu ganho com a casa cheia foi de 10 × 35 = 350.
Ao segurar apenas os três, cada mão tinha as seguintes probabilidades:
- Quadra — 4,26%
- Casa cheia — 6,11%
- Três iguais — 89,64%
Aqui estão os ganhos de cada mão, após os multiplicadores:
- Quatro de um tipo — 1800
- Casa cheia — 35
- Três de um tipo — 15
Meu retorno esperado, tendo apenas os três, teria sido (4,26% * 1800) + (6,11% * 35) + (89,64% * 15) = 92,17854. Isso é significativamente maior do que os 35 do full house. Então, sim, cometi um erro vergonhoso com essa mão.
Alguém me desafiou para a seguinte aposta. Eu posso escolher três cartas de um baralho de pôquer padrão, anotando meu palpite, mas mantendo-o em segredo até o final. Por exemplo, 7-Ás-2. Ele então me ofereceu uma aposta de valor igual que conseguiria acertar pelo menos uma das minhas cartas se recebesse três palpites. Quais eram as minhas chances de ganhar?
Para ganhar, seu oponente precisa errar todas as três previsões. A primeira previsão tem 10/13 de chance de estar errada. A segunda previsão tem 9/12 de chance de estar errada, porque podemos descartar a primeira classificação como possibilidade. A terceira previsão tem 8/11 de chance de estar errada, porque podemos descartar as duas primeiras classificações como possibilidade.
Todas as três coisas teriam que acontecer para você ganhar. Assim, as chances de você ganhar são (10/13) * (9/12) * (8/11) = 720/1716 = 41,96%.
Com odds de 1 para 1, a vantagem da casa nessa aposta, do seu lado, é de 16,08% (ai!).
Esta pergunta foi extraída do livro The Book of Proposition Bets, de Owen E'Shea (número 7).


