Pergunte ao Mago #367
Eu gosto de apostar em todos os números no craps. Quantos números diferentes posso esperar acertar antes de tirar um 7?
Para benefício dos demais leitores, a pergunta é: quantas das seguintes totais serão obtidas ao rolar dois dados antes de se obter um total de sete?
A resposta é 2,375758. A tabela a seguir mostra a probabilidade de cada possibilidade individual de rolar de zero a seis totais únicos no intervalo especificado. A célula inferior direita mostra a média dos totais únicos rolados antes de um sete.
Números únicos sorteados
| Total | Probabilidade | Esperado |
|---|---|---|
| 6 | 0,062168 | 0,373009 |
| 5 | 0,101016 | 0,505079 |
| 4 | 0,129245 | 0,516979 |
| 3 | 0,151531 | 0,454594 |
| 2 | 0,170057 | 0,340114 |
| 1 | 0,185983 | 0,185983 |
| 0 | 0,200000 | 0,000000 |
| Total | 1.000000 | 2,375758 |
É verdade que, ao lançar uma moeda honesta, é mais provável que a face que estava inicialmente voltada para cima fique voltada para cima?
As evidências sugerem que isso é verdade!
Persi Diaconis e Susan Holmes, da Universidade de Stanford, registraram 10.000 lançamentos de moeda. A moeda caiu com a face para cima na mesma posição inicial em 50,8% das vezes (fonte: The Fifty-one Percent Solution, do boletim informativo What's Happening in the Mathematical Sciences, da American Mathematical Society). A probabilidade de uma proporção tão alta ou maior é de 5,48%.
Para provar isso matematicamente, assumi que o número real de rotações de uma moeda seguia a distribuição de Poisson. Mais especificamente, se o número médio de rotações fosse m, então a probabilidade de ocorrerem exatamente n rotações seria exp(-m)*m^n/n!. Para ilustrar a distribuição de Poisson, o gráfico a seguir mostra a probabilidade de ocorrerem de 0 a 25 rotações, dada uma média de 10.
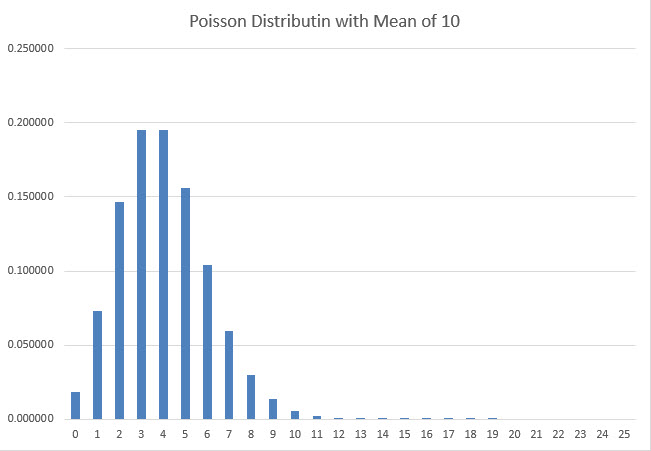
A razão pela qual escolhi a hipótese de Poisson é que ela segue uma forma próxima à de uma curva em forma de sino para médias suficientemente grandes, e o resultado real nunca pode ser inferior a zero.
Em seguida, calculei a probabilidade de um número par de meias-revoluções (resultando no mesmo lado da face inicial para cima) para várias médias de meias-revoluções. A tabela a seguir mostra os resultados para médias de 0,5 a 5,0.
Probabilidade de um número par ou ímpar de revoluções
| Revoluções Médias | Total par | Total Ímpar |
|---|---|---|
| 0,5 | 0,567667642 | 0,432332358 |
| 1 | 0,509157819 | 0,490842181 |
| 1,5 | 0,501239376 | 0,498760624 |
| 2 | 0,500167731 | 0,499832269 |
| 2,5 | 0,500022700 | 0,499977300 |
| 3 | 0,500003072 | 0,499996928 |
| 3,5 | 0,500000416 | 0,499999584 |
| 4 | 0,500000056 | 0,499999944 |
| 4.5 | 0,500000008 | 0,499999992 |
| 5 | 0,500000001 | 0,499999999 |
Então, comecei a me perguntar por que a probabilidade de um número par era sempre maior que 50%. Acontece que a probabilidade de um número par, dada uma média de m, pode ser expressa como 0,5 + e^(-2m)/2. Como e elevado a qualquer potência deve ser positivo, a probabilidade de um número par de revoluções também é positiva.
Você pode ver a minha demonstração desta fórmula aqui .
Qual a sua análise do jogo Spelling Bee no programa The Price is Right?
Para benefício dos demais leitores, permitam-me repassar as regras primeiro.
- Existe um tabuleiro com 30 cartas, numeradas de 1 a 30.
- No verso de cada cartão há uma letra ou a palavra "carro". A distribuição de cada uma é a seguinte:
- C: 11
- A: 11
- R: 6
- Carro: 2
- Os anfitriões permitem que o jogador escolha duas cartas.
- Após um jogo de precificação, no qual não entrarei em detalhes, o jogador tem a oportunidade de ganhar até três cartas adicionais.
- As cartas serão viradas.
- O jogador pode ganhar um carro de duas maneiras:
- O jogador recebe pelo menos uma carta de cada letra (formando assim a palavra CARRO).
- O jogador recebe pelo menos uma das cartas "CARRO".
- A qualquer momento do jogo, o jogador pode desistir e receber $1.000 por cada uma de suas cartas que ainda não tiver virado.
Aqui está um vídeo do jogo sendo disputado.
A tabela a seguir mostra a probabilidade de ganhar, de acordo com a quantidade de cartas que o jogador possui, supondo que nenhuma tenha sido virada ainda.
Concurso de Soletração — Probabilidade de Vitória
| Cartões | Probabilidade Vencendo |
|---|---|
| 2 | 0,131034 |
| 3 | 0,371921 |
| 4 | 0,584018 |
| 5 | 0,734888 |
Antes de qualquer carta ser virada, o jogador não deve desistir, assumindo qualquer valor razoável para o carro. Por exemplo, mesmo com apenas duas cartas, o jogador tem 13,1% de chance de ter pelo menos uma das cartas CARRO. O jogador deve ser indiferente a um valor de desistência de $2.000 se o carro tiver um valor de $15.263,16. Qualquer carro novo valerá mais do que isso.
A seguir, são apresentados os pontos de indiferença no valor do carro, de acordo com a quantidade de cartas não viradas que o jogador possui.
Concurso de Soletração — Probabilidade de Vitória
| Cartões | Indiferença Apontar |
|---|---|
| 2 | $ 15.263,16 |
| 3 | $ 8.066,23 |
| 4 | $ 6.849,11 |
| 5 | $ 6.803,75 |


