Pergunte ao Mago #372
Vi que o prêmio acumulado do Face Up Pai Gow Poker Mega nos cassinos Caesars em Las Vegas está acima de US$ 3,9 milhões. Vale a pena apostar nisso atualmente?
Consultei vários sites da Caesars no dia 1 de outubro e encontrei esta tabela de pagamentos para a aposta progressiva de $5 no Face Up Pai Gow Poker.
- Sequência de sete cartas = $ 3.922.620
- Cinco ases = $185.104
- Royal Flush = $ 2.969
- Straight flush = $500
- Quadra = $375
- Casa cheia = $20
Analiso essa aposta na minha página sobre Face Up Pai Gow Poker . Nesse caso, o Mega Jackpot, para um straight flush de sete cartas, está excepcionalmente alto. Acredito que normalmente fique na faixa dos cinco dígitos baixos. Resumindo, essa aposta de $5 tem um retorno esperado de $9,55! Isso significa um lucro esperado de $4,55.
Você ainda precisa fazer uma aposta negativa no jogo base. O valor mínimo varia de US$ 15 a US$ 100. Com uma vantagem da casa de 1,81%, aqui está a perda esperada por valor apostado no jogo base.
- Aposta de $15 = prejuízo de $0,27
- Aposta de $25 = prejuízo de $0,45
- Aposta de $50 = prejuízo de $0,90
- Aposta de $100 = prejuízo de $1,81
Com uma aposta base de $251,61 e $5 no jackpot progressivo, o jogo combinado teria vantagem da casa zero.
No entanto, dois grandes motivos para não apostar nisso são a alíquota máxima do imposto de renda federal, de 37%, e a enorme volatilidade. O jogador médio que não acerta nenhuma das três combinações progressivas principais pode esperar perder US$ 3,38 por mão com uma aposta base de US$ 15 e US$ 3,56 com uma aposta de US$ 25. Isso se acumula a cada hora.
Ainda assim, matematicamente, é uma aposta muito positiva. Com uma aposta base de US$ 15, a vantagem combinada dos jogadores é de 21,39%. Isso não se vê todos os dias.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Ouvi dizer que os hotéis da MGM em Las Vegas agora cobram a comissão da casa apenas nas apostas de compra após uma vitória. Como isso altera a vantagem da casa?
Acredito que a taxa da casa já é cobrada após uma vitória apenas nos números 4 e 10. Portanto, não há diferença nesse aspecto. Aqui está a vantagem da casa nos números 4 e 10, considerando as três formas de apostar:
- Aposta de lugar (paga 9 para 5) — 6,67%
- Aposta de compra (comissão sempre paga) — 4,76%
- Aposta de compra (comissão paga apenas sobre os ganhos) — 1,76%
Nos números 5 e 9, isso é uma boa notícia, reduzindo a vantagem da casa de 4,00% em uma aposta de lugar para 2,00%.
- Aposta de colocação (paga 7 para 5) — 4,00%
- Aposta de compra (comissão sempre paga) — 4,76%
- Aposta de compra (comissão paga apenas sobre os ganhos) — 2,00%
Nos números 6 e 8, não importa, pois a vantagem da casa nas apostas de lugar ainda é menor.
- Aposta de lugar (paga 7 para 6) — 1,52%
- Aposta de compra (comissão sempre paga) — 4,76%
- Aposta de compra (comissão paga apenas sobre os ganhos) — 2,27%
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
No episódio 4 da 37ª temporada de Survivor, houve um desafio em que quatro peças de quebra-cabeça podiam ser organizadas tanto em um quadrado quanto em um triângulo equilátero. Quais seriam as dimensões exatas das peças para que isso funcionasse?
 |  |
Primeiro, vamos fazer um diagrama adequado e rotulá-lo.
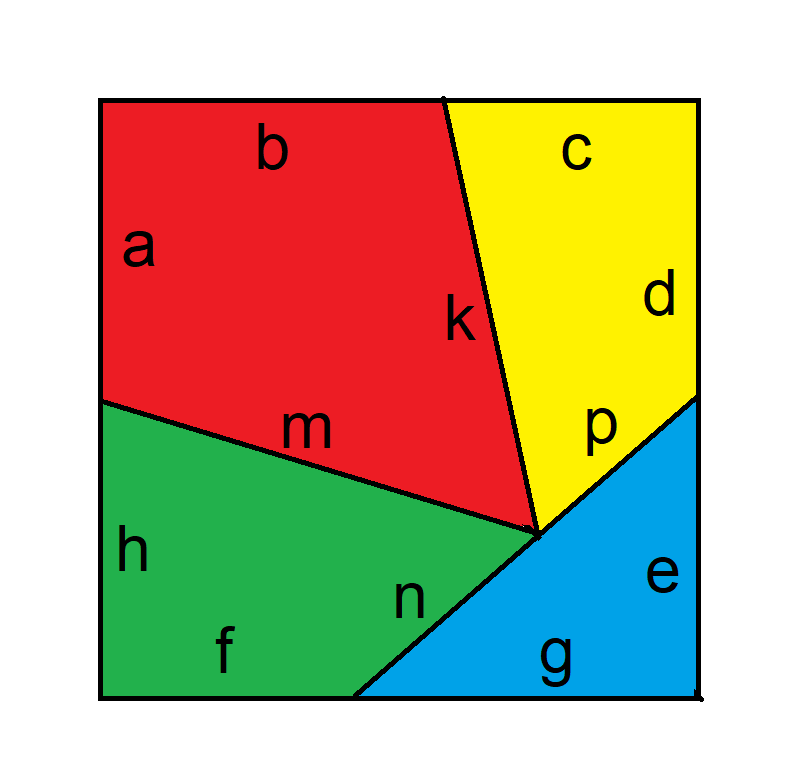
A seguir, apresentamos o diagrama do triângulo resolvido.
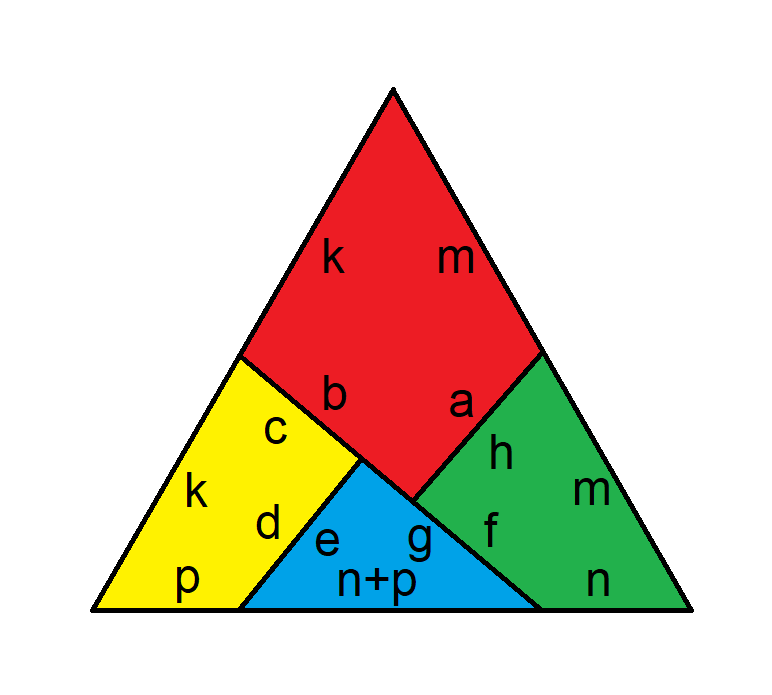
Em seguida, supondo que os lados do quadrado tenham comprimento 1, aqui está o comprimento de cada letra no diagrama acima.
a = d = e = h = 1/2
b = g = QUADRADO((4-QUADRADO(3))/(4*QUADRADO(3))) =~ 0,572145321740575
c = f = 1-QUADRADO((4-QUADRADO(3))/(4*QUADRADO(3))) =~ 0,427854678259425
k = m = 1/SQRT(SQRT(3)) =~ 0,759835685651592
n = (3-QUADRADO(4*QUADRADO(3)-3))/(2*QUADRADO(QUADRADO(3))) =~ 0,386767938902275
p = (QUADRADO(4*QUADRADO(3)-3)-1)/(2*QUADRADO(3))) =~ 0,373067746749317
Finalmente, aqui está minha solução completa (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .



