Pergunte ao Mago #373
Tenho certeza de que você é fã de The Big Bang Theory. Uma das minhas cenas favoritas é a do jogo de Pedra, Papel e Tesoura com o Spock Lagarto. É como um jogo de Pedra, Papel e Tesoura com cinco símbolos, com as seguintes regras:
- Papel cobre rocha
- Pedra esmaga lagarto
- Lagarto envenena Spock
- Spock esmaga tesouras
- Tesoura corta papel
- Lagarto come papel Spock vaporiza rocha
- Tesoura decapita lagarto
- Artigo refuta Spock
- Pedra esmaga tesouras
Minha pergunta é: é possível adicionar mais símbolos, de forma que todos os lados tenham as mesmas chances contra um jogador aleatório?
Sim, eu também adoro essa cena! Aqui está um vídeo dela no YouTube .
Você precisa de um número ímpar de símbolos. Em teoria, você poderia ter um número par, mas aí teria que criar regras em que certos pares de símbolos diferentes resultassem em empate. Não, queremos um jogo decisivo em que os únicos empates ocorram se ambos os jogadores jogarem o mesmo símbolo.
Uma solução é especialmente elegante e fácil de explicar com um número primo de símbolos. Permita-me explicar com sete símbolos, como exemplo. Vamos rotular os símbolos de A a G e representá-los em um círculo, no diagrama a seguir.
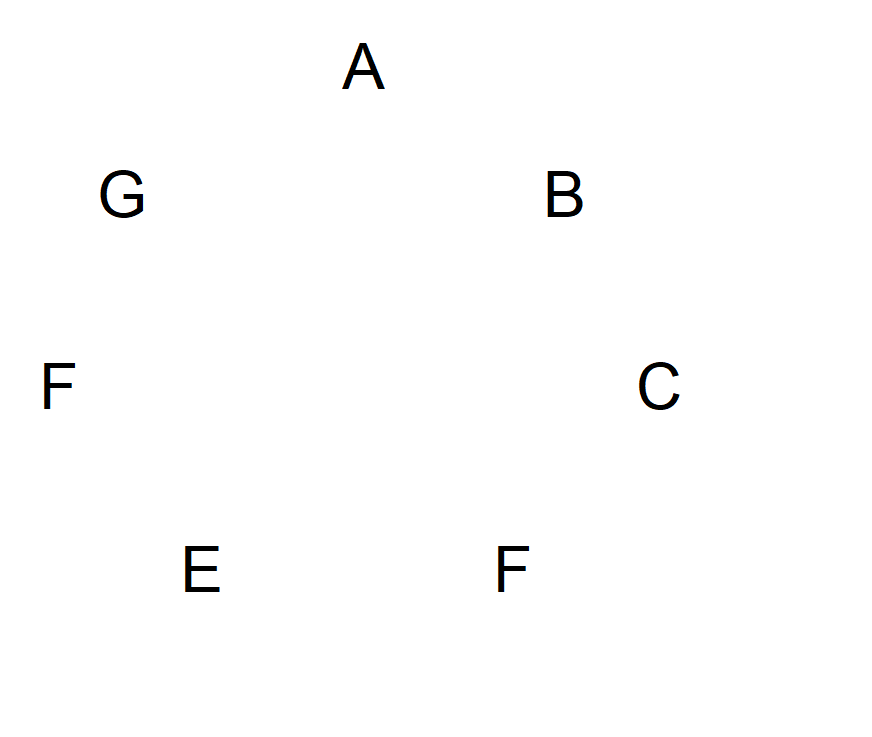
Em seguida, comece com A e desenhe uma seta para o próximo símbolo no sentido horário. A seta deve apontar para o símbolo que está entre esses dois. Imagine que esse símbolo está sendo atingido por uma flecha. Continue no sentido horário até retornar a A. O diagrama não ficará assim:
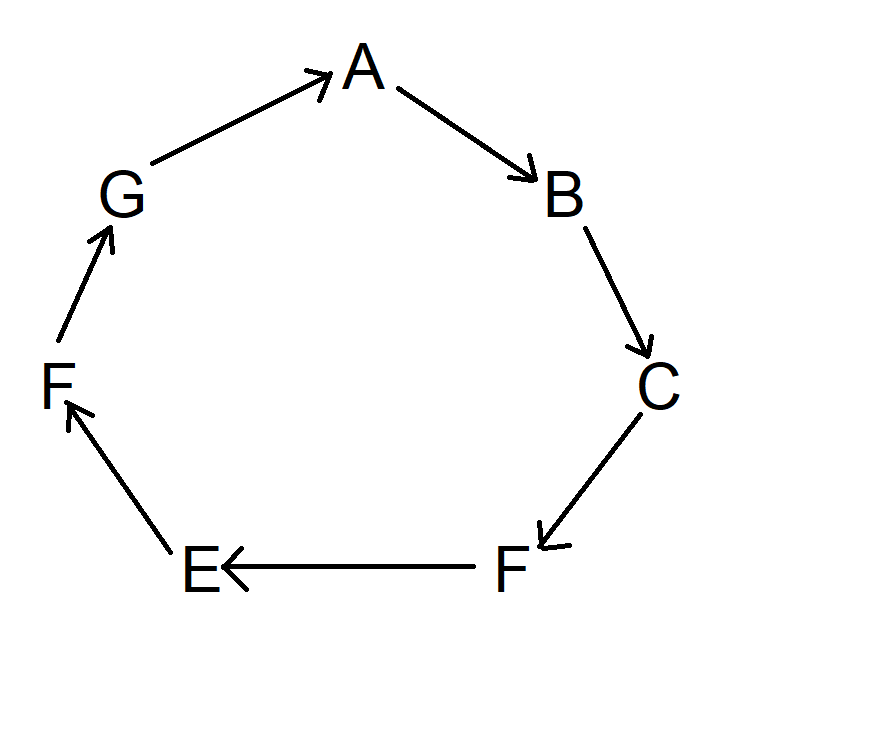
Em seguida, faça o mesmo, mas avance dois símbolos no sentido horário, começando em A. Na verdade, você pode começar em qualquer lugar que desejar. O diagrama agora se parece com isto:
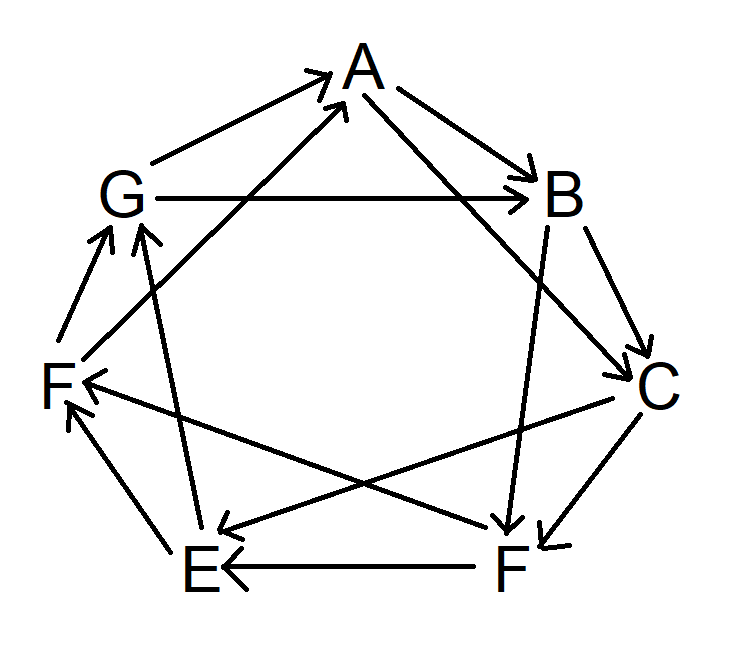
Por fim, faça o mesmo, mas pule três símbolos no sentido horário. O diagrama agora ficará assim:
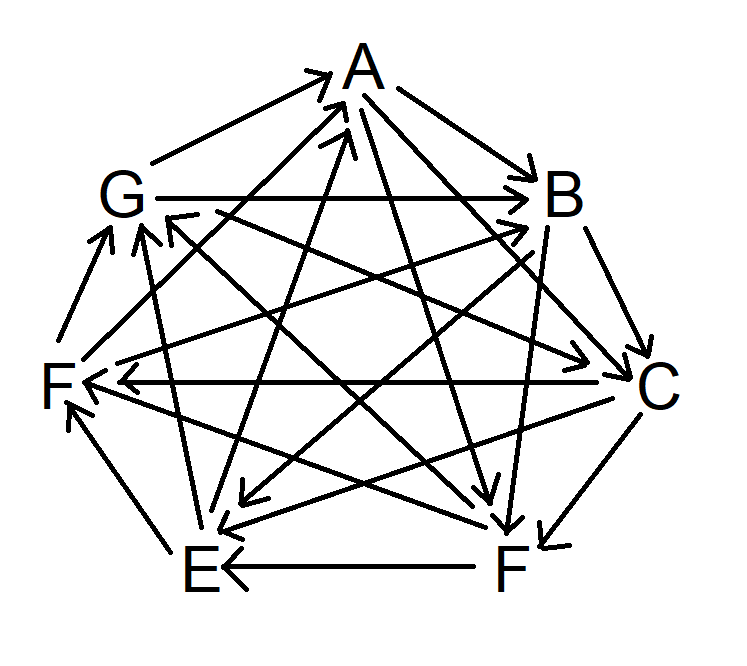
Observe que, neste ponto, cada símbolo vence outros três símbolos e é vencido por outros três símbolos diferentes.
Este método funciona para qualquer número primo de símbolos, pois, ao retornar ao símbolo original, você já terá passado por todos os símbolos. Para n símbolos, você terá que repetir esse processo (n-1)/2 vezes.
É possível criar um jogo equilibrado com qualquer número ímpar de símbolos, mas, às vezes, você retornará ao símbolo original muito rapidamente. Quando isso acontecer, você terá que fazer novos loops começando pelos símbolos que perdeu.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Qual a probabilidade de um empate no Three Card Poker?
A resposta exata é 450528/407170400 =~ 0,001106485 =~ 1/904.
A tabela a seguir mostra o número de maneiras de formar cada tipo de mão inicial e o número de combinações que empatam na segunda mão. No caso de sequências e mãos descartáveis, é importante saber se há dois ou três naipes representados na primeira mão.
A célula inferior direita mostra que existem 450.528 maneiras de empatar no Three Card Poker. O número total de combinações para duas mãos é combin(52,3)*combin(49,3) = 407170400. Portanto, a resposta é 450528/407170400.
Empate no Three Card Poker
| Mão | Mão 1 | Mão 2 | Produto |
|---|---|---|---|
| Três de um tipo | 52 | 0 | 0 |
| Straight flush | 48 | 3 | 144 |
| Sequência (três naipes) | 288 | 26 | 7.488 |
| Direto (dois ternos) | 432 | 25 | 10.800 |
| Descarga | 1.096 | 3 | 3.288 |
| Par | 3.744 | 3 | 11.232 |
| Lixo (três ternos) | 6.576 | 26 | 170.976 |
| Lixo (dois ternos) | 9.864 | 25 | 246.600 |
| Total | 22.100 | 450.528 |
Qual o valor de um cupom de ás grátis no blackjack 6-5?
Na minha página sobre o valor de um ás grátis , afirmo que seu valor é de 50,1844% do valor da aposta no blackjack 3-2.
No blackjack com seis baralhos, a probabilidade de obter um blackjack vencedor, com um ás como primeira carta, é de 29,3139%. Quando isso acontece, você ganha 0,3 unidades a menos no blackjack 6-5 do que no 3-2.
Assim, o valor de um ás grátis no blackjack 6-5 com seis baralhos é 50,1844% × 29,3139 × 0,3 = 41,3902% da aposta inicial.
Alguém me desafiou para uma aposta: ele conseguiria tirar um total de 12 com dois dados em 27 lançamentos. Se não conseguisse, eu ganharia o dobro do valor apostado. Como a probabilidade de tirar 12 é de 1/36, não deveria ele precisar de 36 lançamentos em média para conseguir um 12? Parece que as probabilidades estariam a meu favor se meu oponente fizesse apenas 27 lançamentos. Estou certo ou onde está o erro nos meus cálculos?
O tempo médio de espera entre um 12 e outro é de 36 lançamentos, incluindo o próprio lançamento do 12. No entanto, isso não significa que eles aparecem exatamente a cada 36 lançamentos. A probabilidade de NÃO tirar um 12 é (35/36). A probabilidade de não tirar um 12 em 27 lançamentos é (35/36)^27. Portanto, a probabilidade de tirar pelo menos um 12 é 1 - (35/36)^27 = 53,26%.
A tabela a seguir mostra a probabilidade de obter pelo menos 12 em 20 a 36 lançamentos. Observe que são necessários 25 lançamentos para ter vantagem com probabilidades iguais.
Probabilidade 12
| Rolls | Probabilidade |
|---|---|
| 20 | 43,07% |
| 21 | 44,66% |
| 22 | 46,19% |
| 23 | 47,69% |
| 24 | 49,14% |
| 25 | 50,55% |
| 26 | 51,93% |
| 27 | 53,26% |
| 28 | 54,56% |
| 29 | 55,82% |
| 30 | 57,05% |
| 31 | 58,24% |
| 32 | 59,40% |
| 33 | 60,53% |
| 34 | 61,63% |
| 35 | 62,69% |
| 36 | 63,73% |


