WOO logo

Recomendações do Mago

Pergunte ao Mago #375

A Consumer Reports argumenta que o consumidor economizará dinheiro com pneus se fizer o rodízio. O argumento é que, em um carro com tração dianteira, que é o caso da maioria, um pneu dura cerca de 32.000 quilômetros e os pneus traseiros, cerca de 96.000 quilômetros. Eles afirmam que, se os pneus forem rodiziados com frequência, a vida útil deles aumenta para cerca de 64.000 quilômetros.

Dito isso, se um motorista não fizer o rodízio dos pneus, em 120.000 milhas ele pode esperar gastar seis pares de pneus dianteiros e dois pares de pneus traseiros, totalizando 2×(2+6)=16 pneus. Enquanto isso, se outro motorista fizer o rodízio dos pneus, ele gastará três jogos de quatro pneus, totalizando 12 pneus.

Tem algo de estranho aqui. O atrito total dos pneus por quilômetro não é o mesmo, independentemente de serem rotacionados ou não? Não nego os benefícios de segurança da rotação dos pneus, mas por que os pneus magicamente se desgastariam mais lentamente se fossem rotacionados?

anônimo

Boa pergunta. Concordo com seus cálculos, baseados nas premissas fornecidas pela Consumer Reports. No entanto, discordo das premissas deles. Parece que foram preguiçosos e usaram a média da vida útil dos pneus dianteiros e traseiros para calcular a vida útil de um pneu rotacionado.

Para ilustrar, considere um motorista que começa com quatro pneus novos. Ele então troca os pneus dianteiros e traseiros após 15.000 milhas (aproximadamente 24.000 km). Antes da troca, os pneus dianteiros teriam se desgastado 75% e os traseiros 25%. Após a troca, os pneus dianteiros terão 75% da banda de rodagem restante e os traseiros 25%. Ele então dirige mais 15.000 milhas (aproximadamente 24.000 km). Novamente, os pneus dianteiros se desgastarão 75% em relação a um pneu novo e os traseiros 25%. Isso fará com que ambos fiquem com a banda de rodagem zerada após 30.000 milhas (aproximadamente 48.000 km). Não 40.000 milhas (aproximadamente 64.000 km), como afirma a Consumer Reports.

Para obter a vida útil correta com o rodízio de pneus, deve-se calcular a média do desgaste da banda de rodagem. Neste caso, calculamos a média de 1/20.000 e 1/60.000 para obter 1/30.000. Em seguida, calculamos o inverso dessa média de desgaste por quilômetro para obter a vida útil dos pneus após o rodízio, que é de 30.000. Ou você pode usar a fórmula 2*F*R/(F+R), onde F = vida útil do pneu dianteiro e R = vida útil do pneu traseiro.

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .

Sabemos que existem combin(52,5) = 2.598.960 combinações possíveis de cinco cartas dentre 52. Minha pergunta é: quantas mãos de cinco cartas são possíveis com um sapato de cinco baralhos?

anônimo

Vamos analisar um tipo de mão de cada vez.

  • Cinco cartas iguais: Um baralho contém 52 cartas diferentes, resultando em 52 combinações.
  • Quatro cartas iguais: Existem 52 combinações possíveis de quatro cartas iguais e 51 combinações possíveis de uma carta única. Portanto, existem 52 * 51 = 2.652 combinações possíveis para uma quadra.
  • Três cartas iguais e duas cartas diferentes: Existem 52 combinações possíveis para as três cartas iguais e 51 para o par. Portanto, existem 52 * 51 = 2.652 combinações possíveis para um full house.
  • Três cartas iguais e duas cartas diferentes: Existem 52 combinações possíveis para as três cartas iguais e combin(51,2)=1.275 para as duas cartas diferentes. Portanto, existem 52 * 1.275 = 66.300 combinações possíveis para uma trinca.
  • Dois pares de cartas iguais e uma carta avulsa: Existem combin(52,2) = 1.326 combinações para as duas cartas diferentes que formam pares. Restam então 50 combinações para a carta avulsa. Portanto, existem 1.326 * 50 = 66.300 combinações possíveis para um par de duas cartas.
  • Um par de cartas iguais e três cartas avulsas: Existem 52 cartas possíveis para o par. Então, existem combin(51,3) = 20.825 maneiras de escolher 3 cartas dentre as 51 restantes para as cartas avulsas. Portanto, o número de combinações para um par é 52 * 20.825 = 1.082.900.
  • Cinco singletons: Existem combin(52,5)=2.598.960 maneiras de escolher cinco cartas dentre 52.

A soma de todas essas combinações é 3.819.816.

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .

Considere o seguinte diagrama com um quadrado e um círculo?

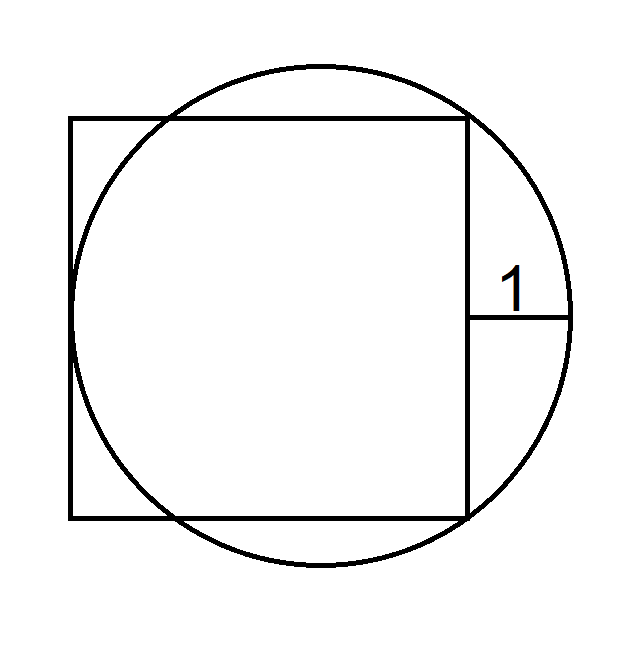
Faça a pergunta 375 ao mago

Qual é a área do quadrado?

anônimo

16

Para minha solução, considere o seguinte diagrama.

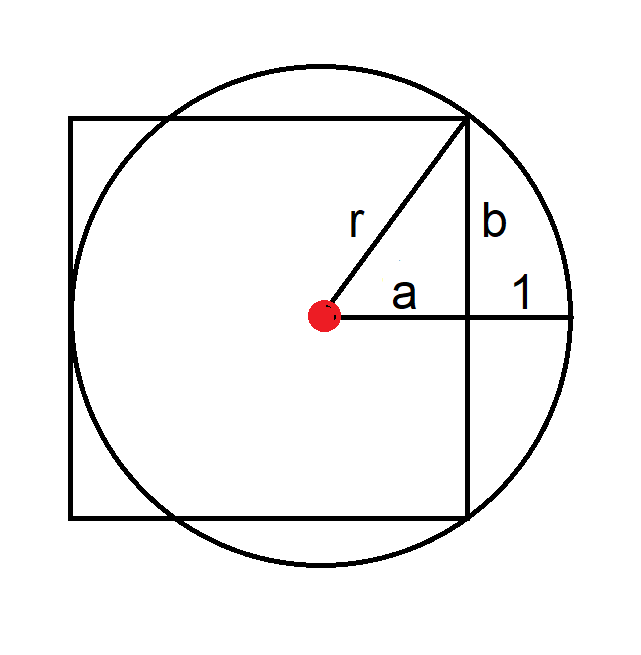
pergunte ao mago 375 solução

Aqui está minha solução (PDF).

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .