WOO logo

Recomendações do Mago

Pergunte ao Mago #377

Suponha que três empresas fabriquem widgets com diferentes graus de defeitos. Em particular, aqui estão as taxas de ocorrência de um widget sem defeitos, considerando as três empresas:

  • Acme: 85%
  • Castanho: 90%
  • Charme: 95%

Existem também três lojas que vendem widgets: Delta, Theta e Omega. Há uma relação direta entre lojas e fabricantes, mas você não sabe qual é essa relação.

Você realiza uma amostragem aleatória das três lojas, com os seguintes resultados:

Dados de teste

Loja Eficaz Defeituoso
Delta 10 0
Teta 48 2
Ómega 186 14

Seu objetivo é comprar um produto eficiente. De qual loja você deve comprar? Qual a probabilidade de sucesso em cada loja?

anônimo

Você deve comprar na loja B. Aqui está a probabilidade de obter um produto em bom estado em cada loja:

  • Delta: 91,76%
  • Theta: 93,57%
  • Ômega: 92,91%
Qual a sua opinião sobre a mão de pôquer entre Robbi Jade e Garrett Adelstein? Robbi trapaceou?

anônimo

Este assunto já foi exaustivamente analisado online, mas não vejo muitas pessoas concordando comigo, então vou dar meu pitaco.

Estou do lado de Robbi Jade.

Para resumir a história, os dois estavam em um jogo de pôquer televisionado com outros grandes nomes do pôquer, incluindo Phil Ivey. Deixe-me dar um resumo rápido. Ambos tinham mãos ruins. Garrett Adelstein fez uma aposta alta e Robbi Jade pagou. Pôquer não é meu forte quando se trata de jogos de azar, mas até eu entendo que com uma mão fraca você geralmente aposta agressivamente ou desiste. Você não paga. É o básico do pôquer.

Para resumir a história, Robbi jogou a mão de uma forma não convencional e venceu. Como mencionado, era um torneio televisionado, com leitores de cartas. Após a vitória, Garrett acusou Robbi de trapaça. Presumo que seu argumento fosse que ela estava em conluio com alguém na transmissão e que recebia sinais das cartas do oponente.

Robbi explicou no programa que cometeu um erro, pensando que suas cartas fechadas eram J/3, em vez do J/4 que ela realmente tinha. Um três, pelo menos, formava um par na mesa.

Mais tarde, nos bastidores do jogo, ela devolveu a Garrett os 135 mil dólares que ele havia perdido na rodada. Ela disse que o motivo era que não queria nenhum drama ou ressentimento entre eles.

Ainda não entendo por que ela devolveu o dinheiro. Os teóricos da conspiração dizem que foi uma admissão de culpa por ter traído. No entanto, não acho que muitos traidores se sintam culpados depois do ocorrido e devolvam o dinheiro. Acho mais comum que pessoas honestas abram mão do dinheiro que ganharam honestamente, apenas para evitar conflitos e manter uma imagem ilibada.

Há mais detalhes na história que não vou mencionar. Resumindo, Garret foi derrotado de forma justa e limpa naquela mão. Em qualquer jogo que combine sorte e habilidade, às vezes o jogador mais fraco vence. Qualquer jogador de pôquer já viu isso milhares de vezes.

Aqui está um trecho do jogo.

Momentos relevantes:

  • 2:07:24 a 2:24:16 -- Entregar a pergunta
  • 2:54:00 a 2:56:00 -- Drama fora das câmeras, no qual outro jogador descobre que Robbi devolveu os US$ 135.000 para Garrett. Outro jogador, com quem concordo, chama Garrett de "covarde".
  • 3:11:25 a 3:20:52 -- Discussão à mesa sobre Robbi pagar US$ 135.000 a Garret.
  • 3:37:59 a 3:43:14 -- Robbi comenta sobre a mão

Todas as figuras na imagem a seguir são quadrados. O comprimento dos lados do quadrado azul é desconhecido. Qual é a área do triângulo ABC?

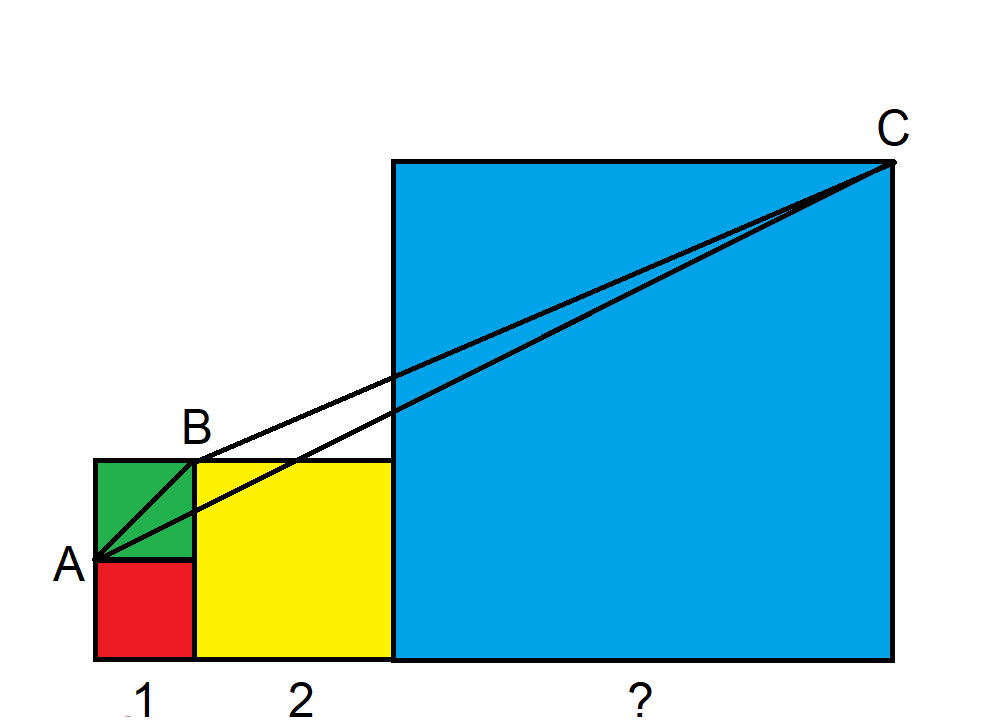
pergunte ao mago 377

anônimo

A resposta é 2.

Considere o seguinte diagrama.

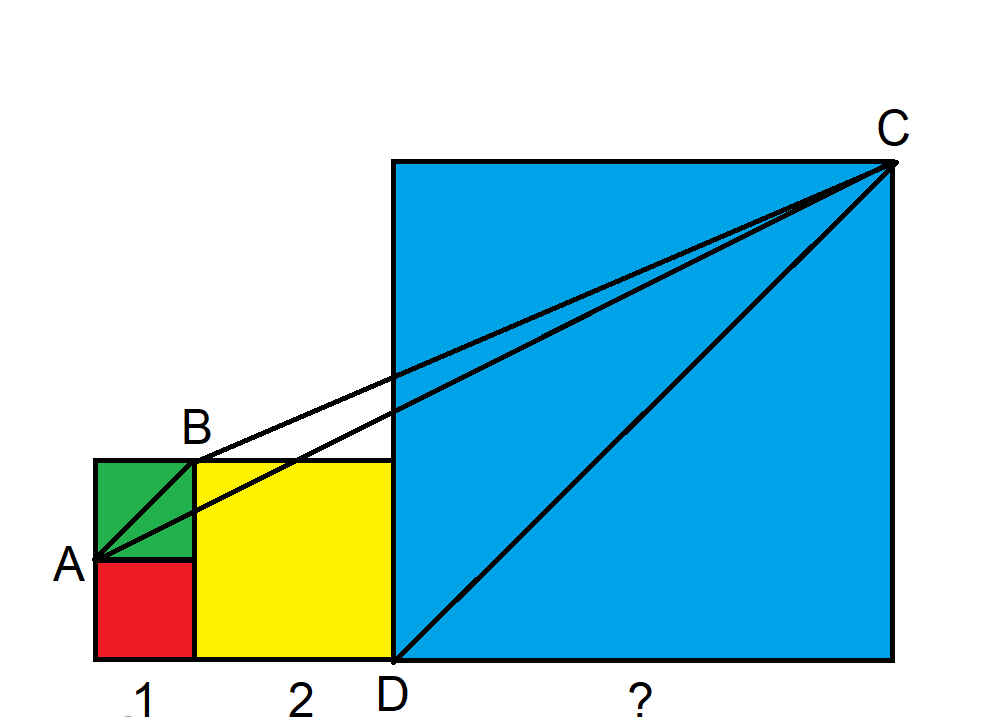
atw 377 s

Observe que as retas AB e CD formam ângulos de 45 graus. Portanto, elas são paralelas.

Lembre-se de que a área de um triângulo é (1/2) × base × altura. Portanto, o tamanho do quadrado azul não importa. A altura do triângulo ABC será sempre a mesma. A área é a mesma do triângulo ABD, porque D tem a mesma altura que qualquer C.

A geometria simples mostra que AB = sqrt(2) e BD = 2*sqrt(2). Assim, a área de ABC = ABD = (1/2) * sqrt(2) * (2*sqrt(2)) = 2.