Pergunte ao Mago #379

A tabela a seguir mostra minha segunda palavra recomendada, de acordo com seu desempenho após jogar STARE. Listei todas as situações em que a soma de amarelos e verdes é de 0 a 2. Em duas situações, não encontrei nenhuma palavra válida.

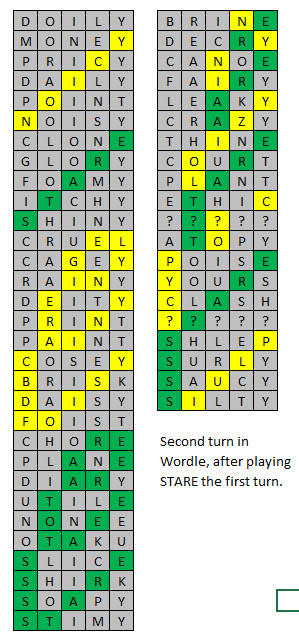
Por exemplo, se STARE resultar apenas em um amarelo na quinta posição (da esquerda), jogue MONEY como sua segunda jogada.

Minha recomendação se baseia principalmente na palavra que tem as letras mais usadas, especialmente nessas posições. No entanto, também levei em consideração algumas palavras que ouvi por aí. Para ver uma lista das minhas dez principais palavras para cada situação, consulte meu post sobre o assunto no Wizard of Vegas .

Para quem não conhece, o Doey Don't funciona da seguinte maneira:

1. Em uma rodada inicial (come-out roll), faça uma aposta de passe (pass) e uma aposta de não passe (don't pass), ambas com o mesmo valor.
2. Se um ponto for sorteado, aposte nas probabilidades.

A ideia é que a aposta "don't pass" seja uma proteção contra um 7 na rodada inicial. Jogadores que apostam no "doey don't" provavelmente diriam que o "pass" e o "don't" se anulam, permitindo que o jogador aproveite a aposta nas probabilidades sem vantagem para a casa.

A falha ocorre se um 12 for rolado na jogada inicial. A aposta de passe perde e a aposta de não passar resulta em empate, causando uma perda de uma unidade. A probabilidade de sair um 12 é de 1/36, o que torna a perda esperada com essa estratégia de 1/36 = 2,78% de uma unidade. Enquanto isso, a perda esperada ao fazer apenas uma aposta de passe e aceitar as probabilidades é de 7/495 = 1,41% de uma unidade.

No entanto, a aposta "Doey Don't" apresenta menor volatilidade. Considerando probabilidades de 3-4-5x, aqui está o desvio padrão para ambos os lados:

• Passe + odds completas: 4,915632
• Doey Não: 4,085789

Em resumo, não recomendo o Doey Don't, pois a perda esperada é de 1,36% a mais por unidade.

> [spoiler=Solução]

Deixar:

• p = Probabilidade de o 12 ser rolado primeiro a partir do estado inicial ou sempre que a rolagem anterior não foi um 7.
• q = Probabilidade de sair o 12 primeiro quando o resultado do lançamento anterior foi 7.

Isso é o que se conhece como um problema de Cadeia de Markov.

Antes de prosseguirmos, lembre-se de que a probabilidade de rolar um total de 7 é 1/6 e a de um 12 é 1/36.

Podemos definir p e q em função um do outro, da seguinte forma:

• (1) p = (1/36) + (6/36)q + (29/36)p
• (2) q = (1/36) + (29/36)p

Vamos multiplicar a equação (1) por 36:

36p = 1 + 6q + 29p
(3) 7p = 1 + 6q

Vamos substituir o valor de q em (2) em (3):

7p = 1 + 6*((1/36) + (29/36)p)
7p = 1 + (1/6) + (29/6)p
42p = 6 + 1 + 29p
13p = 7
q = 7/13

Assim, a probabilidade de tirar o 12 primeiro é 7/13 ≈ 53,85%.

A probabilidade de rolar dois 7 consecutivos primeiro é, portanto, de 46,15%.

Assim, é mais provável que o total de 12 seja obtido primeiro.