WOO logo

Recomendações do Mago

Pergunte ao Mago #383

Alice e Bill levam 3 horas para pintar uma casa.
Alice e Cindy levam 4 horas para pintar uma casa.
Bill e Cindy levam 5 horas para pintar uma casa.

Quanto tempo leva se todos eles pintarem?

anônimo

120/47 =~ 2,553191 horas

Aqui está minha solução (PDF).

Um elástico é esticado sobre dois círculos adjacentes de diâmetros 2 e 5. Qual é o comprimento do elástico esticado?

anônimo

2*sqrt(40) + 10*(π - cos -1 (3/7)) =~ 37,297725

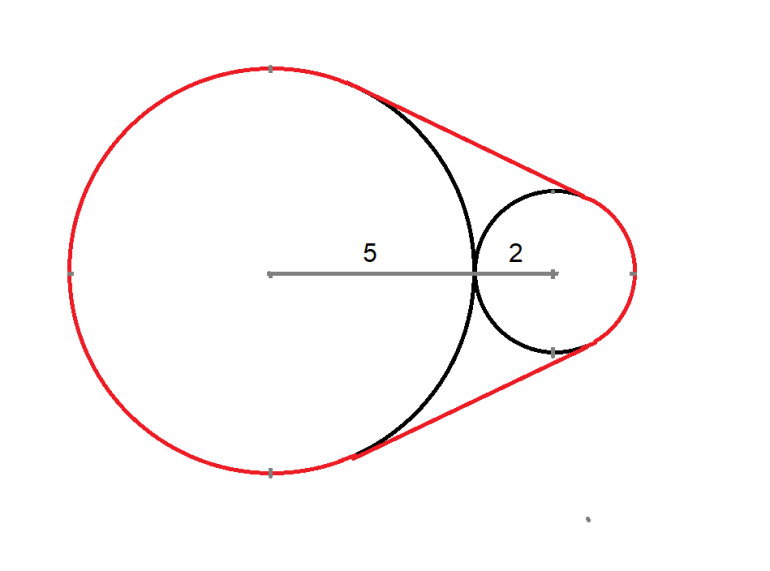
Aqui está minha solução (PDF).

Este problema é abordado e discutido no meu fórum, Wizard of Vegas .

Considere um jogo de pedra-papel-tesoura onde:

  • Se pedra vence tesoura, tesoura paga US$ 1 para pedra.
  • Se a tesoura vence o papel, o papel paga à tesoura US$ 2.
  • Se o papel vencer a pedra, a pedra paga ao papel $3.
  • Em caso de empate, não há troca de dinheiro.

Suponha que dois lógicos estejam jogando. Qual é a estratégia ideal para cada um?

anônimo

  • Jogue papel com probabilidade 1/6
  • Jogue pedra com probabilidade 1/3
  • Jogue tesoura com probabilidade 1/2

Vamos definir algumas probabilidades para o lógico que busca maximizar seus ganhos:

  • r = Probabilidade de jogar rock
  • p = Probabilidade de jogar papel
  • s = Probabilidade de jogar tesoura

É evidente que r+p+s = 1. Dados r e p, s = 1-rp.

Se dois lógicos jogarem, ambos serão indiferentes à jogada do oponente, supondo que eles aleatorizem suas escolhas.

A vitória esperada do oponente ao jogar pedra é: 3p-(1-rp) = 4p+r-1

A vitória esperada do oponente na jogada é: 2(1-rp) - 3r = 2-5r-2p

A vitória esperada do oponente jogando tesoura é: r - 2p

Essas três equações devem ser iguais.

Igualando o primeiro e o terceiro, obtemos:

4p + r - 1 = r - 2p

p = 1/6

Igualando o primeiro e o segundo, obtemos:

2 - 5r - 2p = 4p + r - 1

Já sabemos que p=1/6, o que nos leva facilmente a r=1/3.

s=1-rp = 1-(1/3)-(1/6) = 1/2.

Portanto, ambos devem jogar papel com probabilidade de 1/6, pedra com 1/3 e tesoura com 1/2.

A regra geral para este quebra-cabeça é jogar cada opção de acordo com o peso da quantia de dinheiro que mudaria de mãos se os OUTROS dois símbolos fossem jogados.

Este problema é abordado e discutido no meu fórum, Wizard of Vegas .