Recomendações do Mago
-
Bônus de boas-vindas de $11000 -
Bônus de boas-vindas de 3000 $ -
BÔNUS DE ATÉ $777
Pergunte ao Mago #388
Nessa imagem, qual é o lucro obtido pela empresa de câmbio?
Para o benefício de outros, deixe-me explicar como ler a tabela. Presumo que esta tabela mostre a cotação de compra e venda de moedas estrangeiras em relação à Libra Esterlina (£), já que essa moeda não está listada. Vejamos os valores em dólar americano ($), por exemplo. A tabela indica que eles vendem £1 por $1,5085 e vendem £1 por $1,2658.
Supondo que o lucro seja o mesmo de qualquer forma, o retorno esperado, na falta de um termo melhor, é a raiz quadrada da razão entre o menor e o maior número. Neste caso, sqrt(1,2658/1,5085) = 91,60%. A diferença em relação a 100% é o lucro da casa de câmbio, ou a "vantagem da casa", usando um termo de jogos de azar, que neste exemplo é de 8,40%.
Retorno esperado e vantagem da casa no câmbio
| País | Comprar | Vender | Esperado Retornar | Casa Borda |
|---|---|---|---|---|
| Euro | 1,1800 | 0,9959 | 91,87% | 8,13% |
| EUA | 1,5085 | 1,2658 | 91,60% | 8,40% |
| África do Sul | 15,7723 | 12,3244 | 88,40% | 11,60% |
| Hong Kong | 11,6445 | 9,8024 | 91,75% | 8,25% |
| Japão | 134,6200 | 108,9200 | 89,95% | 10,05% |
| Austrália | 2,3282 | 1,8738 | 89,71% | 10,29% |
| Canadá | 1,8868 | 1,5510 | 90,67% | 9,33% |
| Suíça | 1,8179 | 1,4372 | 88,91% | 11,09% |
| Emirados Árabes Unidos | 5,5920 | 4,4792 | 89,50% | 10,50% |
| Arábia Saudita | 5,8807 | 4,5588 | 88,05% | 11,95% |
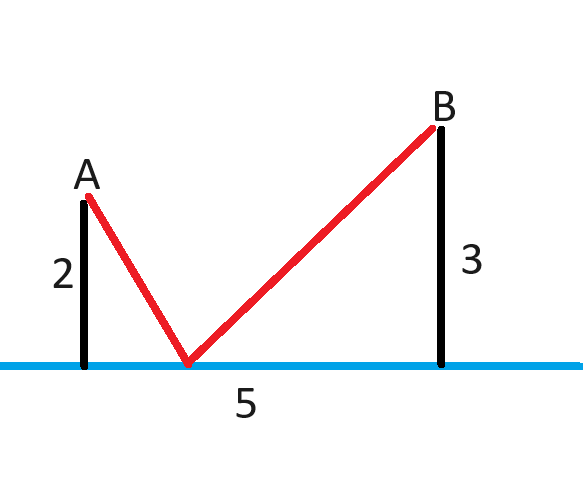
Existe um cano de água reto (azul) próximo aos pontos A e B. O ponto A está a 2 milhas do ponto mais próximo no cano. O ponto B está a 3 milhas do ponto mais próximo no cano. Os dois pontos ao longo do cano que marcam os pontos mais próximos de A e B estão a 5 milhas de distância um do outro. Deseja-se instalar dois novos canos (vermelhos), ligando A e B ao cano de água, com apenas um ponto de contato com o cano de água, e os dois novos canos indo diretamente para A e B. Em outras palavras, os novos canos devem formar um V. Qual é a distância mínima de cano necessária?
Aqui está minha solução (PDF)
Existe um cano de água reto (azul) próximo aos pontos A e B. O ponto A está a 2 milhas do ponto mais próximo no cano. O ponto B está a 3 milhas do ponto mais próximo no cano. Esses dois pontos ao longo do cano, que marcam os pontos mais próximos de A e B, estão a 5 milhas de distância um do outro. Deseja-se fornecer água aos pontos A e B instalando novos canos que liguem os pontos A e B a qualquer ponto ao longo do cano azul. Esses novos canos podem ter qualquer formato desejado. Qual é a distância mínima de novos canos necessária?
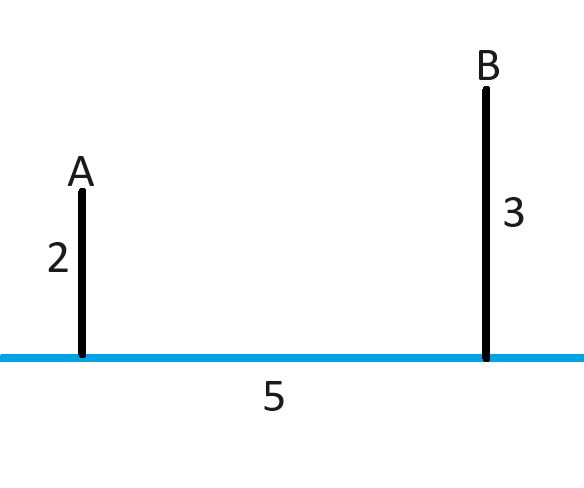
Os novos canos devem formar um "Y", com uma extremidade ligada à tubulação de água existente e as outras duas extremidades ligadas às duas casas.
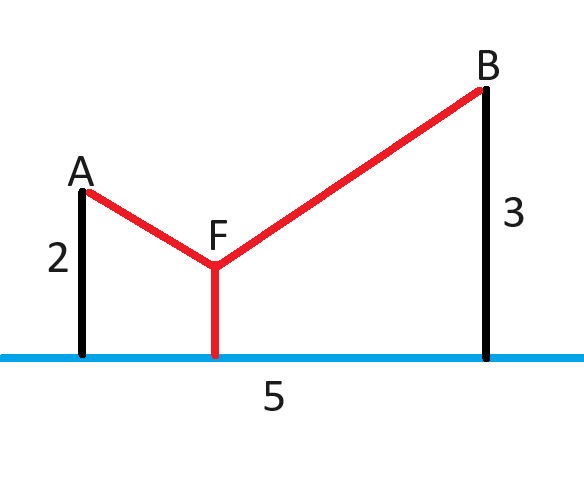
O ponto dentro (ou, em alguns casos, fora) de um triângulo que minimiza a soma das distâncias a cada vértice é chamado de Ponto de Fermat. Não vou explicar como encontrá-lo, mas uma propriedade é que as linhas que ele traça até os três vértices formam três ângulos de 120°.
Para obter mais informações, consulte o verbete da Wikipédia sobre o Ponto de Fermat .
Aqui está minha solução (PDF).