Pergunte ao Mago #395
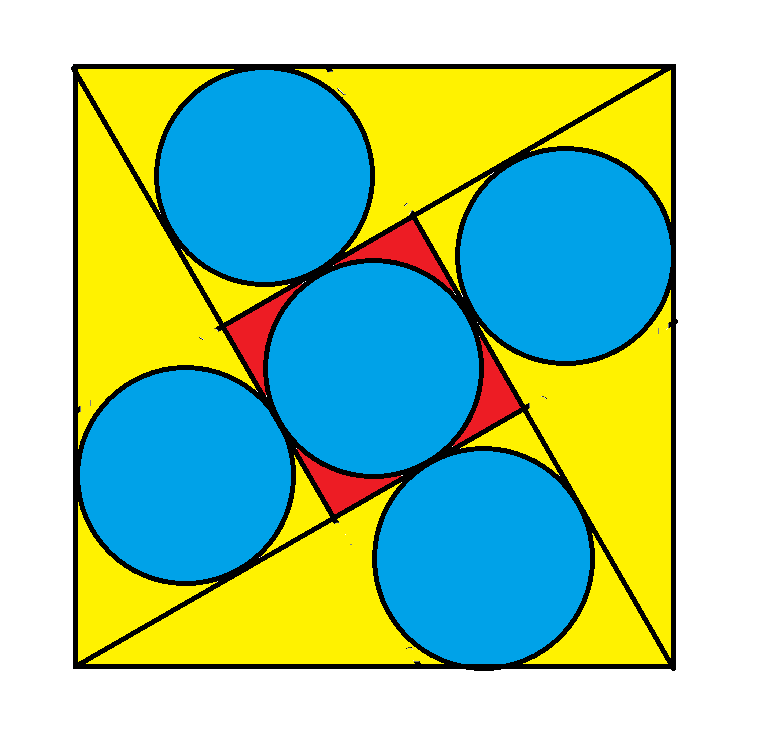
O diagrama acima consiste em quatro triângulos retângulos e um pequeno quadrado dentro de um quadrado maior. O lado do quadrado maior mede 1. Todos os cinco círculos têm o mesmo diâmetro. Qual é o raio desse círculo?
raio = (sqrt(3)-1)/4 =~ 0,183013.
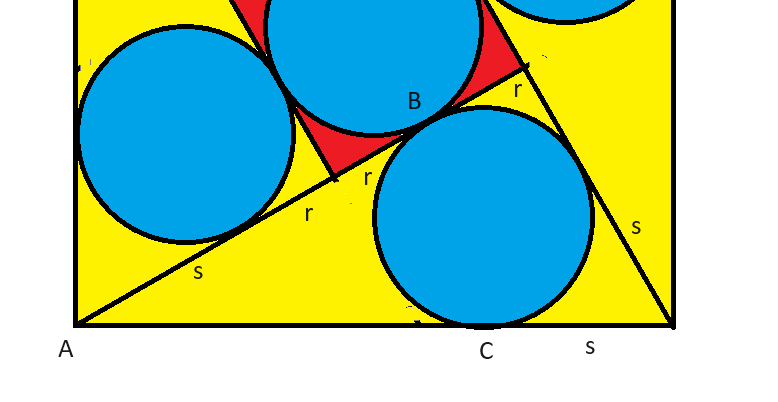 Vamos considerar um dos triângulos. Vamos definir:
Vamos considerar um dos triângulos. Vamos definir:- r = Raio dos círculos
- s = Distância entre qualquer canto do quadrado maior e o ponto onde o círculo mais próximo é tangente ao triângulo em que está inscrito.
Observando o triângulo na imagem, as distâncias são:
- perna curta = r+s
- perna longa = 3r+s
- hipotenusa = 1
Utilizando a fórmula de Pitágoras:
(r+s) 2 + (3r+s) 2 = 1
r² + 2rs + s² + 9r² + 6rs + s² = 1
10r² + 2s² + 8rs = 1
Precisamos de outra equação para resolver isso. Vamos observar o comprimento do quadrado maior, que nos foi dado como 1. AB = AC. AB = 2r + s, então AC = 2r + s. O restante do lado do quadrado maior é s. Portanto:
2r + 2s = 1.
2s = 1-2r
s = 1/2 - r
Vamos substituir esse valor na nossa equação da fórmula de Pitágoras:
10r² + 2(1/2 - r) ² + 8r(1/2 - r) = 1
10r 2 + 2(1/4 - r + r 2 ) + 4r - 8r 2 = 1
2r 2 + 1/2 - 2r + 2r 2 + 4r = 1
4r² + 2r - 1/2 = 0
8r² + 4r - 1 = 0
Usando a equação quadrática:
r = (-4 +/- sqrt(48))/16
r = (sqrt(3)-1)/4 =~ 0,183013.
Este problema foi retirado do canal Mind Your Decisions no YouTube. Presh oferece uma solução que não requer o teorema de Pitágoras.
Este problema é abordado e discutido no meu fórum, Wizard of Vegas .
Qual a sua opinião sobre o "Sistema do Caminho Certo e Errado"? Funciona assim: o jogador faz uma aposta "don't pass" de uma unidade. Se algum ponto for rolado, o jogador aposta uma unidade nesse número. Se o número sair, o jogador lucra e, se sair um sete, recupera o investimento. Parece um freeroll. O que estou perdendo?
Vamos supor, generosamente, que se o ponto for 4 ou 10, o jogador paga a comissão de 5% apenas sobre a vitória. Seguiremos a regra de Las Vegas, onde um 12 na rodada inicial resulta em empate na aposta "don't pass" (no norte de Nevada, o empate ocorre no 2). Dito isso, aqui estão todos os resultados possíveis:
- Se sair um 2 ou 3 no dado: o jogador ganha uma unidade na aposta "don't pass".
- Ao sair um lançamento de 12, o jogador empata na aposta "don't pass".
- Se sair um 7 ou um 11 no dado, o jogador perde a aposta "don't pass".
- Ponto de 4 ou 10 e pontos ganhos: O jogador ganha 1,95 unidades na aposta de compra e perde uma unidade na aposta "não passe", resultando em um lucro líquido de 0,95 unidades.
- Ponto de 5 ou 9 e pontos vencedores: O jogador ganha 1,4 unidades na aposta de lugar e perde uma unidade na aposta "não passe", resultando em um lucro líquido de 0,4 unidades.
- Ponto de 6 ou 8 e pontos vencem: O jogador ganha 7/6 unidades na aposta de lugar e perde uma unidade na aposta "não passe", resultando em um ganho líquido de 1/6 de unidades.
- Ponto de 4 ou 10 e perda de ponto: O jogador perde 1 unidade na aposta de compra e ganha uma unidade na aposta "não passe" por empate na rede.
- Ponto de 5 ou 9 e perda de ponto: O jogador perde 1 unidade na aposta de lugar e ganha uma unidade na aposta "don't pass for net push".
- Ponto de 6 ou 8 e perda de ponto: O jogador perde 1 unidade na aposta de lugar e ganha uma unidade na aposta "don't pass for net push".
A tabela a seguir resume todos os resultados possíveis. A tabela mostra a probabilidade, o ganho e a contribuição para o retorno em todos os resultados possíveis. A célula inferior direita mostra uma perda esperada de 0,02951 unidades.
Sistema de Caminho Certo e Errado
| Evento | Paga | Probabilidade | Retornar |
|---|---|---|---|
| Apareçam 2 ou 3 | 1 | 0,083333 | 0,083333 |
| Saia às 12h | 0 | 0,027778 | 0,000000 |
| Venha às 7 ou às 11. | -1 | 0,222222 | -0,222222 |
| Ponto 4 vitória | 0,95 | 0,027778 | 0,026389 |
| Vitória do ponto 5 | 0,4 | 0,044444 | 0,017778 |
| Vitória do ponto 6 | 0,166667 | 0,063131 | 0,010522 |
| Vitória do ponto 8 | 0,166667 | 0,063131 | 0,010522 |
| Vitória do ponto 9 | 0,4 | 0,044444 | 0,017778 |
| Vitória do ponto 10 | 0,95 | 0,027778 | 0,026389 |
| Ponto 4 de perda | 0 | 0,055556 | 0,000000 |
| Ponto 5 de perda | 0 | 0,066667 | 0,000000 |
| Ponto 6 de perda | 0 | 0,075758 | 0,000000 |
| Ponto 8 perda | 0 | 0,075758 | 0,000000 |
| Ponto 9 de perda | 0 | 0,066667 | 0,000000 |
| Ponto 10 perda | 0 | 0,055556 | 0,000000 |
| Total | 1.000000 | -0,029512 |
A razão pela qual essa estratégia tem um valor esperado negativo reside na rodada inicial (come out roll). Há 3 maneiras de ganhar com um 2 ou 3 e 8 maneiras de perder com um 7 ou 11. É verdade que, se o jogador sobreviver à rodada inicial, ele terá um saldo positivo, mas isso não é suficiente para compensar a perda esperada nessa rodada.
Minha esposa fica com raiva 20% do tempo. Quando perguntada "Você está com raiva?", ela responde "não" em 90% das vezes quando está com raiva. Quando a mesma pergunta é feita quando ela não está com raiva, ela responde "não" em 95% das vezes. Minha pergunta é: qual a probabilidade de ela estar com raiva de acordo com a resposta à pergunta?
Esta é uma questão clássica de probabilidade Bayesiana.
Se ela responder "não", a probabilidade de ela estar zangada é de 9/47 = 19,15%.
Se ela responder "sim", a probabilidade de ela estar zangada é de 1/3 = 33,33%.
A fórmula para a resposta a perguntas expressas como "se A então B" é probabilidade(tanto A quanto B)/probabilidade(B).
No caso de uma resposta "não", a probabilidade de ela estar brava é (0,2*0,9)/(0,2*0,9 + 0,8*0,95) = 0,18/0,94 = 9/47.
No caso de uma resposta "sim", a probabilidade de ela estar brava é (0,2*0,1)/(0,2*0,1 + 0,8*0,05) = 0,02/0,06 = 1/3.


