Pergunte ao Mago #399
Se você remover o pequeno quadrado da primeira imagem e reorganizar as peças, a área total ainda parecerá a mesma. Como isso é possível?
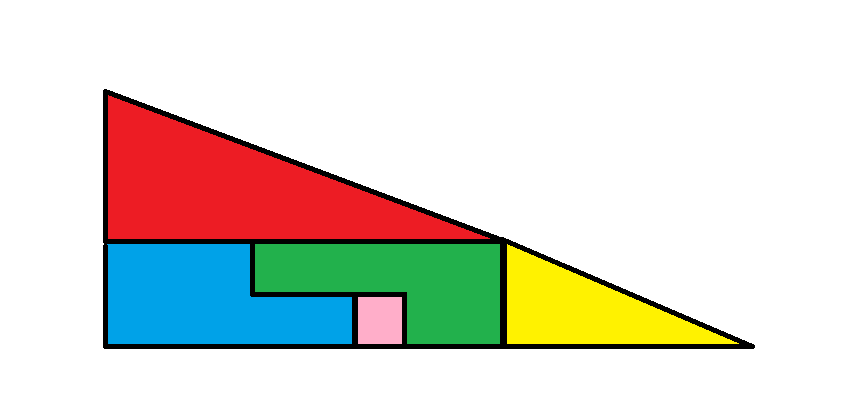
Imagem 1
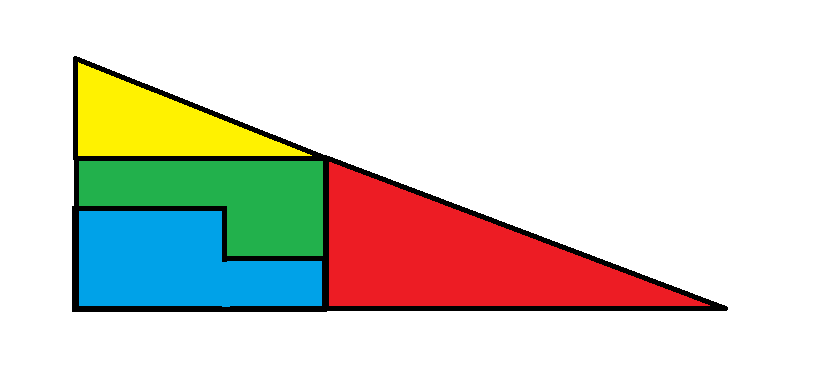
Imagem 2
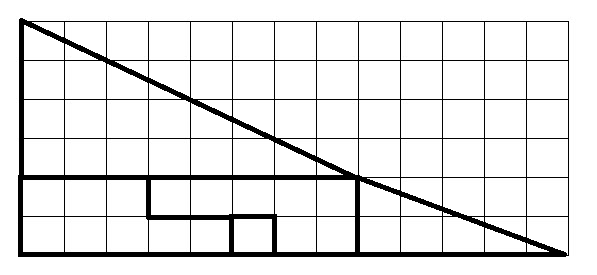
A imagem acima mostra a primeira imagem em uma grade, para melhor visualizar o tamanho de cada peça.
Observe que o triângulo vermelho maior tem lados de comprimento 4 e 8. Observe também que o triângulo amarelo menor tem lados de comprimento 2 e 5. Em outras palavras, os triângulos não são proporcionais. A hipotenusa dos dois triângulos não tem a mesma inclinação, conforme mostrado em cada figura. Uma tem inclinação 0,5 e a outra 0,4. Ao posicionar as peças como estão em cada figura, parece que elas formam um triângulo maior com lados de 5 e 13, mas não se trata de um triângulo.
A área do triângulo vermelho é 4*8/2 = 16.
A área do triângulo amarelo é 2*5/2 = 5.
Na primeira imagem, as outras três peças formam um retângulo de tamanho 2 por 8, totalizando uma área de 16.
Na segunda imagem, as outras duas peças formam um retângulo de tamanho 3 por 5, totalizando uma área de 15.
A área total da primeira imagem é triângulo vermelho + triângulo amarelo + retângulo grande = 16 + 5 + 16 = 37.
A área total da segunda imagem é triângulo vermelho + triângulo amarelo + retângulo pequeno = 16 + 5 + 15 = 36.
Em resumo, a primeira imagem é maior por causa do quadrado pequeno. Trata-se de uma ilusão de ótica que dá a impressão de que as partes juntas formam um triângulo grande em ambos os casos. Mas não formam.
Há 16 motocicletas na orla de um grande deserto. Cada motocicleta pode percorrer 160 quilômetros (100 milhas) com um tanque de gasolina. Todas as motocicletas começam com o tanque cheio. É permitido transferir gasolina entre as motocicletas. O objetivo é levar uma motocicleta o mais longe possível do ponto de partida. Qual a distância que ela consegue percorrer?
A chave para resolver o problema é o grupo se deslocar por uma curta distância. Depois, basta pegar o combustível restante de uma das motocicletas e completar os tanques das outras.
Por exemplo, no início, divida um tanque cheio de gasolina em 16 partes, uma para cada motocicleta. Em seguida, todos dirigem juntos até que 1/16 do tanque seja consumido, o que dará ao grupo 100/16 = 6,25 milhas. Retire 15/16 do tanque de uma motocicleta e transfira 1/16 do tanque para as outras 15 motocicletas, completando assim o tanque de cada uma.
Em seguida, repita o mesmo processo, mas com 15 motocicletas restantes, percorra a distância que 1/15 de um tanque permitir, que é 100/15 = 6,666667 milhas. Depois, retire mais 14/15 de um tanque de uma motocicleta e transfira 1/15 de tanque para as outras 14 motocicletas.
Continuando neste processo, a última motocicleta terá percorrido uma distância total de (1/16) + (1/15) + (1/14) + ... + (1/1) =~ 338,072899 milhas.
Essa pergunta foi feita e discutida no meu fórum no Wizard of Vegas .
O que você acha do Paradoxo da Bela Adormecida?
Para benefício de outros leitores, aqui está o que está sendo perguntado no Problema/Paradoxo da Bela Adormecida.
A Bela Adormecida (BA) se oferece como voluntária para um experimento. Todos os detalhes do experimento são explicados a ela de forma verídica, como segue:
- Domingo: SB será eutanasiada. Depois que ela adormecer, uma moeda honesta será lançada.
- Segunda-feira: SB será acordada na segunda-feira e perguntada: "Qual a probabilidade de a moeda ter caído em cara?". Após responder, ela será colocada para dormir novamente com um medicamento que induz amnésia, fazendo com que ela se esqueça de tudo o que aconteceu na segunda-feira.
- Terça-feira: Se a moeda cair em coroa, acontecerá novamente o mesmo que aconteceu na segunda-feira. Se cair em cara, ela dormirá o dia inteiro.
- Quarta-feira: SB é acordado novamente, não lhe perguntam nada e ele vai para casa, pois o experimento terminou.
A questão é: como ela deve responder à pergunta feita na segunda-feira e talvez na terça-feira?
Minha resposta
Se esse experimento fosse repetido milhões de vezes, poderíamos esperar observar três tipos de despertares, cada um com a mesma probabilidade de ocorrer:
- A moeda cai em cara, despertando na segunda-feira.
- Se a moeda cair em coroa, o valor será divulgado na segunda-feira.
- A moeda cai em coroa, despertando na terça-feira.
Isso ocorre porque os despertares de segunda-feira devem ser divididos igualmente entre o resultado de cara e coroa no lançamento de uma moeda. Além disso, se a moeda cair em coroa, os despertares de segunda e terça-feira serão exatamente iguais. Assim, todos os três grupos terão aproximadamente o mesmo número de despertares em uma amostra grande.
Desses despertares, um em cada três ocorre após sair cara no lançamento da moeda. Portanto, a probabilidade de a moeda cair em cara é de 1/3.
O grupo que defende a hipótese do "1/2" argumenta que SB não recebe nenhuma informação adicional a cada despertar e, portanto, deve presumir que cada resultado da inversão era igualmente provável.
Além disso, eu ampliaria o problema para 999.999 despertares caso a moeda caísse em coroa. Apenas 1 em um milhão de despertares ocorreria após um lançamento de cara. Portanto, seria bastante fácil presumir que qualquer despertar provavelmente se tratava de um dos 999.999 despertares após um lançamento de coroa. Em outras palavras, a resposta correta neste caso seria 1 em 1.000.000.
Para oferecer outra extensão, imagine que SB fosse solicitada a prever o resultado do lançamento de uma moeda a cada despertar. Se acertasse, ganharia US$ 1.000. Se tivesse uma estratégia para dizer "cara", poderia esperar ganhar (1/2) * US$ 1.000 = US$ 500. Se tivesse uma estratégia para dizer "coroa", poderia esperar ganhar (1/2) * US$ 2.000 = US$ 1.000. Portanto, o simples fato de SB estar desperta favorece que a moeda caia em coroa.
Caso minha explicação não tenha sido clara, o Problema da Bela Adormecida na Wikipédia aborda o assunto com muito mais profundidade do que eu, incluindo outras possíveis respostas da Bela Adormecida.
Essa pergunta foi feita e discutida no meu fórum no Wizard of Vegas .


