Pergunte ao Mago #402

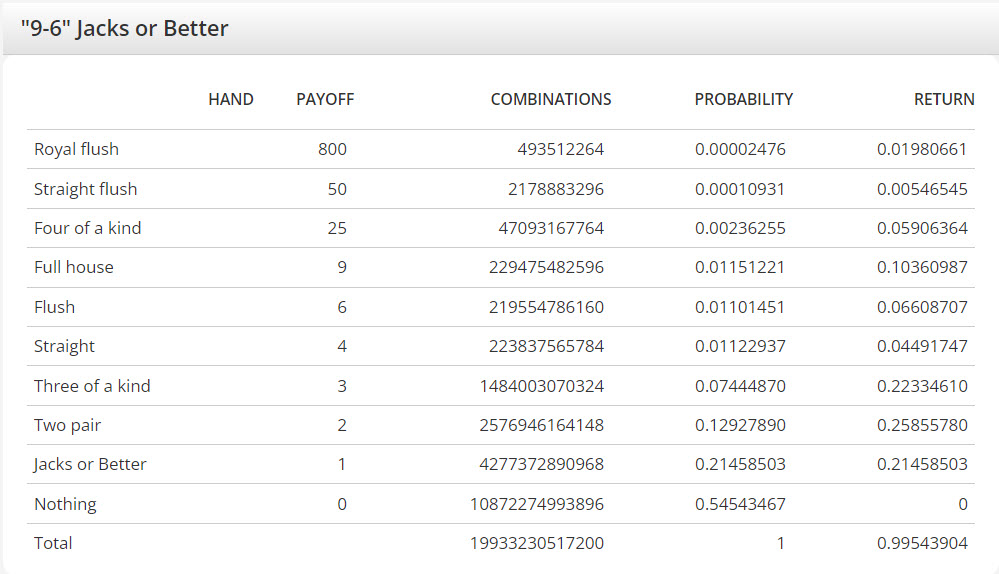
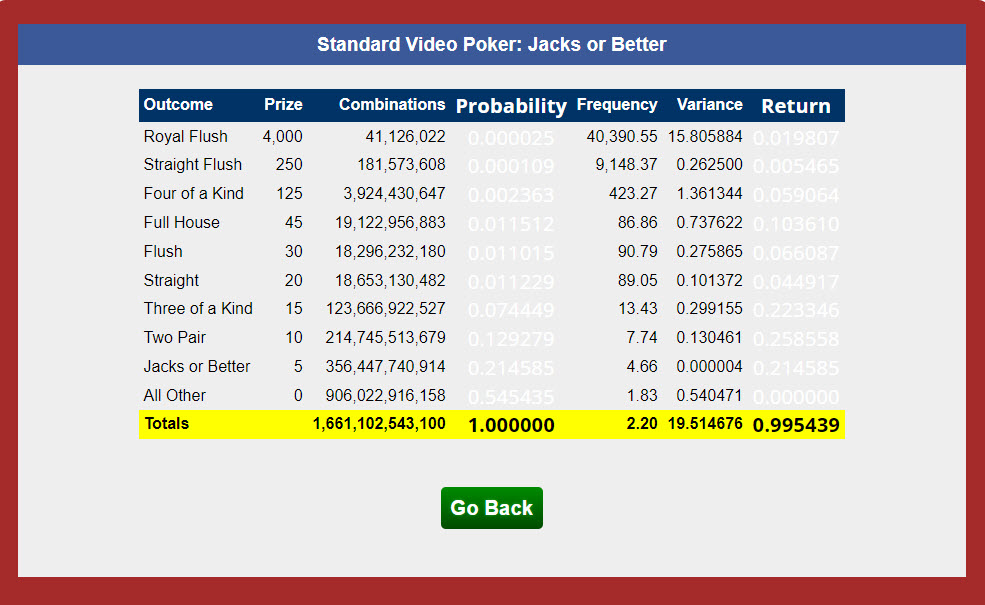
Na sua calculadora de vídeo pôquer para 9-6 Jacks or Better, a sua mesa mostra 1.661.102.543.100 como o número total de combinações. Enquanto isso, a sua página do Jacks or Better mostra 19.933.230.517.200 como o número total de combinações. Parece-me que o número de combinações deveria ser o mesmo. Gostaria de saber por que essa diferença? O retorno (0,995439) parece ser o mesmo.

IndyJeffrey

Sim, as duas fontes abordam o mesmo jogo.

A razão está relacionada à forma como o jogo é analisado. Quanto mais cartas o jogador descarta, maior o número de combinações possíveis na próxima compra. A tabela a seguir mostra o número de combinações possíveis na próxima compra, ou seja, o número de maneiras de escolher a quantidade de cartas a serem descartadas dentre as 47 cartas restantes no baralho.

Descarta	Combinações no sorteio	Ponderação
0	1	7.669.695
1	47	163.185
2	1.081	7.095
3	16.215	473
4	178.365	43
5	1.533.939	5

O mínimo múltiplo comum de 1, 47, 1081, 16215, 178365 e 1533939 é 7669695.

É importante que cada mão inicial tenha a mesma ponderação total. Para isso, aplico um fator de ponderação a cada mão, de acordo com o número de descartes. Esse fator de ponderação está na coluna da direita da tabela acima. O produto do número de combinações no descarte pelo fator de ponderação será sempre 7.669.695.

Existem combin(52,5) = 52!/(47!*5!) = (48*49*50*51*52)/(1*2*3*4*5) = 2.598.960 maneiras de escolher cinco cartas dentre 52. Portanto, o número total de combinações no vídeo pôquer, da forma como analiso, é combin(52,5)*combin(47,5)*5 = 2.598.960 * 7.669.695 = 19.933.230.517.200. É por isso que você vê esse número com tanta frequência como o total de combinações nas minhas tabelas de retorno.

Então, por que a calculadora mostra 1.661.102.543.100, você pode se perguntar? O gênio da programação de vídeo pôquer, JB, criou essa calculadora. Ele adicionou uma etapa para encontrar o maior múltiplo comum das combinações de cada mão. Esse menor múltiplo comum geralmente era 12. Seja qual fosse o valor, ele dividia cada número de combinações por esse menor múltiplo comum. Acho que é porque ele gosta de manter os números o menor possível, sem sacrificar a precisão.

Há um elástico de um metro de comprimento com uma formiga em uma das extremidades. A cada dia, a formiga percorre um centímetro. Ao final do dia, o elástico está esticado em um metro. Quanto tempo levará para a formiga chegar à outra extremidade?

anônimo

Aviso: este é um problema bastante difícil. No quadro de spoilers abaixo, dou algumas dicas para ajudá-lo a resolvê-lo.

Série Harmônica

Constante de Euler (não confundir com o número de Euler)

15.092.688.622.113.800.000.000.000.000.000.000.000.000.000

Aqui está minha solução (PDF).

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .

Recentemente, eu e meu amigo conseguimos dois dos três símbolos Megabucks. Qual a probabilidade disso acontecer?

Hot Blonde de Las Vegas

De acordo com a minha página sobre Megabucks , o peso total de cada rolo é 368, sendo que os símbolos Megabucks têm um peso de 1. Portanto, a probabilidade de um rolo parar nos símbolos Megabucks é de 1/368.

A probabilidade de obter exatamente 2 de 3 é 3 × (1/368) * (1/368) × (367/368) =~ 0,0000220924 =~ em 1/45.264.