WOO logo

Recomendações do Mago

Pergunte ao Mago #405

x² - 3 = sqrt(x+3). Resolva para x.

anônimo

Seja y igual a ambas as expressões. Assim, temos:

  • y = x^2 - 3
  • y = sqrt(x+3)

Observe o número 3 em ambas as expressões. Vamos expressar ambas as equações com um 3 em um dos lados. Primeiro temos:

3 = x² - y

Em seguida, vamos elevar ao quadrado a segunda equação acima:

y² = x + 3

3 = y² - x

Vamos igualar as duas expressões para 3:

x² - y = y² - x

Vamos reorganizar:

x² - y² + x - y = 0

(x+y)(xy) + x - y = 0

(xy)(x+y+1) = 0

Primeiro, vamos examinar xy = 0:

xy = 0

Vamos substituir y = x^2 - 3 por y.

x - (x^2 - 3) = 0

x² - x - 3 = 0

Utilizando a fórmula de Pitágoras:

x = (1 +/- sqrt(1 + 12)/2

x = (1 + sqrt(13)/2 e x = (1 - sqrt(13)/2

Em segundo lugar, vamos examinar x+y+1 = 0:

Vamos substituir y = x^2 - 3 por y.

x + (x^2 - 3) + 1 = 0

x + x² - 3 + 1 = 0

x² + x - 2 = 0

Utilizando a fórmula de Pitágoras:

x = (-1 +/- sqrt(1 + 8)/2

x = (-1 +/- 3)/2

x = 1, x = -2

Portanto, nossas quatro respostas são:

  • x = 1
  • x = -2
  • x = (1 + sqrt(13)/2 =~ 2,302776
  • x = (1 - sqrt(13)/2 =~ -1,302776

Gostaria de agradecer ao vídeo do YouTube "Solving x^2-3=sqrt(x+3)" do SyberMath por este método para resolver este problema. Vá para o minuto 6:28 para ver o método.

Um ponto fora de um círculo de raio 1 consegue ver 1/3 da circunferência. A que distância está esse ponto?

anônimo

A resposta é exatamente 1.

Considere este diagrama para a solução.

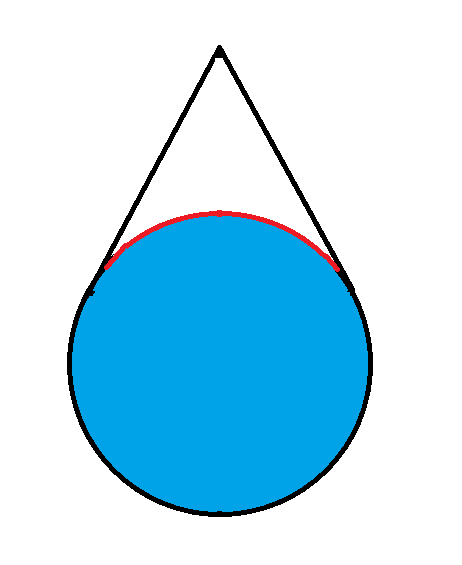
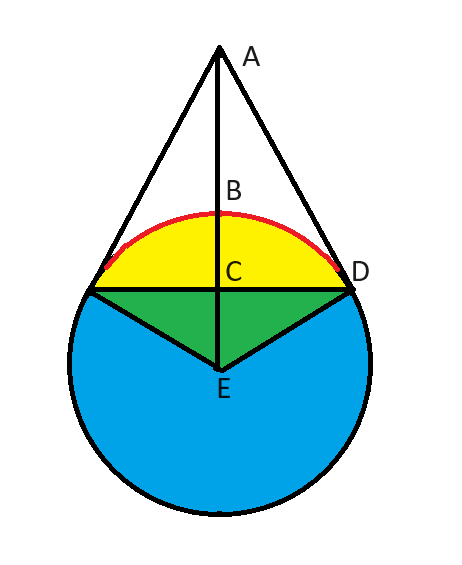
Considere o triângulo ADE. Sabemos que:

  • O ângulo ADE mede 90 graus, porque AD é tangente à circunferência.
  • O ângulo AED é de 60 graus, porque o ângulo do triângulo verde em E é de 120 graus (1/3 do total de 360).
  • O ângulo EAD deve ser igual aos outros 30 graus do triângulo ADE.

Este é o clássico triângulo 30-60-90. Todos nós devemos saber que os lados desse triângulo são proporcionais a 1, 2 e sqrt(3).

Neste caso, ED = 1, conforme indicado na questão. AE é o dobro dessa distância, ou seja, 2.

O valor 2 representa a distância do ponto ao centro da circunferência. A pergunta é qual a distância do ponto ao ponto mais próximo na circunferência. Portanto, subtraímos o raio. Assim, a resposta é 2 - 1 = 1.

Bob e Tom estão atravessando uma ponte ferroviária e estão a 1/3 do caminho desde o ponto de partida. De repente, ouvem um trem vindo por trás deles. Ambos conseguem correr a uma velocidade de 5 milhas por hora. Bob se vira e Tom corre para frente. Ambos escapam do trem por menos de um segundo. Qual era a velocidade do trem?

anônimo

Lembre-se que distância = velocidade * tempo, que expressaremos como d = r * t

Reescrevendo: t = d/r.

O horário é o mesmo tanto para Bob quanto para o trem, no início da ponte:

Vamos deixar:

  • x = distância entre o trem inicialmente e o início da ponte.
  • r = taxa de velocidade do trem

Primeiro, vamos analisar Bob, que volta correndo. Vamos expressar o tempo necessário para que Bob e o trem se encontrem no início da ponte:

Bob: t = (1/3)/5

Trem: t = x/r

Igualando as duas expressões para t:

(1/3)/5 = x/r

r/3 = 5x

r = 15x

Em segundo lugar, vejamos Tom, que corre à frente. Vamos expressar o tempo necessário para que Tom e o trem se encontrem no início da ponte:

Tom: t = (2/3)/5

Trem: t = (1+x)/r

Igualando as duas expressões para t:

(2/3)/5 = (1+x)/r

2r/3 = 5(1+x)

2r = 15(1+x)

2r = 15 + 15x

Neste momento temos:

  • r = 15x
  • 2r = 15 + 15x

Vamos substituir a expressão para r na primeira equação na segunda:

30x = 15 + 15x

15x = 15

x = 1

Lembre-se, r = 15x.

Portanto, a velocidade do trem é de 15*1 = 15 mph.