Pergunte ao Mago #410
Vejo que você respondeu a uma pergunta sobre o jogo Plinko no programa "The Price is Right" na coluna "Ask the Wizard" nº 115. No entanto, às vezes eles alteram os valores dos prêmios em programas especiais. Por exemplo, na Semana do Grande Prêmio, os prêmios, da esquerda para a direita, eram: $500, $1000, $2500, $0, $200000, $0, $2500, $1000 e $500. Qual seria o valor esperado para cada posição de onde o disco é lançado? Qual é a probabilidade de o disco cair em qualquer prêmio, dada qualquer posição inicial?
Existem nove posições iniciais para lançar o disco. No entanto, precisamos nos concentrar apenas em cinco, pois os prêmios e a disposição dos pinos são simétricos. Vamos numerá-las, começando pela borda esquerda, de 1 a 5.
Existem também nove posições finais; vamos numerar as cinco primeiras, da esquerda para a direita, de 1 a 5.

A tabela a seguir mostra a probabilidade de aterrissar em qualquer ponto específico (coluna da esquerda) de acordo com a posição de onde o objeto foi solto (linha superior).
| Ponto de aterrissagem | Escolha 1 ou 9 | Escolha 2 ou 8 | Escolha 3 ou 7 | Deixe cair 4 ou 6 | Deixe cair 5 |
|---|---|---|---|---|---|
| 1 ou 9 | 0,225586 | 0,193359 | 0,121094 | 0,056641 | 0,032227 |
| 2 ou 8 | 0,386719 | 0,346680 | 0,250000 | 0,153320 | 0,113281 |
| 3 ou 7 | 0,242188 | 0,250000 | 0,257813 | 0,250000 | 0,242188 |
| 4 ou 6 | 0,113281 | 0,153320 | 0,250000 | 0,346680 | 0,386719 |
| 5 | 0,032227 | 0,056641 | 0,121094 | 0,193359 | 0,225586 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
A próxima tabela mostra o valor esperado de cada posição de lançamento para a Semana do Grande Prêmio que você mencionou. Como esperado, o jogador deve lançar o disco na direção do maior prêmio.
| Local de entrega | Vitória esperada |
|---|---|
| 1 ou 9 | $ 7.550,29 |
| 2 ou 8 | $ 12.396,48 |
| 3 ou 7 | $ 25.173,83 |
| 4 ou 6 | $ 39.478,52 |
| 5 | $ 45.852,05 |
O que é o paradoxo da trombeta de Gabriel?
Considere primeiro a curva definida pela equação y = 1/x para valores de x de 1 ao infinito. Esse gráfico terá a seguinte aparência para valores de x até 17.
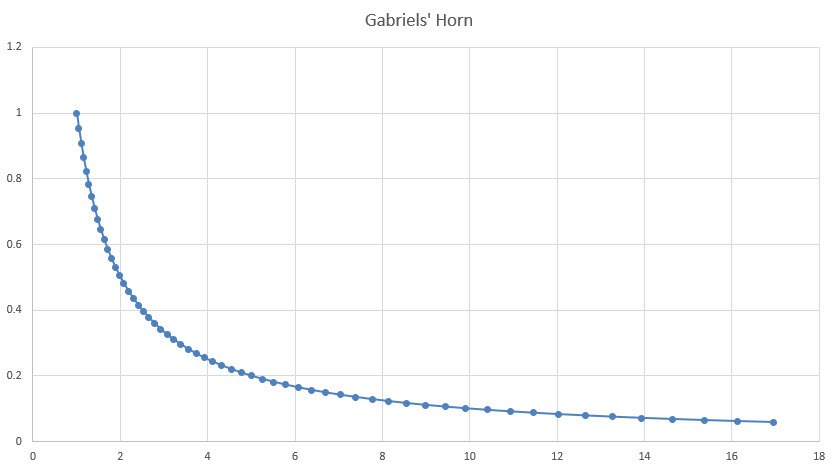
Agora, imagine essa curva sendo rotacionada em torno do eixo x. Ela criará algo parecido com uma trombeta, com uma extremidade infinitamente longa. É a isso que os matemáticos chamam de Trombeta de Gabriel.

Fonte da imagem: Soul of Mathematics .
Em seguida, considere as questões sobre a Trombeta de Gabriel:
- Qual é o volume?
- Qual é a área da superfície?
Aqui estão as respostas:
- Volume = π = pi.
- Área da superfície = infinito
Meu trabalho demonstrando essas respostas pode ser encontrado aqui (PDF).
A natureza do paradoxo questiona como o volume pode ser finito e a área da superfície infinita?
O paradoxo aparente surge quando confundimos duas dimensões com três. Simplesmente não devemos fazer isso. Considere o círculo A com raio 1 e o círculo B com raio 1,1, onde o círculo A está contido no círculo B.
O círculo A tem uma circunferência de 2π ≈ 6,283185 e o círculo B tem uma área de 1,1²π ≈ 3,801327. Observe que o círculo B é maior que o círculo A, porém sua área é menor que a circunferência de B. Não se trata de a circunferência de B ser parte da área de A. Área e circunferência são medidas diferentes em dimensões diferentes e não devem ser comparadas.
Outra forma de ver isso é que, se fizéssemos um disco a partir do círculo A com um número infinito de sulcos, o comprimento desses sulcos seria infinito.
Voltando à Trombeta de Gabriel, considere simplificá-la para o caso discreto de círculos com raios 1, 1/2, 1/3, 1/4...
A soma dos volumes desses círculos seria pi*(1/1 + 1/4 + 1/9 + 1/16 + ...). Existe uma conhecida série infinita que diz:
1/1 + 1/4 + 1/9 + 1/16 + ... = pi^2/6 ≈ 1,644934.
Adicionando outro termo pi, a soma das áreas dos círculos é pi^3/6 ≈ 5,167713.
Entretanto, a soma das circunferências é 2*pi(1/1 + 1/2 + 1/3 + 1/4 + ...).
Trata-se de outra série infinita bem conhecida na matemática, chamada Série Harmônica, que afirma:
1/1 + 1/2 + 1/3 + 1/4 + ... = ∞ = infinito.
2*pi*∞ ainda é igual a ∞.
Se estendermos essa lógica para distâncias infinitamente pequenas entre círculos, obtemos a Trombeta de Gabriel.
Nathan compra 100 libras de feijão. O feijão é composto por 99% de água em peso. Ela os deixa ao sol para secarem. No dia seguinte, ela descobre que eles são compostos por 98% de água. Qual é o novo peso deles?
Deixar:
- w = Peso original da água.
- w' = Peso da água após a secagem dos grãos.
- x = Peso de todos os outros componentes do feijão.
Para o primeiro dia, nos é dado:
w + x = 100
w/(w+x) = 0,99
Substituindo a primeira equação na segunda:
w/100 = 0,99
w = 99
Portanto, x=1.
No dia seguinte, nos é dado:
w'/(w'+x) = 0,98
w' = 0,98*(w'+x)
0,02w' = 0,98x
Sabemos que x=1, então:
0,02w' = 0,98
w' = 0,98/0,02 = 49
O peso total no dia seguinte é x+w' = 1+49 = 50.


