Recomendações do Mago
-
Bônus de boas-vindas de $11000 -
Bônus de boas-vindas de 3000 $ -
BÔNUS DE ATÉ $777
Pergunte ao Mago #412
No bacará, qual é a probabilidade de um dos lados (Banca ou Jogador) aparecer pelo menos três vezes mais do que o outro em um sapato?
Peço desculpas se eu fizer apenas uma estimativa neste caso.
Em média, um sapato contém 80,88 mãos. Em média, 7,70 mãos terminam em empate, resultando em 73,18 vitórias combinadas do Banqueiro e do Jogador. Para que um lado tenha o triplo de vitórias em relação ao outro, isso precisaria ocorrer 54,89 vezes e o outro 18,30 vezes.
Em 73,18 apostas resolvidas, podemos esperar 37,09 vitórias do Banqueiro e 36,09 vitórias do Jogador. Um desvio padrão para ambos é de 4,28. Para atingir 54,89 vitórias ou mais, seria necessário estar 4,16 desvios padrão acima das expectativas para o Banqueiro e 4,39 para o Jogador. A probabilidade de qualquer um dos lados estar tantos desvios padrão acima das expectativas é de aproximadamente 1 em 47.000.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
A seguir, apresentamos as probabilidades de apostas para o vencedor da eleição presidencial de 2028. Qual a probabilidade de qualquer outro candidato vencer?
| Aposta | Paga |
|---|---|
| Vance | +250 |
| Newsom | +750 |
| Shapiro | +900 |
| Senhor Obama | +1200 |
| Buttigieg | +1400 |
| Whitmer | +1600 |
| Ramaswamy | +1600 |
| DeSantis | +2000 |
Apostas futuras como essa tendem a ter uma vantagem da casa de cerca de 30%. Se adicionássemos uma aposta hipotética no campo com odds de -160, o conjunto geral de apostas teria uma vantagem da casa de 29,95%. A tabela a seguir mostra os detalhes. A "probabilidade implícita" mostra a probabilidade se a aposta fosse exatamente justa. A "probabilidade real" é a probabilidade justa de cada aposta dividida pela soma das probabilidades justas. Isso mostra que a probabilidade de qualquer outra pessoa ganhar é de 43,1%.
| Aposta | Paga | Implícito Probabilidade | Real Probabilidade |
|---|---|---|---|
| Vance | +250 | 0,285714 | 0,200136 |
| Newsom | +750 | 0,117647 | 0,082409 |
| Shapiro | +900 | 0,100000 | 0,070048 |
| Senhor Obama | +1200 | 0,076923 | 0,053883 |
| Buttigieg | +1400 | 0,066667 | 0,046698 |
| Whitmer | +1600 | 0,058824 | 0,041204 |
| Ramaswamy | +1600 | 0,058824 | 0,041204 |
| DeSantis | +2000 | 0,047619 | 0,033356 |
| Campo | -160 | 0,615385 | 0,431062 |
| Total | 1,427602 | 1.000000 |
O retorno total é o inverso da soma das probabilidades implícitas, que é 1/1,427602 ≈ 0,700475. A soma do retorno e da vantagem da casa é 1, portanto a vantagem da casa é 1,000000 - 0,700475 = 0,299524.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Na imagem abaixo, o círculo amarelo tem raio 1. Qual é a área do círculo vermelho?
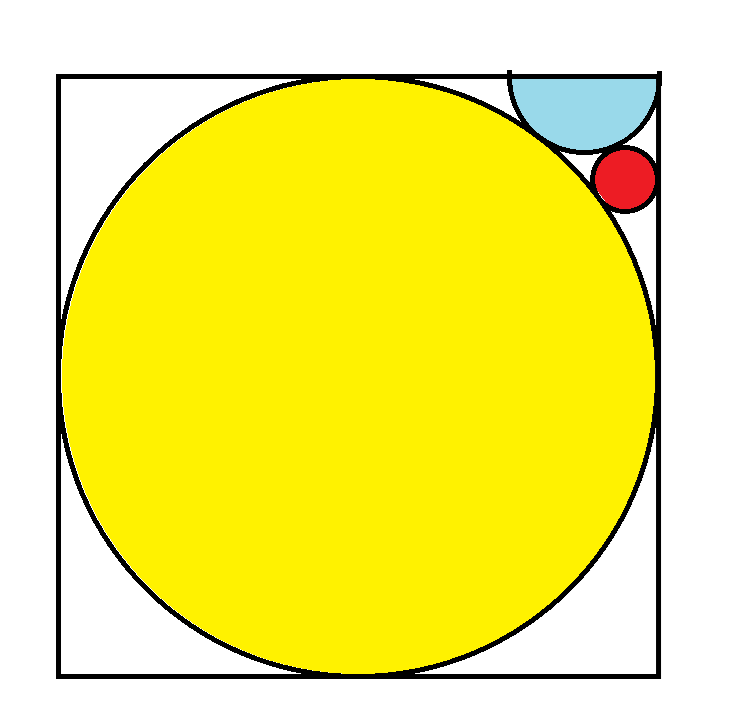
A resposta é π/81 ≈ 0,038785.
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .