WOO logo

Recomendações do Mago

Pergunte ao Mago #413

Existe alguma maneira de fazer uma troca de presentes de Amigo Secreto que atenda aos seguintes requisitos:

  • Ninguém dá um presente a si mesmo.
  • Não há segundas chances.
  • Ninguém sabe de nada, exceto para quem devem comprar.
  • Cada partida tem a mesma probabilidade de sucesso.

anônimo

Sim! Eu chamo isso de método Hannah Fry.

  • Crie um conjunto de cartas como mostrado abaixo. Cada carta deve ter um número único na parte superior e inferior. No exemplo abaixo, o número é 23.
  • Embaralhe as cartas e empilhe-as novamente.
  • Mantendo a pilha intacta, corte cada carta ao longo da linha de referência no meio, criando duas pilhas.
  • Corte e complete o corte de UMA das pilhas.
  • Distribua a carta do topo de cada pilha, uma de cada vez, para cada participante.
  • Crie uma lista numerada e peça a todos que escrevam seu número nela.

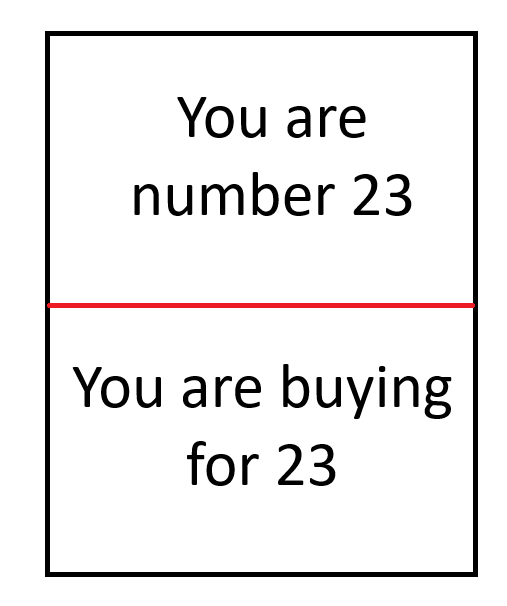
Após esse procedimento, cada pessoa receberá dois cartões com dizeres como, por exemplo, "Você é o número 13" e "Você está comprando para o número 7". Uma vez preenchida a lista, todos saberão para quem comprar, mas não terão ideia de quem está comprando para eles.

Fonte: Os problemas com o Papai Noel Secreto - Numberphile .

Uma piscina está cheia de água salgada. A piscina comporta 1000 metros cúbicos de água. Uma mangueira de jardim despeja água doce na piscina a uma taxa de um metro cúbico por hora. À medida que a água doce entra, a água sai pela outra extremidade na mesma taxa. Quanto tempo leva para a piscina conter apenas 1% de água salgada?

anônimo

A resposta é 2000 ln(10) ≈ 4605,170186 horas ≈ 191,8821 dias.

Aqui está minha solução (PDF).

Em média, quantas rolagens são necessárias em cada um dos sólidos platônicos para rolar qualquer lado que já tenha sido rolado anteriormente?


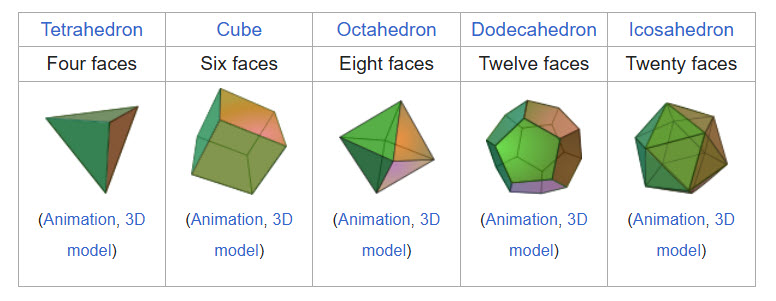
Fonte da imagem: Wikipédia

anônimo

Aqui está a resposta em número de lados.

Lados Rolos médios
4 3,218750
6 3,774691
8 3,846558
12 5.036074
20 6,293585

Vamos analisar o caso específico de um cubo de seis lados.

  • A probabilidade de o experimento terminar em dois lançamentos é de 1/6.
  • A probabilidade de o experimento terminar em três lançamentos é (5/6)*(2/6).
  • A probabilidade de o experimento terminar em quatro lançamentos é (5/6)*(4/6)*(3/6).
  • A probabilidade de o experimento terminar em cinco lançamentos é (5/6)*(4/6)*(3/6)*(4/6).
  • A probabilidade de o experimento terminar em seis lançamentos é (5/6)*(4/6)*(3/6)*(2/6)*(5/6).
  • A probabilidade de o experimento terminar em sete lançamentos é (5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6).

Seja pr(n) = probabilidade de o experimento terminar em n lançamentos.

O número esperado de lançamentos é: 2*pr(2) + 3*pr(3) + 4*pr(4) + 5*pr(5) + 6*pr(6) + 7*pr(7) =

2*(1/6) + 3*(5/6)*(2/6) + 4*(5/6)*(4/6)*(3/6) + 5*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6)*(2/6)*(5/6) + 7*(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) =~ 3,774691358.