WOO logo

Recomendações do Mago

Pergunte ao Mago #415

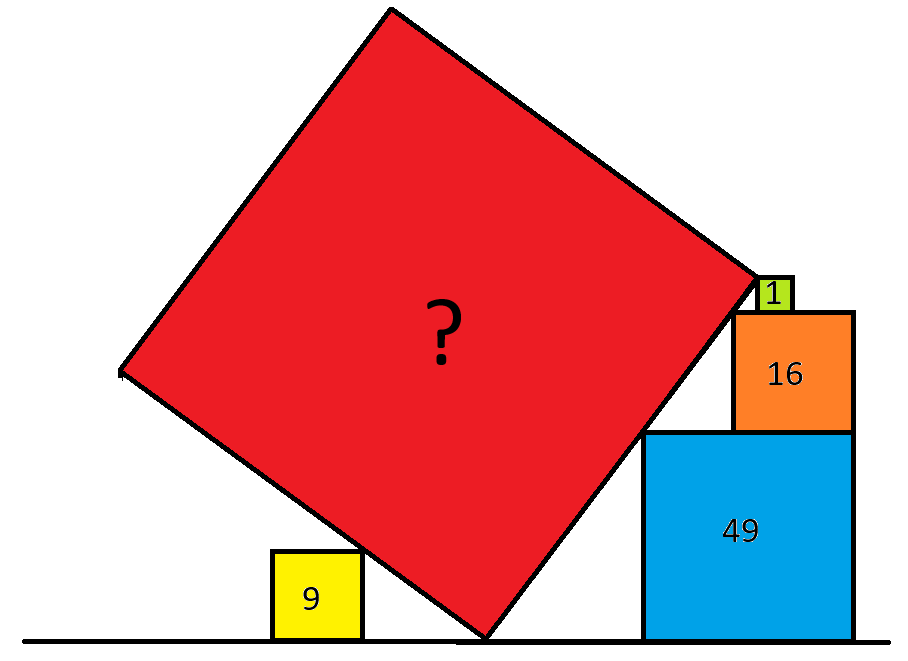
Na imagem acima, os números representam as áreas dos quatro quadrados. Qual é a área do quadrado vermelho?

anônimo

225

Primeiro, o quadrado amarelo não nos ajuda em nada. É uma pista falsa, então vamos ignorá-lo.

Em seguida, observe o triângulo à esquerda do quadrado laranja, conforme mostrado na imagem a seguir.

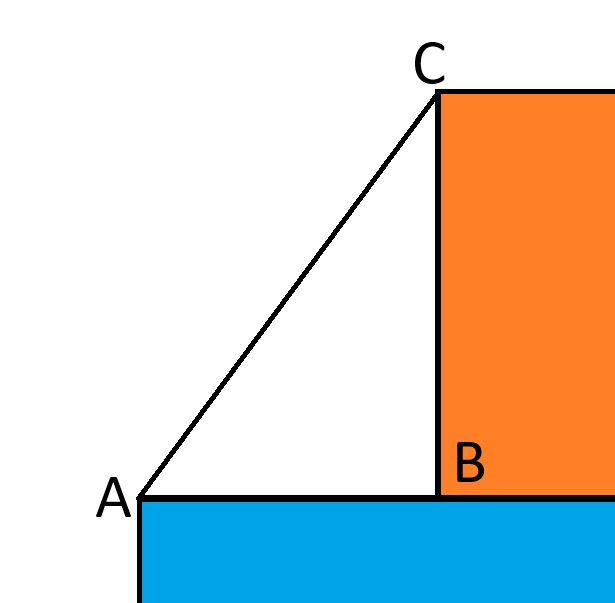
BC = sqrt(16) = 4.

AB = quadrado(49) - quadrado(16) = 7-4 = 3.

Pela fórmula de Pitágoras, AC² = 4² + 3² = 25.

AC = sqrt(25) = 5.

A altura de todos os três quadrados à direita é sqrt(49) + sqrt(16) + sqrt(1) = 12.

A razão entre o comprimento do lado do quadrado vermelho e a altura dos três quadrados à direita será a mesma que a razão entre AC e BC = 5/4.

Portanto, o comprimento do lado do quadrado vermelho é (5/4)*12 = 15.

Assim, a área do quadrado vermelho é 15 2 = 225.

Uma questão semelhante é apresentada e discutida no meu fórum, Wizard of Vegas .

O canal do YouTube Mind Your Decisions também tem um quebra-cabeça semelhante.

Qual é o menor retângulo possível cuja área é igual ao perímetro?

anônimo

As dimensões do retângulo são 4x4, resultando em uma área e perímetro de 16.

Sejam x e y as dimensões do retângulo.

Nos foi dado: xy = 2x + 2y.
2y - xy = 2x
y(2-x) = 2x
y=2x/(2-x)

Seja f(x) = A área do retângulo = x*y =
x*2x/(2-x) = 2x² /(2-x)

Para encontrar a área mínima, calcule a derivada usando a Regra do Quociente:

f'(x) = 4x(2-x) + 2x² / (2-x) ² = 0

4x(2-x) + 2x² = 0

8x = 2x²

x=4

Se x=4, y = 2*4/(4-2) = 8/2 = 4.

Vamos resolver para y para outros valores de x próximos de 4.

Se x=3, y=6 para uma área de 18

Se x=5, y = 10/3 para uma área de 16+(2/3).

É fácil ver que a solução em x=4 e y=4 resulta em um mínimo. Portanto, o menor retângulo possível é 4x4 = 16.

Em um sorteio de cassino, o número de bilhetes no tambor é o seguinte para cada portador:

  • O jogador 1 possui 6 bilhetes.
  • O jogador 2 possui 2 ingressos.
  • O jogador 3 possui 1 ingresso.
  • Outros 21 jogadores possuem 21 ingressos.

O cassino sorteará cinco bilhetes para cinco prêmios iguais. Cada jogador só pode ganhar uma vez. Se um bilhete for sorteado por um jogador que já ganhou, esse bilhete será descartado e um novo será sorteado.

Os jogadores 1, 2 e 3 concordam em dividir os ganhos de acordo com a sua participação no sorteio. Qual seria uma divisão justa?

Mukke

Vou simplificar o problema assumindo que, se um bilhete for sorteado por um jogador que já ganhou, esse prêmio será anulado. Caso contrário, os cálculos ficam muito complexos, praticamente exigindo uma simulação aleatória.

A probabilidade de um jogador que possui n bilhetes NÃO ganhar um prêmio é combin(30-n,5)/combin(30,n).

Assim, a probabilidade de o jogador A ganhar um prêmio é 1-combin(24,5)/combin(30,5) = 0,701739.

Assim, a probabilidade de o jogador B ganhar um prêmio é 1-combin(28,5)/combin(30,5) = 0,310345.

Assim, a probabilidade de o jogador C ganhar um prêmio é 1-combin(29,5)/combin(30,5) = 0,166667.

A soma dessas probabilidades é 1,178750. Esse é o número de vitórias que o grupo pode esperar obter.

Na minha opinião, cada jogador deveria receber uma parte igual à sua probabilidade de ganhar um prêmio dividida pelo total esperado de vitórias do grupo.

A recebe uma parte de 0,701739/1,178750 = 0,595324.

B recebe uma parte de 0,310345/1,178750 = 0,263283.

C recebe uma parte de 0,166667/1,178750 = 0,141393.

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .