Pergunte ao Mago #417
Sei que você era atuário do governo. Dito isso, os números desta tabela que supostamente mostram as tarifas cobradas sobre as importações para os Estados Unidos e as exportações de produtos americanos estão corretos?

Não.
Eu estava curioso sobre a origem dessas estatísticas. Começando pela coluna de tarifas cobradas dos EUA, descobri que elas não se referem a tarifas, mas sim ao déficit comercial. A tabela a seguir mostra o valor das importações e exportações para os EUA dos dez principais países da lista em 2024. A coluna "índice de déficit comercial" representa a razão entre as importações menos as exportações e as importações. Os valores de importação e exportação são apresentados em milhões de dólares. Observe que coincidem exatamente com os números da tabela que Trump tinha em mãos.
| País | Exportações | Importações | Troca Déficit Razão | "Tarifas Cobrado para os EUA" |
|---|---|---|---|---|
| China | $ 143.546 | $ 438.947 | 67% | 67% |
| União Europeia | $ 370.189 | $ 605.760 | 39% | 39% |
| Vietnã | $ 13.098 | $ 136.561 | 90% | 90% |
| Taiwan | $ 42.337 | $ 116.264 | 64% | 64% |
| Japão | $ 79.741 | $ 148.209 | 46% | 46% |
| Índia | $ 41.753 | $ 87.416 | 52% | 52% |
| Coréia do Sul | $ 65.542 | $ 131.549 | 50% | 50% |
| Tailândia | $ 17.719 | $ 63.328 | 72% | 72% |
| Suíça | $ 24.962 | $ 63.425 | 61% | 61% |
| Indonésia | $ 10.202 | $ 28.085 | 64% | 64% |
Fonte de importações e exportações: Departamento do Censo dos Estados Unidos .
Assim, a coluna "Tarifas cobradas aos EUA" no gráfico do presidente não tem nada a ver com tarifas, mas simplesmente representa o déficit comercial como percentagem das importações.
"E quanto à coluna dourada 'Tarifas Recíprocas com Desconto dos EUA'?", você pode perguntar. Ela representa simplesmente o maior valor entre metade da coluna "Tarifas Cobradas" e 10%. Isso pode ser verificado consultando a tabela.
Isso só demonstra que o simples fato de alguém apresentar uma grande quantidade de números e estatísticas não significa que essa pessoa esteja falando a verdade. Aliás, é um método comum de enganar as pessoas: bombardeá-las com números como se fossem uma mangueira de incêndio, na esperança de que o ouvinte seja preguiçoso demais para verificar os fatos. Não via um uso tão flagrante de estatísticas desde aquele vídeo sobre o debate homem versus urso . Na verdade, esta tabela de "Tarifas Recíprocas" é ainda pior.
Suponha que eu aposte $100 em um jogo de blackjack com baralho infinito e receba um par de dois contra um três do dealer. É permitido dobrar após dividir e o jogador pode dividir novamente infinitamente. Qual é a aposta total final esperada, assumindo que eu divida novamente o máximo possível e dobre se tiver um total de duas cartas de 9 a 11?
Vamos primeiro calcular quantas mãos você pode esperar obter após uma nova divisão. Seja n o número de mãos que uma única carta resultará após a nova divisão.
n=(12/13)×1 + (1/13)×2n
13n = 12 + 2n
11n = 12
n = 12/11 =~ 1,090909...
Com dois dois iniciais, o jogador pode esperar dividir novamente para 2×(12/11) = 24/11 =~ 2,181818 mãos.
A probabilidade de tirar um 7 a um 9 para quaisquer dois dados é 3 × (1/12) = 3/12 = 1/4. Estou dividindo por 12 e não por 13 porque, se o jogador tirasse um 2, ele dividiria o par novamente. Portanto, a média de unidades apostadas por mão após a divisão é (3/4) × 1 + (1/4) × 2 = 5/4 = 1,25.
Com uma aposta base de $100, a aposta final média é de $100×(24/11)×(5/4) = $272,73.
Essa pergunta foi feita e discutida no meu fórum no Wizard of Vegas .
Suponha que dois jogadores desejem jogar roleta russa de acordo com as seguintes regras.
- A arma é um revólver com seis câmaras.
- Para cada acionamento do gatilho, é necessário colocar de uma a cinco balas nas câmaras.
- O número de balas na arma pode mudar antes de cada disparo.
- A arma deve ser passada para frente e para trás após cada disparo.
- Nenhum outro método de randomização pode ser usado além da arma.
Qual é um método para garantir que cada jogador tenha 50% de chance de sobreviver?
A seguir, apresento apenas a minha resposta. Tenho certeza de que existem outras.
- Coloque duas balas na arma para o primeiro jogador. Se ele sobreviver, vá para o passo 2.
- Coloque três balas na arma para o segundo jogador. Se ele sobreviver, volte ao passo 1.
Se considerarmos p como a probabilidade de o jogador 1 perder, isso pode ser calculado da seguinte forma:
p = (2/6) + (4/6)*(3/6)p
36p = 12 + 12p
24p = 12
p = 12/24 = 1/2
Suponha que os lados de um quadrado de lado a sejam estendidos sobre uma linha abaixo do quadrado, criando distâncias de 2 e 5 sobre a linha.
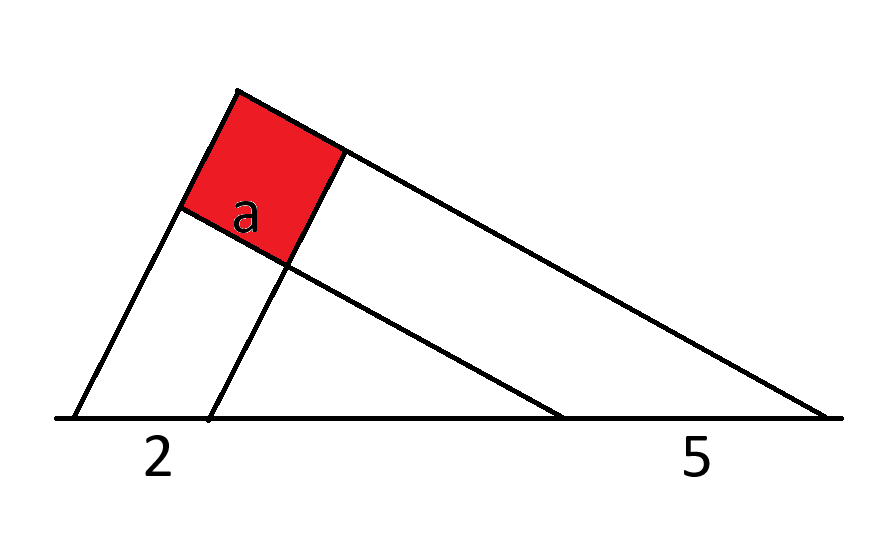
Qual é a área do quadrado?
Primeiro, vamos mover a linha para cima até que ela toque o canto do quadrado. Isso não afetará as distâncias na linha. Em seguida, vamos identificar os lados desconhecidos dos dois triângulos.
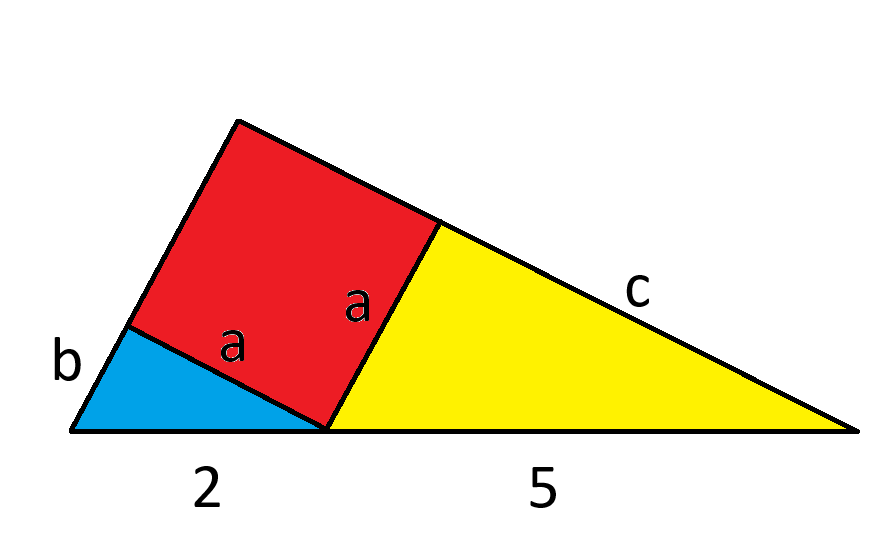
Os triângulos azuis e amarelos são triângulos retângulos.
Utilizando o teorema de Pitágoras no triângulo azul:
b² + a² = 4
b = sqrt(4-a 2 )
Usando o teorema de Pitágoras no triângulo amarelo:
c² + a² = 25
c = sqrt(25-a 2 )
Os triângulos azul e amarelo são semelhantes. Portanto, a razão entre a e b é igual à razão entre c e a:
a/√(4- a² ) = √(25- a² )/a
a 2 = sqrt(4-a 2 ) * sqrt(25-a 2 )
Elevando ambos os lados ao quadrado:
a 4 = (4 - a 2 ) * (25 - a 2 )
Seja x = a 2
x² = (4-x)(25-x)
x² = 100 - 29x + x²
29x = 100
x = 100/29
a = sqrt(x) = sqrt(100/29)
A pergunta pedia a área do quadrado vermelho, que é 2 = (sqrt(100/29)) 2 = 100/29.


