WOO logo

Recomendações do Mago

Pergunte ao Mago #418


Fonte da imagem: YouTube

A segunda temporada de The Squid Game apresenta um jogo chamado Pedra, Papel e Tesoura Menos Um, explicado neste vídeo . As regras são baseadas na versão clássica de Pedra, Papel e Tesoura, com estas modificações.

  • Ao mesmo tempo, ambos os jogadores jogam dois símbolos, um com cada mão.
  • Após examinarem o que foi lançado, na contagem de três, cada jogador recolhe um símbolo da mão que possui, deixando a outra mão vazia.
  • O jogo é pontuado de acordo com as regras padrão: pedra vence tesoura, papel vence pedra, tesoura vence papel.

O recrutador no vídeo do YouTube usa a seguinte situação como exemplo:

  • Triângulo brinca de tesoura e papel.
  • O grupo joga pedra e papel.

O recrutador diz que Triângulo deveria jogar papel, pois não tem como perder. Essa estratégia está correta? Acredito que Círculo provavelmente preveria essa estratégia e tentaria o empate jogando papel também. Portanto, talvez Triângulo devesse ao menos considerar arriscar e jogar tesoura. Qual é a estratégia ideal para ambos os jogadores?

anônimo

Após alguns cálculos, descobri que a estratégia ideal para ambos os lados é a seguinte:

  • Triângulo: Papel com probabilidade 2/3, tesoura com 1/3.
  • Círculo: Papel com probabilidade 2/3, pedra com 1/3.

Se pelo menos um jogador seguir essa estratégia, a probabilidade de cada resultado para o jogo Triângulo será a seguinte:

  • Vitória = 4/9
  • Empate = 4/9
  • Perda = 1/9

Para o Círculo, é o oposto, como segue:

  • Vitória = 1/9
  • Empate = 4/9
  • Perda = 4/9

Em resumo, o recrutador está completamente errado em seu conselho. Aqui está meu conselho geral para qualquer situação:

  • Comece sempre com dois símbolos diferentes.
  • Se você jogar os mesmos dois símbolos que seu oponente, jogue o símbolo que venceria o outro símbolo que você jogou. Por exemplo, se ambos jogarem pedra e papel, então jogue papel.
  • Se ambos os jogadores tiverem um símbolo em comum, então ambos os lados devem jogar esse símbolo em comum com probabilidade 2/3 e o outro com probabilidade 1/3.

Ligações

Qual é o número esperado de lançamentos necessários para obter o mesmo lado duas vezes em um dado de seis lados? E quanto a outros sólidos platônicos? Existe uma fórmula para qualquer dado de n lados?

anônimo

A resposta para um dado de seis lados é 1223/324 ≈ 3,774691 lançamentos.

A tabela a seguir mostra a resposta para vários números de lados.

Lados Esperado
Rolls
4 3,218750
6 3,774691
8 4,245018
12 5.036074
20 6,293585
50 9,543127
100 13.209961
200 18,398444

Aqui está uma fórmula para um dado de seis lados. Para qualquer outro tipo de dado, substitua o 6 pelo número de lados desejado.

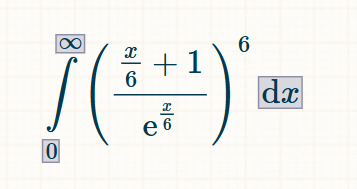
Para resolver integrais tão difíceis, recomendo o site integral-calculator.com .

Meus agradecimentos ao membro Ace2 do Wizard of Vegas pela ajuda com esta questão.

Suponha que você tenha a oportunidade de jogar um dado até que ele caia no número 6. Você ganhará o quadrado, em dólares, correspondente ao número de lançamentos necessários. Por exemplo, se forem necessários 6 lançamentos, você ganhará $25. Qual é o ganho esperado neste jogo?

anônimo

$66

Aqui está minha solução (PDF).