Pergunte ao Mago #419
Notei que você não tem nenhuma estratégia para vídeo poker com um pagamento maior para um royal flush sequencial. Você poderia me ajudar com isso?
Primeiramente, permita-me esclarecer alguns termos relacionados ao video poker.
- Sequencial Real = Apenas do mais baixo para o mais alto (10-JQKA)
- Real Reversível = Ambas as direções (10-JQKA ou AKQJ-10)
Para complicar ainda mais as coisas, nem todos usam essa terminologia, e um jogo que tem um item separado para um royal flush sequencial pode pagar das duas maneiras. Esperamos que as telas de regras esclareçam isso.
Dito isso, a maneira mais fácil e perfeita de jogar uma mão que pode ter um Royal Flush sequencial ou reversível é inseri-la na minha calculadora de vídeo pôquer. Aqui estão os links:
Se você não puder ou não quiser usar meu site na máquina, observe aqui os ganhos médios para um Royal Flush, quando um Royal Flush reversível paga 50.000 para uma aposta de 5 créditos, de acordo com quantas cartas já estão em posição.
- 4 para um real reversível = 10.000
- 3 para um real reversível = 5.400
- 2 para um real reversível = 2.333
- 1 para um real reversível (posição intermediária) = 1.567
- 1 para uma posição real reversível (não intermediária) = 1.183
- 0 a um real reversível = 800
Para jogos reais sequenciais (que pagam apenas do menor para o maior valor), use o valor 1.183, independentemente da posição.
Com esses dados, use meu criador de estratégias de vídeo pôquer e crie uma estratégia separada para cada uma dessas médias de vitórias com Royal Flush. Em seguida, use a estratégia na máquina de acordo com quantas cartas faltam para o Royal Flush estarem na posição correta.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
A Kellogg's lançou novas versões esféricas de Apple Jacks, Frosted Flakes e Krave, alegando que o formato proporciona mais cobertura. Na verdade, eles dizem: "Fizemos as contas". Será que fizeram corretamente?

Não!!!!!!!! Não, eles não fizeram os cálculos corretamente. Na verdade, a esfera é a PIOR forma tridimensional se o objetivo é maximizar a relação entre área de superfície e volume.
Vamos começar analisando as equações da área da superfície que estão no verso da caixa.

Eles afirmam corretamente que a área da superfície de uma esfera, ou o que provavelmente chamariam de buraco de rosquinha, é 4πr² , onde r = raio.
No entanto, eles afirmam incorretamente que a área da superfície de um toro, que provavelmente chamariam de rosca, é 2π²rR . A fórmula correta é o dobro disso, ou seja, 4π²rR . Consulte a imagem a seguir para ver os valores de r e R.
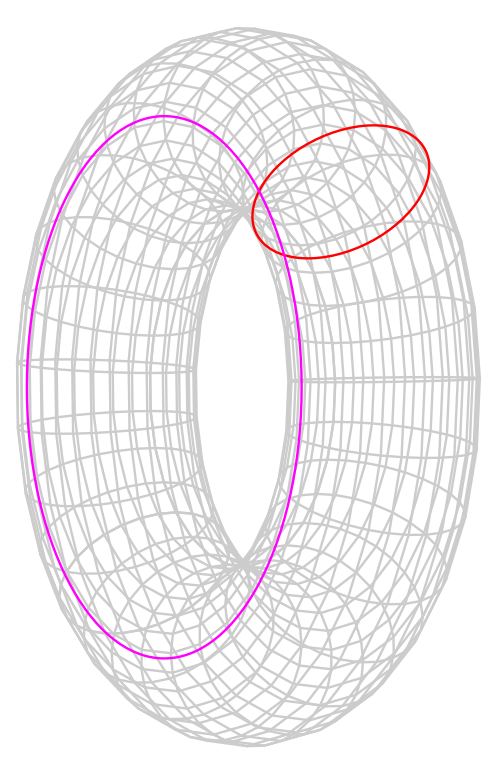
r = raio do círculo vermelho
R = distância da parte mais próxima do toro ao centro.
Fonte da imagem: Página da Wikipédia sobre o toroide .
Você pode argumentar que a alternativa a uma esfera seria aplicar glacê apenas em metade do toroide, como se faz com a cobertura de um donut. No entanto, uma análise cuidadosa dos tradicionais Apple Jacks em formato de toroide revela que o glacê é aplicado em toda a sua extensão.
Para ilustrar meu próximo ponto, permita-me também fornecer as fórmulas para o volume de uma esfera e de um toroide.
- Esfera = (4/3) πr³
- Toro = 2π 2 r 2 R
Só para lembrar, a fórmula para a área da superfície é a derivada do volume.
Para um toro de r=1 e R=1, obtemos uma área de superfície de 39,478418 e um volume de 19,739209. A razão entre a área da superfície e o volume, ou a razão do esmalte, é curiosamente exatamente 2.
Para igualar o volume, o raio de uma esfera teria que ser 1,676539. Para esse raio de esfera, obtemos uma área de superfície de 35,321350 e um volume de 19,739209. A razão entre a área da superfície e o volume, ou a razão do esmalte, é 1,789400.
Em outras palavras, o toroide proporciona uma área de superfície ou esmalte maior para o mesmo volume.
Mencionei anteriormente que a esfera é a pior forma tridimensional para se escolher quando o objetivo é maximizar a relação entre área de superfície e volume. Isso é conhecido como desigualdade isoperimétrica . Embora isso já tenha sido comprovado, acredito que seja autoevidente. Por exemplo, as bolhas tendem a minimizar a área de superfície e maximizar a resistência, e por isso têm formato esférico.
Resumindo, se você quer minimizar a quantidade de cobertura, e não aumentá-la, o ideal é escolher a versão esférica ou em formato de rosquinha do Apple Jacks, ou de qualquer outro cereal. Esse seria o meu objetivo, já que acho esses cereais doces demais e prefiro menos cobertura. Além disso, critico veementemente a Kellogg's por propaganda enganosa, o que lhes rende uma rara e lamentável reprimenda.
Essa pergunta é feita e discutida no meu fórum Wizard of Vegas .
Para mais informações, recomendo o vídeo "Internet spots big mistake on Kellogg's cereal box" (Internet aponta grande erro na caixa de cereal da Kellogg's) , do Presh Talwalkar, do canal MindYourDecisions (um dos meus favoritos!).
Qual a probabilidade de se obter uma mão vencedora no vídeo poker?
Consigo perceber como a resposta a esta pergunta teria aplicação prática em algumas variantes de video poker que oferecem um bónus caso o jogador consiga uma mão vencedora na distribuição das cartas.
A resposta depende do formato do video poker. A tabela a seguir mostra o número de combinações e a probabilidade de todos os eventos possíveis na distribuição das cartas no video poker com um baralho de 52 cartas sem curingas, começando com a mão de menor valor, um par de valetes.
| Mão | Combinações | Probabilidade |
|---|---|---|
| Rubor Real | 4 | 0,000002 |
| Straight flush | 36 | 0,000014 |
| Quatro de um mesmo tipo | 624 | 0,000240 |
| Casa cheia | 3.744 | 0,001441 |
| Descarga | 5.108 | 0,001965 |
| Direto | 10.200 | 0,003925 |
| Três de um tipo | 54.912 | 0,021128 |
| Dois pares | 123.552 | 0,047539 |
| Valetes ou melhor | 337.920 | 0,130021 |
| Todos os outros | 2.062.860 | 0,793725 |
| Total | 2.598.960 | 1.000000 |
A probabilidade de qualquer mão vencedora em jogos de video poker como Jacks or Better é de 0,206275.
A segunda tabela mostra o número de combinações e a probabilidade de todos os eventos possíveis na distribuição de cartas no vídeo pôquer com um baralho de 52 cartas, onde o dois é curinga, começando com a mão de menor valor, que é uma trinca.
| Mão | Combinações | Probabilidade |
|---|---|---|
| sequência real natural | 4 | 0,000002 |
| Quatro dois | 48 | 0,000018 |
| sequência real selvagem | 480 | 0,000185 |
| Cinco de um tipo | 624 | 0,000240 |
| Straight Flush | 2.068 | 0,000796 |
| Quatro de um tipo | 31.552 | 0,012140 |
| Casa cheia | 12.672 | 0,004876 |
| Descarga | 14.472 | 0,005568 |
| Direto | 62.232 | 0,023945 |
| Três de um tipo | 355.080 | 0,136624 |
| Todos os outros | 2.119.728 | 0,815606 |
| Total | 2.598.960 | 1.000000 |
A probabilidade de qualquer mão vencedora em jogos de video poker Deuces Wild é de 0,184394.
A terceira tabela mostra o número de combinações e a probabilidade de todos os eventos possíveis na distribuição das cartas no vídeo poker com um baralho de 53 cartas, incluindo um curinga, começando com a mão de menor valor, um par de reis.
| Mão | Combinações | Probabilidade |
|---|---|---|
| cinco de um tipo | 13 | 0,000005 |
| Rubor Real | 24 | 0,000008 |
| sequência de naipes | 180 | 0,000063 |
| quatro de um tipo | 3.120 | 0,001087 |
| Casa cheia | 6.552 | 0,002283 |
| descarga | 7.804 | 0,002719 |
| direto | 20.532 | 0,007155 |
| 3 de um tipo | 137.280 | 0,047838 |
| 2 pares | 123.552 | 0,043054 |
| Reis ou melhor | 262.956 | 0,091632 |
| Todos os outros | 2.307.672 | 0,804155 |
| Total | 2.869.685 | 1.000000 |
A probabilidade de qualquer mão vencedora em jogos de video poker com joker poker (reis ou melhor) é de 0,195845.


