WOO logo

Recomendações do Mago

Pergunte ao Mago #422

Para fins de argumentação, supondo um jogo de blackjack com um número infinito de baralhos, onde o re-splitamento é permitido infinitamente e o jogador dividirá qualquer par, qual é a probabilidade de qualquer número dado de mãos finais que o jogador jogar?

anônimo

A probabilidade de dividir novamente em n mãos é (combin(2*(n-1),n-1)/n) × (1/13)^(n-1) × (12/13)^n . Para mais informações sobre esse primeiro termo, com o qual precisei de ajuda, pesquise sobre números catalães .

A tabela a seguir mostra a probabilidade de 1 a 20 mãos finais. A coluna dos segundos indica o número de "árvores", que é o número catalão na expressão acima.

Mãos Árvores Probabilidade
1 1 0,9230769230769
2 1 0,0655439235321
3 2 0,0093080128093
4 5 0,0016523099661
5 14 0,0003285065968
6 42 0,0000699777366
7 132 0,0000156163334
8 429 0,0000036037693
9 1430 0,0000008529631
10 4862 0,0000002059225
11 16796 0,0000000505114
12 58786 0,0000000125531
13 208012 0,0000000031540
14 742900 0,0000000007998
15 2674440 0,0000000002045
16 9694845 0,0000000000526
17 35357670 0,0000000000136
18 129644790 0,0000000000035
19 477638700 0,0000000000009
20 1767263190 0,0000000000002

Ouvi dizer que existem infinitos ternos pitagóricos. Existe alguma fórmula para encontrá-los?

anônimo

Sim, existem infinitos ternos pitagóricos únicos! Para quem não está familiarizado com o termo, são triângulos retângulos onde cada lado é um número inteiro. O 3-4-5 é o mais famoso. Para obter um terno pitagórico único (ou seja, não redutível), escolha quaisquer valores inteiros para a e b, onde a < b e um seja ímpar e o outro par.

  • Perna 1 = b 2 - a 2
  • Perna 2 = 2ab
  • Hipotenusa = a² + b²

A tabela a seguir mostra todos os ternos pitagóricos irredutíveis em que todos os lados medem 101 ou menos.

a,b Etapa 1 Etapa 2 Hipotenusa
1,2 3 4 5
1,4 8 15 17
1,6 12 35 37
1,8 16 63 65
1,10 20 99 101
2,3 5 12 13
2,5 20 21 29
2,7 28 45 53
2,9 36 77 85
3,4 7 24 25
3,6 27 36 45
3,8 48 55 73
4,5 9 40 41
4,7 33 56 65
4,9 65 72 97
5,6 11 60 61
5,8 39 80 89
6,7 13 84 85

Qual é a probabilidade de se obter, com dois dados, pelo menos duas vezes qualquer total diferente de sete antes de se obter um sete?

Garrison

O truque para resolver questões como essa é que a probabilidade é a mesma se o intervalo de tempo entre os lançamentos seguir uma distribuição exponencial com média igual a 1. Nesse caso, ela pode ser expressa pela seguinte fórmula.

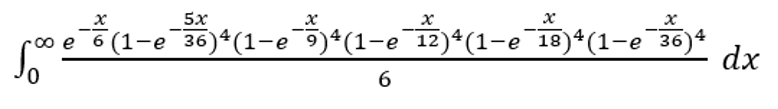
Para escrever em formato de texto: exp(-x/6)*(1-exp(-5x/36))^4*(1-exp(-4x/36))^4*(1-exp(-3x/36))^4*(1-exp(-2x/36))^4*(1-exp(-1x/36))^4/6

Para resolver essas integrais, recomendo esta Calculadora de Integrais .

A resposta é 7864581698887803455719/10946915593544650625105200 =~ 0,0007184290069364848.