Pergunte ao Mago #426
Suponha que os números de série sejam numerados sequencialmente a partir de 1. O número máximo em circulação é desconhecido. Dada uma amostra aleatória de n números, qual é a melhor estimativa do número de série máximo?
A maneira que eu gosto de pensar para encontrar a resposta é calcular a distância média entre os números de série. Para isso, pegue o valor máximo e divida pelo tamanho da amostra. Por exemplo, se o maior item da sua amostra for 1.000 e você tiver um tamanho de amostra de 5, então a distância média será 1.000/5 = 200. Em seguida, adicione essa distância à observação máxima para obter o número máximo estimado. Neste exemplo, 1.000 + 200 = 1.200.
A fórmula usual que chega ao mesmo número é M*(k+1)/k, onde M = valor máximo e k = número de observações. No nosso exemplo, isso resulta em 1000*(6/5) = 1200.
ABCD é um quadrado com lado de comprimento 10. Em seu interior estão inscritos um semicírculo e um quarto de círculo, conforme mostrado no diagrama a seguir.
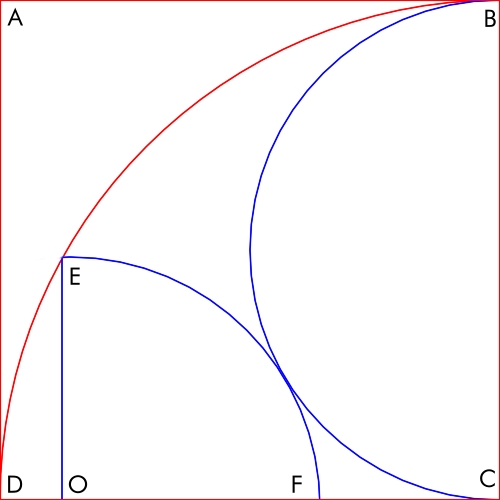
Qual é a duração de OE?
Considere o seguinte diagrama.
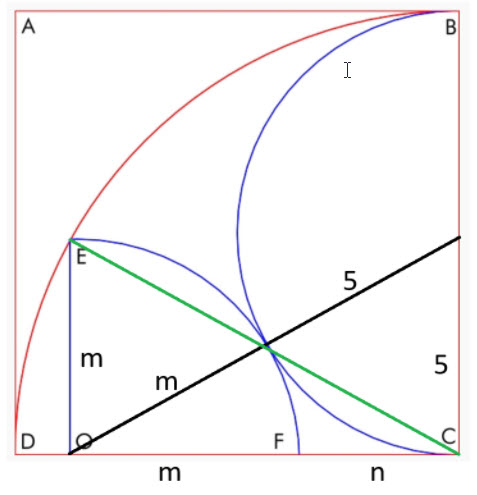
Aqui temos dois triângulos retângulos, um com a hipotenusa verde e o outro com a hipotenusa preta. Vamos montar as duas equações pitagóricas:
- Hipotenusa verde: m² + (m+n) ² = 10²
- Hipotenusa preta: 5² + (m+n) ² = (m+5) ²
Vamos rearranjar a primeira equação para (m+n) ² = 10² - m²
Vamos substituir esse valor de (m+n) ² na segunda equação:
5² + 10² - m² = (m+5) ²
25 + 100 - m² = m² + 10m + 25
2m² + 10m - 100 = 0
m² + 5m - 50 = 0
Utilizando a fórmula de Pitágoras para resolver para m:
m = (-5 +/- sqrt(25 + 200))/2
m = 5 ou -10. 5 é a única resposta razoável.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Um grande número de alunos está fazendo uma prova de 10 questões. Cada questão é de verdadeiro ou falso. Qual é o número máximo de alunos que podem fazer a prova de forma que quaisquer duas provas difiram entre si em pelo menos duas questões?
[spoiler=Solução]
Faça um teste específico, que chamaremos de teste principal.
Grupo 1 = O número de maneiras pelas quais outros testes podem ser diferentes em exatamente 2 questões do teste chave é combin(10,2)=45.
Não vou calcular o número de maneiras de diferir em 3 em relação ao teste principal, porque algumas dessas maneiras corresponderão 9 em cada 10 a um teste do grupo 1.
Grupo 2 = O número de maneiras pelas quais outros testes podem ser diferentes em exatamente 4 questões do teste principal é combin(10,4)=210. Qualquer um deles também diferirá de qualquer teste no grupo 1 em pelo menos 2.
Repetindo essa lógica...
- Grupo 3 = O número de maneiras pelas quais outros testes podem ser diferentes em exatamente 6 questões do teste chave é combin(10,6)=210.
- Grupo 4 = O número de maneiras pelas quais outros testes podem ser diferentes em exatamente 8 questões do teste chave é combin(10,8)=45.
- Grupo 5 = O número de maneiras pelas quais outros testes podem ser diferentes em exatamente 10 questões do teste chave é combin(10,10)=1.
Portanto, a resposta é a soma dos grupos 1 a 5 mais um para o teste chave = 1+45+210+210+45+1 = 512.
Esse número é o mesmo que 2^9. Será coincidência? Não!
O número de maneiras de retirar um número ímpar de itens de um grupo maior é o mesmo que o número de maneiras de retirar um número par. Isso ocorre porque cada item no grupo maior pode ser escolhido ou não escolhido. Existem 2^n combinações de cada membro sendo escolhido ou não escolhido em um grupo de n itens. Se você os listasse sistematicamente em ordem binária, o número de combinações escolhidas alternaria entre par e ímpar. O número total de itens no grupo é 2^n, que é par, portanto, metade de 2^n será par.
Portanto, a soma dos grupos de 1 a 5 é o número de maneiras de escolher um número par de questões que correspondam ao gabarito. Isso será igual ao número de maneiras de escolher um número ímpar de questões que correspondam ao gabarito. O número total de maneiras de corresponder ou não ao gabarito é 2^10 = 1024. Metade dessas corresponderá um número par de vezes. Portanto, a resposta é 1024/2 = 512.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .


