Recomendações do Mago
-
Bônus de boas-vindas de $11000 -
Bônus de boas-vindas de 3000 $ -
BÔNUS DE ATÉ $777
Pergunte ao Mago #427
Um bolo é dividido da seguinte forma:
- A primeira pessoa ganha 1%
- A segunda pessoa fica com 2% do que sobrar.
- A terceira pessoa fica com 3% do que sobrar.
- E assim por diante.
Quem vai ganhar mais bolo? Sem planilhas ou cálculos por força bruta.
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Gostaria de dar os créditos ao canal do YouTube Mind Your Decisions por este quebra-cabeça matemático.
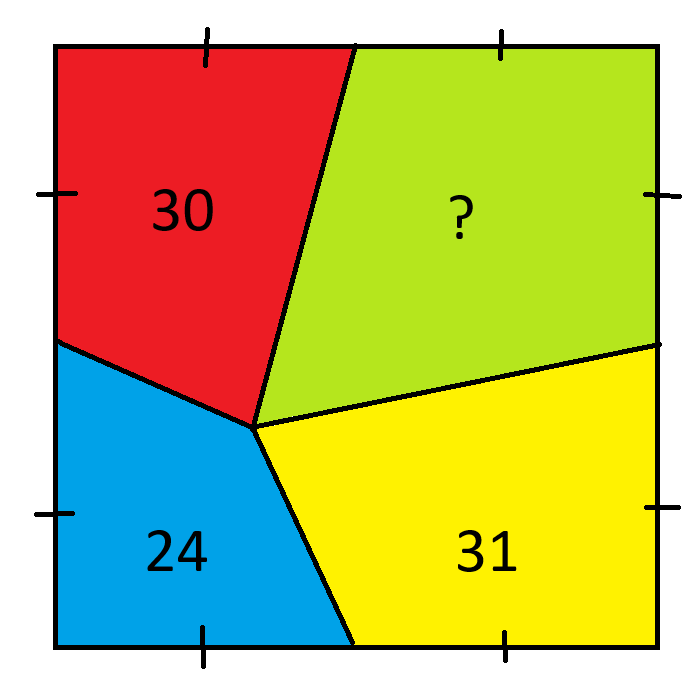
Qual é a área da região verde?
Primeiro, trace quatro linhas da interseção das quatro peças até cada canto. Em seguida, identifique as oito peças da seguinte forma.
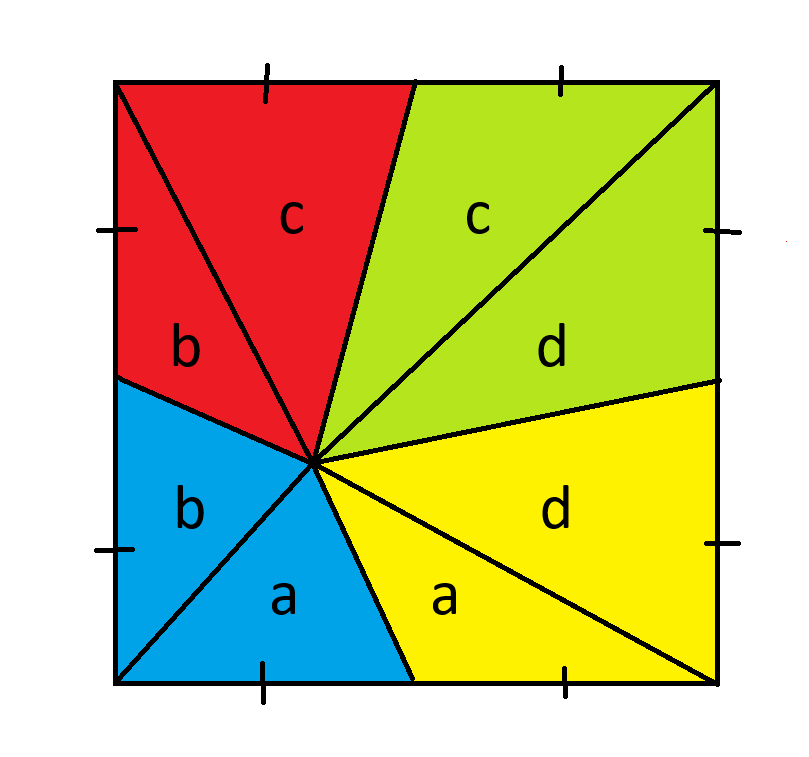
Lembre-se que a área de um triângulo é base * altura / 2. Como todos os triângulos têm a mesma base, podemos considerar que triângulos com a mesma altura têm a mesma área.
Neste momento sabemos:
- (1) A+B = 34
- (2) B+C = 42
- (3) A+D = 30
Somando as equações (2) e (3):
A+B+C+D = 72
Vamos subtrair a equação (1) disso:
C+D = 38, que é a nossa resposta.
Essa pergunta foi feita e discutida no meu fórum no Wizard of Vegas .
A origem do enigma é o vídeo do YouTube intitulado "98% FALHOU em resolver este problema de matemática".
Digamos que você queira encontrar a média de vários valores. Qual a sua opinião sobre descartar os valores mais altos e mais baixos, como acontece na pontuação da ginástica olímpica? Digamos que o objetivo seja encontrar o valor médio por metro quadrado de um determinado bairro.
Boa pergunta. O que você está descrevendo é chamado de média aparada. Não conheço nenhuma estatística para a variância da média aparada em relação à média verdadeira. Na falta de uma ideia melhor, fiz meu próprio experimento.
Para responder à sua pergunta, coletei 100.000 amostras de dez conjuntos de valores. Cada valor foi distribuído de acordo com a distribuição normal padrão, ou seja, com média 0 e variância 1. Em seguida, analisei a média de todos os dez valores, bem como a média dos oito valores descartados.
O que descobri foi que a diferença média entre a média da amostra e a média real, considerando todos os dez valores, foi de 0,003450. Fazendo o mesmo, mas calculando a média da média aparada, a diferença média foi de 0,003445. Na minha opinião, essa diferença não é significativa o suficiente para afirmar qual método é melhor. Além disso, o que pode ser adequado para o meu experimento pode não ser para outra aplicação.
Em conclusão, e não costumo dizer isso, não tenho uma resposta matemática definitiva.
Qual é a maneira mais eficiente (ou seja, que ocupa menos espaço) de empilhar esferas, com base quadrada ou triangular?
A forma como respondi foi determinando qual pirâmide apresentava a maior proporção entre o volume das esferas e o volume da pirâmide que as envolvia, à medida que o número de esferas se aproximava do infinito.
Aqui está minha solução (PDF).
Mais tarde, percebi que essa pergunta também foi feita em Ask the Wizard #350 . No entanto, acho que esta solução é melhor.