Blackjack - Perguntas gerais
Existem cassinos em Las Vegas além do Mandalay Bay onde o dealer para no 17 suave? Joguei uma partida de Spanish 21 no MGM. Não vejo nenhuma vantagem em não ter os dez, especialmente em apostas duplas.
Pelo que sei, na grande maioria dos jogos de cartas com sapata em Las Vegas, o dealer para no 17 suave. Normalmente, o dealer pede carta no 17 suave em jogos com um baralho, enquanto em jogos com dois baralhos, a decisão pode ser tomada de ambas as maneiras. Tento explicar o porquê da contagem de cartas na minha página sobre o assunto .
Como a casa tem vantagem no Blackjack?
O crupiê tem a vantagem porque o jogador tem que começar. Se ambos ultrapassarem 280 pontos, não é um empate, mas VOCÊ perde.
Qual é a aposta mínima no blackjack na maioria dos cassinos online? Existe um limite de tempo para tomar decisões nas mesas de blackjack? Se sim, qual é?
O valor mínimo varia de cassino para cassino. Nos cassinos da Unified Gaming, é de US$ 1, na Microgaming é de US$ 2, e na Starnet e Cryptologic é de US$ 5. Se você estiver jogando sozinho, pode levar bastante tempo. Já aconteceu de eu receber ligações no meio de uma mão, voltar 15 minutos depois e continuar jogando sem ter sido desconectado. Você será desconectado por inatividade eventualmente, mas isso leva um bom tempo. No entanto, se estiver jogando em uma mesa com outros jogadores, há um limite de tempo por decisão de cerca de 30 segundos. No Sands of the Caribbean, você pode ver o tempo passando.
Como apostador iniciante em Las Vegas, me recomendaram jogar craps e Caribbean Stud. Quanto dinheiro devo levar para cada jogo para tentar permanecer na partida tempo suficiente para obter resultados?
Se você jogar por tempo suficiente, o único resultado que verá é a perda de todo o seu dinheiro. Não aposte mais dinheiro do que você está disposto a perder nessa sessão.
Em segundo lugar, o Caribbean Stud Poker tem uma vantagem da casa de 5,22%, então, se você está tentando permanecer no jogo o máximo de tempo possível, eu evitaria esse. Os melhores jogos de mesa são craps e blackjack, quando jogados corretamente.
Por que as tabelas de estratégia básica de blackjack são elaboradas com a aparente teoria de que o dealer tem um "10" na mão fechada? Quando, na realidade, acredito que as probabilidades são de 9 para 4 contra a presença de um "10" em qualquer mão. Estou perdendo alguma coisa? Seu site é muito interessante. Muito obrigado.
Presumir que o dealer tem um 10 na mão fechada é apenas um recurso de memorização, não tem nada a ver com a forma como a estratégia básica foi construída. Não consigo ficar de fora quando ouço um jogador dizer para o outro: "Você sempre presume que o dealer tem um 10 na mão fechada". Se isso fosse verdade, o jogador deveria pedir carta com um 19 contra um 10, o que certamente seria uma jogada irracional.
Entre as diversas estratégias de blackjack que vocês oferecem no site, o desvio padrão varia muito? Imagino que, quando o DAS é permitido, os resultados sejam mais variáveis, mas quanto? Existe algum bom livro de referência que forneça dados de variância para as diferentes estratégias básicas de blackjack?
Boa pergunta. Infelizmente, não tenho os valores exatos do desvio padrão de acordo com regras específicas. O valor de 1,15 no meu site é baseado nas regras mais flexíveis da Las Vegas Strip. Concordo que a regra de dobrar após dividir aumenta o desvio padrão. Desistir o diminuiria. Sinto muito por não poder ajudar mais do que isso.
Existe alguma prova matemática que você possa fornecer que demonstre que um jogador na "terceira base" da mesa de blackjack não pode alterar o resultado do jogo tomando decisões ruins baseadas em "estratégia básica"? Muitas pessoas argumentam que decisões ruins na terceira base, ou em qualquer outra posição na mesa, custam dinheiro a elas. Gostaria muito de ver os números que comprovam isso, se possível. Ótimo site, aliás. Adoro jogos de azar, e o seu site é um dos melhores que já vi na internet. Tem informações realmente comprovadas.
Obrigado pelas suas amáveis palavras. Infelizmente, não tenho nenhuma prova desse tipo em mãos. Se eu mesmo tentasse provar, usaria uma simulação por computador. No entanto, os céticos provavelmente alegariam algo absurdo, como o fato de que jogadores mal-intencionados perturbam o karma do jogo, algo que não pode ser replicado em um computador.
Será que o que eu observo tem mesmo fundamento estatístico? Parece-me que levo muito mais tempo para ganhar X fichas do que para perder a mesma quantia (jogo apenas blackjack). Por exemplo, se começo com 300 fichas, posso levar horas para dobrar meu dinheiro (meu objetivo), mas posso perder essa mesma quantia em um piscar de olhos. Isso é realmente possível? Além disso, existe alguma regra prática sobre quando sair da mesa quando estou ganhando?
O que você vivenciou provavelmente é resultado de uma sequência de derrotas muito ruins. Também pode ser consequência de apostas progressivas ou erros de estratégia. O jogador que adota a estratégia básica de apostar com uma mão fixa deve ter uma expectativa aproximadamente simétrica em termos de grandes altas e baixas, com uma ligeira vantagem para as grandes baixas devido à vantagem da casa e uma probabilidade de 48% de perder a mão, em comparação com 43% de ganhar. Se estou jogando por diversão, saio da mesa quando a diversão acaba.
Qual é o melhor jogo para o jogador: Spanish 21 ou blackjack tradicional em Atlantic City?
Spanish 21! De acordo com as regras de Atlantic City, o blackjack tem uma vantagem da casa de 0,43% e o Spanish 21 de 0,40%.
Você quer dizer que o homem criou uma maneira de colocar três milhões de transistores em um único chip (microprocessador) do tamanho de uma unha, e nós não temos como vencer uma aposta de 50/50? Acho isso inacreditável. Além disso, constatei que simulações por computador definitivamente não são a mesma coisa que a experiência real. E por que os cassinos não introduzem o blackjack eletrônico para acabar com os contadores de cartas e eliminar os crupiês?
Já afirmei diversas vezes que não existe uma maneira de vencer um jogo com vantagem da casa a longo prazo. Se existisse um jogo verdadeiramente equilibrado (50/50) sem vantagem da casa, seria impossível garantir a vitória ou a derrota em condições reais. Os resultados sempre se aproximam da vantagem da casa a longo prazo. Isso não se baseia apenas em simulações computacionais, mas sim nas leis fundamentais da probabilidade.
Sobre o blackjack em vídeo, esse pode ser o futuro. Vi mesas totalmente eletrônicas com tela de vídeo na World Gaming Expo. Também vi mesas com câmeras que rastreiam cada aposta e cada jogada de cada jogador. Isso permite que a casa ofereça bônus aos jogadores com precisão e os alerte sobre contadores de cartas. Essas mesas têm a mesma aparência e sensação de qualquer outra mesa de blackjack, então os contadores de cartas podem ficar sem emprego se essas mesas fizerem sucesso.
Qual o melhor lugar para jogar Blackjack em Atlantic City e por quê?
O Claridge é o melhor. Pelo que sei, é o único cassino de Atlantic City que oferece a opção de desistência tardia, o que reduz a vantagem da casa de 0,43% para 0,36%.
Sei que vocês listam a vantagem da casa no blackjack no site de vocês para quem joga com a estratégia básica, mas gostaria de saber qual é a vantagem média da casa contra um iniciante típico. Além disso, poderiam calcular qual a melhor vantagem que uma casa poderia ter sobre o pior jogador, considerando que ele nunca pediria carta acima de um 16 rígido? Agradeço desde já.
De acordo com o livro "Extra Stuff" de Peter Griffin, o custo devido a erros do jogador médio é de 1,41%. Isso é superior à vantagem da casa, considerando uma estratégia básica adequada. Também varia conforme o local; jogadores de Atlantic City, por exemplo, são melhores que os de Las Vegas. Sua outra pergunta sobre estratégias ruins foi tão boa que adicionei informações sobre o assunto à minha seção de blackjack. Veja meus comentários sobre estratégias ruins .
Primeiramente, acho seu site excelente e gostaria de agradecer por todas as informações valiosas e sólidas. Minha dúvida é a seguinte: as mesas de blackjack têm um limite máximo de aposta que aumenta consideravelmente quando se passa da mesa de cinco dólares para a de dez dólares, e assim por diante. Imagino que isso seja para desencorajar jogadores com apostas altas de jogarem em mesas com apostas mais baixas, mas como esses limites são calculados? Percebi que eles variam de cassino para cassino. Além disso, em seu gráfico sobre a vantagem da casa, seria ótimo ver uma comparação da vantagem da casa para um jogador de blackjack usando a Estratégia Básica versus um que conta cartas. Agradeço novamente pelo excelente trabalho.
De nada! Os cassinos geralmente tentam manter a aposta máxima entre 200 e 500 vezes a aposta mínima. Por quê? Se um cassino aceita uma aposta de US$ 10.000 em uma mesa de US$ 100, por que não aceitá-la em uma mesa de US$ 5? A resposta parece ser que os cassinos gostam de concentrar seus grandes apostadores em áreas específicas. Essas áreas de alto limite tendem a ter a melhor equipe e vigilância. Limitar a proporção entre a aposta máxima e a mínima também é uma forma de evitar trapaças e jogos de vantagem.
A vantagem da contagem de cartas depende da habilidade e agressividade do jogador. Além da minha introdução à contagem de cartas , deixo esse tópico para outros autores que escrevem sobre jogos de azar.
No jogo de blackjack, você poderia me dizer se a entrada e saída de jogadores altera as minhas chances de ganhar ou perder? Parece ter um efeito quando estou jogando.
Não, a entrada e saída de outros jogadores não terá efeito a longo prazo nas suas probabilidades. Isso pode parecer verdade, mas suspeito que você se lembre mais facilmente das vezes em que entradas e saídas te prejudicaram do que das vezes em que te ajudaram. No fim das contas, as cartas são as cartas e todos os outros fatores se anulam.
Gosto tanto de Caribbean Stud quanto de Blackjack. O elemento de risco no Stud é de 2,56% e no Blackjack é de 0,38%, ou seja, uma proporção de 6,7. Suponha que eu jogue Blackjack com uma aposta inicial de $15 e Stud com uma aposta inicial de $5, ou seja, $15 em risco a cada aposta. Como o número de mãos distribuídas por hora é muito maior no Blackjack do que no Stud, isso significa que perderei a mesma quantia da minha banca se a proporção de mãos distribuídas por hora for de 6,7?
Não. Se você estiver interessado em comparar as perdas esperadas, seria melhor usar a vantagem da casa. Minha seção sobre a vantagem da casa mostra que a vantagem da casa no blackjack é de 0,43% (regras de Atlantic City) e a do Caribbean Stud Poker é de 5,22%. A perda esperada para 1 mão de Caribbean Stud Poker com um ante de $5 é de $5 * 5,22% = 26,10 centavos. A perda esperada para 6,7 mãos de blackjack com uma aposta inicial de $15 é de 6,7 * $15 * 0,43% = 43,22 centavos. Portanto, considerando essas duas opções, você perderá menos no Caribbean Stud Poker. A proporção da vantagem da casa do Caribbean Stud Poker para o blackjack é de cerca de 12. Assim, a perda esperada de uma aposta inicial de $1 no Caribbean Stud Poker é aproximadamente a mesma que uma aposta inicial de $12 no blackjack.
Minha dúvida é sobre as apostas máximas na mesa de Blackjack. Digamos que o limite anunciado seja de $200. Eu aposto $200 e recebo 8-3. Posso dobrar a aposta ou já atingi o limite? Ou, suponha que eu aposte $200 e receba um par de ases. Posso dividi-los, transformando uma mão em duas?
Sim, você poderia dobrar ou dividir nessas situações. O limite máximo se aplica à aposta inicial. Se o limite fosse de $200, você também poderia jogar várias mãos de $200.
Meu amigo e eu temos uma aposta paralela. Eu disse a ele que acho que o blackjack tem as melhores probabilidades em um cassino, e ele me disse que acha que o pôquer tem as melhores probabilidades. Em um cassino, qual jogo oferece as melhores chances de ganhar: blackjack ou pôquer?
Embora seja difícil comparar, eu diria que o blackjack é a melhor opção. É fácil se tornar um bom jogador de blackjack aprendendo a estratégia básica. Já o pôquer, é difícil. As salas de pôquer dos cassinos costumam estar cheias de jogadores muito bons, só esperando para enganar um jogador inexperiente. No entanto, algumas pessoas podem ter um talento natural para o pôquer, então leve minha resposta com cautela.
No Blackjack, qual a diferença entre desistir antecipadamente e desistir tardiamente?
Na desistência antecipada, você pode desistir antes que o crupiê verifique se tem blackjack. Com a desistência tardia, você só tem essa opção depois que o crupiê verifica se tem blackjack. A desistência antecipada é muito melhor porque você ainda pode salvar metade da sua aposta caso o crupiê tenha blackjack. Até onde eu sei, nenhum cassino físico ou online oferece atualmente a opção de desistência antecipada.
Prezado Mago, só uma perguntinha rápida: por que a vantagem da casa muda em uma aposta de seguro no blackjack dependendo do número de baralhos usados?
Como já sabemos que um ás foi removido do sapato, o restante do sapato fica com uma ligeira predominância de dez. Quanto maior a proporção de dez no sapato, maior a probabilidade de a aposta de seguro ser vencedora. Quanto menos baralhos, maior será esse efeito. Fazer um seguro para um 20 (exceto A/9) aumenta a vantagem da casa na aposta de seguro porque há dois dez a menos no sapato.
Em resposta à sua última coluna, de um jogador preocupado com o fato de o crupiê ter anunciado "aposta máxima da mesa" quando ele aumentou sua aposta de $15 para $300, deve-se acrescentar à sua resposta que este é provavelmente o procedimento interno do cassino, já que a maioria age assim quando qualquer aposta máxima é feita, a fim de chamar a atenção do supervisor. Muitos jogadores tendem a acreditar que as ações de um cassino são direcionadas contra eles, quando, na realidade, o motivo é simplesmente que a equipe está seguindo os procedimentos da empresa.
Obrigado por essa observação pertinente. Corrigindo minha afirmação anterior.
Adoro seu site! Gosto de jogos de cassino, mas geralmente só posso jogar com uma banca pequena (menos de US$ 100 por sessão). Que jogo você recomendaria para maximizar o tempo de duração da minha banca e as chances de uma sessão vencedora?
Obrigado. Considerando as probabilidades de ganhar e a preservação da banca, acho que a escolha se resume a blackjack (que favorece as vitórias) e pai gow poker (que favorece a preservação da banca). Se você encontrar uma mesa de $5 em qualquer um dos jogos, eu escolheria o blackjack. Se o mínimo for $10, então eu escolheria o pai gow poker.
Ocasionalmente, jogo com um grupo de jogadores que adoram pôquer, mas que às vezes querem jogar Blackjack para variar a programação da noite. A maioria deles é iniciante em termos de estratégia e noção de probabilidades. Quais seriam regras justas que você recomendaria para que o Blackjack se torne um jogo justo (ou o mais próximo possível disso) tanto para os jogadores quanto para quem leva a banca?
Isso dependeria do nível de habilidade específico de cada jogador. Sem saber isso, mas assumindo que o nível de habilidade seja igual entre os jogadores, eu faria com que a opção de saque rotacionasse entre eles.
Sei que o número de decisões por hora em jogos como blackjack e craps pode variar bastante dependendo de fatores como a quantidade de outros jogadores na mesa, o embaralhamento manual versus o automático, a velocidade do lançador e do dealer. Mesmo assim, gostaria de saber se você poderia me dar uma estimativa aproximada de quantas decisões por hora um jogador pode esperar em uma mesa de craps quase cheia e em uma mesa de blackjack com embaralhamento manual e automático. Isso me ajudaria a estimar meu prejuízo esperado por hora e compará-lo com os benefícios que me estão sendo oferecidos.
As tabelas a seguir mostram o número de mãos/lançamentos por hora no blackjack, craps e roleta. A fonte das tabelas é o livro "Casino Operations Management" de Jim Kilby.
Mãos por hora no Blackjack
| Jogadores | Mãos por hora |
| 1 | 209 |
| 2 | 139 |
| 3 | 105 |
| 4 | 84 |
| 5 | 70 |
| 6 | 60 |
| 7 | 52 |
Lançamentos por hora no Craps
| Jogadores | Rolos por hora |
| 1 | 249 |
| 3 | 216 |
| 5 | 144 |
| 7 | 135 |
| 9 | 123 |
| 11 | 102 |
No jogo de dados, em média, 29,6% dos lançamentos totais são lançamentos "come out".
Giros por hora na roleta
| Jogadores | Rotações por hora |
| 1 | 112 |
| 2 | 76 |
| 3 | 60 |
| 4 | 55 |
| 5 | 48 |
| 6 | 35 |
Quanto tempo levaria para eu perder US$ 10.000 com apostas fixas de US$ 5 jogando blackjack de 6 baralhos no estilo Vegas Strip?
A perda esperada por mão seria de $5 * 0,0062 = 3,1 centavos, assumindo que você jogue a estratégia básica correta e que o dealer peça carta com um 17 suave, o que geralmente acontece em jogos de $5. Supondo que você perdesse exatamente esse valor por mão, seriam necessárias 322.580 mãos. No entanto, o número real seria um pouco menor devido à volatilidade da banca e ao fato de que você não pode jogar depois de ficar sem dinheiro. Para fazer uma estimativa fundamentada, eu diria cerca de 300.000 mãos. A 60 mãos por hora, isso daria 5.000 horas, ou dois anos e meio de jogo em tempo integral.
Ótimo site, continuem com o excelente trabalho. Estou procurando um jogo (ou jogos) que me permita recuperar uma unidade. Por exemplo, se eu apostar 10 dólares, gostaria de receber meus 10 dólares iniciais de volta, mais os 10 dólares que apostei. Acredito que a linha de passe do craps seja a melhor opção para isso. Não me importo de perder um pouco de dinheiro, se necessário, mas espero recuperar pelo menos o valor da minha aposta inicial antes do final da rodada. O craps é a solução... ou existe algum jogo de cartas melhor? Obrigado pelo seu tempo e esforço.
Obrigado. Se seu objetivo é ganhar apenas uma unidade, concordo que o craps é o melhor lugar para começar. A opção "don't pass" é ligeiramente melhor que a opção "pass". No entanto, se você perder sua primeira aposta, eu mudaria para o blackjack. Só voltaria para o craps se você estivesse exatamente no mesmo ponto de partida. Isso porque você não precisará dobrar ou dividir para ganhar apenas uma unidade, e um jogo de blackjack com apenas "hit/stand" tem uma vantagem da casa de cerca de 2,5%.
Fico muito feliz em ver que você voltou a mudar o mundo, um leitor com dificuldades em matemática de cada vez. Tenho uma pergunta que mistura um desabafo com uma questão de probabilidades. Vamos lá: um colega meu passou a vida inteira jogando blackjack e se irritando com o jogador que está na terceira base sempre que ele não segue a estratégia básica. Ele insiste que esse jogador "ruim" está prejudicando suas chances. Tenho 100% de certeza de que isso não altera as probabilidades em nada. Tentei explicar a ele que o motivo pelo qual ele acha que isso o prejudica é porque as vezes em que realmente o prejudicou ficam gravadas na memória, e ele provavelmente nem presta atenção às vezes em que o ajudou. Eu disse a ele que, matematicamente, as probabilidades dele são exatamente as mesmas, quer ele jogue em uma mesa com pessoas que nunca pedem carta, em uma mesa com pessoas que nunca param ou em uma mesa com pessoas que jogam a estratégia básica perfeita. Ele não acredita. Mas, como posso convencê-lo de que ele está errado? Devo continuar tentando? Se ele admitir que está errado, terá que admitir que repreendeu injustamente inúmeras pessoas nas mesas de blackjack, quando essas pessoas não estavam prejudicando ninguém além de si mesmas (e, em alguns casos, se estivessem contando cartas e ajustando suas estratégias de acordo, nem mesmo a si mesmas). Você não acha que os cassinos seriam lugares melhores se as pessoas realmente entendessem que o que eu faço com a minha mão de blackjack não altera as suas chances a longo prazo?
Seu colega parece um caso perdido. Como já disse antes, quanto mais ridícula uma ideia, mais tenazmente ela tende a ser mantida. Eu desistiria dele e o deixaria acreditar em sua ilusão. Pessoalmente, não dou conselhos sobre jogos de azar sem que me peçam, porque raramente são bem recebidos.
Eu tinha um blackjack e o crupiê me pagou. No final da rodada, ele virou as cartas e descobriu que também tinha um blackjack. Ele se esqueceu de conferir a mão antes de me pagar. Os supervisores queriam que eu devolvesse os ganhos. Eu me recusei. Parece que me lembro de um cenário semelhante de um livro sobre blackjack. Eu estava certo?
Eu digo que você deveria ter devolvido os ganhos. Nunca vi isso abordado em nenhum livro. No entanto, será que um livro é realmente necessário? É para isso que você tem a consciência. Pediram que você corrigisse as coisas, e é a coisa certa a fazer.
Adoro seu site! Acabei de encontrar sua lista detalhada das mesas de Blackjack de Las Vegas e suas respectivas vantagens, então fiquei com uma dúvida: suponha que existam duas mesas de Blackjack, uma com vantagem de 0,2% e aposta mínima de $10, e outra com vantagem de 0,4% e aposta mínima de $5. Ambas as mesas têm a mesma perda de $0,02 por mão. Existe alguma vantagem em escolher uma mesa em vez da outra?
Obrigado. Para responder a essa pergunta, você primeiro precisa se perguntar por que está jogando. Se você está tentando perder o mínimo possível, então não deveria jogar. No entanto, se você está jogando por diversão, eu escolheria o jogo de $10 com a vantagem de 0,2%. A perda esperada será a mesma, mas você terá uma experiência mais emocionante com apostas maiores.
Meus amigos e eu estamos planejando uma viagem de fim de semana para Las Vegas. Como estudante universitário, decidi que o máximo que posso me dar ao luxo de perder (acho que essa é a melhor maneira de definir um limite ao jogar) é US$ 500. Gostaria de saber quais jogos vocês acham que eu deveria jogar? E quais seriam os valores das apostas? Pode-se dizer que sou um pouco aventureiro, porque adoraria voltar para Durham com uma boa quantia e estou mentalmente preparado para perder tudo. Muito obrigado, seu site é fantástico.
Obrigado pelas palavras gentis. Os três jogos em que você pode obter uma vantagem da casa inferior a 0,5% são blackjack, craps e video poker. Dos três, eu recomendaria blackjack. Eu começaria apostando US$ 10 por mão. Jogando de forma conservadora no início, você não perderá todo o seu dinheiro tão cedo e não precisará pedir dinheiro emprestado aos seus amigos. Digamos que você queira dobrar seu saldo ou perder tudo tentando, então aumente suas apostas à medida que se aproxima do final da sua viagem. Certifique-se de memorizar a estratégia básica antes de jogar e não aceite nada além de uma vantagem da casa de 0,4%.
De quanto aumentaria a vantagem da casa se o jogador fizesse um seguro todas as vezes no blackjack?
O dealer terá um ás à mostra 1/13 das vezes. A vantagem da casa no seguro é de 7,395% em um jogo com seis baralhos, em média. No entanto, isso se aplica a metade do valor da aposta. Portanto, a perda esperada ao sempre fazer o seguro é (1/13) × 7,395% × 0,5 = -0,00284. Assim, a vantagem da casa aumentaria em 0,284%.
Para jogadores recreativos de blackjack que usam a estratégia básica e não contam cartas, a vantagem da casa aumenta conforme a penetração no baralho aumenta? Acredito que sim, porque quanto mais fundo se chega no baralho, maior tende a ser o valor absoluto da contagem, o que deveria desencadear mudanças na estratégia baseadas na contagem. Como o jogador que não conta cartas não saberia quando e como fazer essas mudanças, ele cometeria mais erros à medida que a contagem se afastasse de zero. Portanto, não seria melhor para um jogador que não conta cartas jogar em uma mesa com penetração rasa?
Em um jogo sem cartas de corte, a vantagem da casa é sempre a mesma para quem não conta as cartas. Grupos de cartas altas ou baixas têm a mesma probabilidade de aparecer no início, no meio ou no fim do baralho. O fato de a contagem ser zero no topo do baralho não significa que haverá um equilíbrio exato entre cartas altas e baixas. Você parece estar sugerindo que as cartas estão mais agrupadas no final do baralho. No entanto, se isso fosse verdade, as probabilidades mudariam se o crupiê distribuísse as cartas em ordem inversa. Certamente, essa é uma ideia absurda.
Digamos que o jogador com estratégia básica tenha 16 contra 10 no final do jogo e peça carta. Se a contagem fosse alta, ficar parado seria a jogada correta, o que pareceria um erro para um contador que estivesse observando. No entanto, se a contagem fosse negativa, pedir carta seria ainda melhor. No final, a média se equilibra para o jogador com estratégia básica.
Pelos motivos que explico no meu apêndice 10 sobre blackjack , o jogador que utiliza a estratégia básica deve preferir um jogo com embaralhador contínuo, caso seu objetivo seja minimizar a vantagem da casa. Além disso, a vantagem da casa não é afetada pela penetração. Devo acrescentar que, com uma penetração menor, haverá mais tempo gasto embaralhando as cartas e, portanto, uma perda esperada menor por hora.
Qual a sua opinião sobre o futuro do blackjack?
Vamos analisar os dados primeiro. A tabela a seguir mostra o número de mesas por jogo e ano no Condado de Clark, com base nos Relatórios Estatísticos Trimestrais do Departamento de Controle de Jogos de Nevada. Todos os anos são referentes ao quarto trimestre, exceto 2009, que é referente ao terceiro trimestre, pois, na data desta publicação, os dados do quarto trimestre ainda não estavam disponíveis. Esportes, corridas, bingo e keno não estão incluídos.
Total de jogos de mesa entre 1990 e 1999
| Jogo | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
|---|---|---|---|---|---|---|---|---|---|---|
| 21 | 2132 | 2094 | 1954 | 2132 | 2140 | 2134 | 2345 | 2383 | 2404 | 2664 |
| Roleta | 197 | 202 | 203 | 232 | 252 | 258 | 287 | 303 | 311 | 354 |
| Dados | 290 | 284 | 272 | 286 | 303 | 308 | 325 | 334 | 344 | 372 |
| Outros jogos | 3 | 5 | 8 | 28 | 95 | 15 | 25 | 51 | 56 | 71 |
| Bacará | 54 | 57 | 49 | 51 | 64 | 70 | 72 | 81 | 83 | 103 |
| Pai gow poker | 73 | 98 | 99 | 107 | 101 | 95 | 109 | 120 | 139 | 170 |
| pôquer de três cartas | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mini bacará | 26 | 33 | 39 | 40 | 43 | 51 | 73 | 77 | 85 | 94 |
| Deixe-o andar | 0 | 0 | 0 | 0 | 23 | 148 | 144 | 110 | 108 | 118 |
| Pai gow | 26 | 22 | 19 | 19 | 2 | 23 | 22 | 36 | 42 | 33 |
| Roda da fortuna | 47 | 44 | 42 | 39 | 48 | 46 | 37 | 34 | 34 | 36 |
| Caribbean Stud | 0 | 2 | 13 | 95 | 127 | 120 | 109 | 100 | 95 | 94 |
| Dê uma chance a Chuck | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 3 | 2 | 2 |
| Sic bo | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 |
| Craps sem merda | 3 | 3 | 1 | 1 | 6 | 4 | 2 | 1 | 0 | 0 |
| Meios Duplos | 3 | 3 | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| Nove para cima | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mais de 7 anos | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mais de 13 anos e menos de 13 anos | 3 | 11 | 12 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| Cachorro Vermelho | 13 | 14 | 17 | 10 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mesa de pôquer P&M | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Super panela nove | 4 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Total | 2883 | 2878 | 2734 | 3048 | 3207 | 3275 | 3554 | 3636 | 3706 | 4114 |
Total de jogos de mesa entre 2000 e 2009
| Jogo | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
|---|---|---|---|---|---|---|---|---|---|---|
| 21 | 2659 | 2605 | 2546 | 2561 | 2508 | 2662 | 2589 | 2528 | 2537 | 2448 |
| Roleta | 359 | 362 | 352 | 360 | 360 | 392 | 394 | 393 | 405 | 407 |
| Dados | 372 | 370 | 352 | 352 | 338 | 364 | 351 | 340 | 334 | 336 |
| Outros jogos | 101 | 143 | 52 | 68 | 81 | 121 | 196 | 283 | 243 | 226 |
| Bacará | 106 | 98 | 93 | 109 | 115 | 133 | 175 | 176 | 233 | 218 |
| Pai gow poker | 179 | 198 | 207 | 217 | 211 | 192 | 192 | 175 | 194 | 216 |
| pôquer de três cartas | 0 | 3 | 105 | 135 | 160 | 182 | 185 | 191 | 208 | 197 |
| Mini bacará | 110 | 118 | 126 | 115 | 124 | 147 | 148 | 130 | 143 | 140 |
| Deixe-o andar | 129 | 132 | 121 | 112 | 105 | 109 | 97 | 94 | 98 | 97 |
| Livro de corridas | 81 | 83 | 80 | 78 | 83 | 86 | 84 | 81 | 82 | 67 |
| Pai gow | 43 | 41 | 40 | 43 | 49 | 73 | 76 | 82 | 80 | 58 |
| Roda da fortuna | 41 | 42 | 41 | 40 | 40 | 37 | 37 | 33 | 37 | 40 |
| Caribbean Stud | 88 | 80 | 75 | 69 | 56 | 45 | 30 | 23 | 22 | 17 |
| Dê uma chance a Chuck | 2 | 1 | 2 | 2 | 3 | 1 | 1 | 1 | 1 | 1 |
| Sic bo | 3 | 6 | 6 | 4 | 2 | 1 | 2 | 1 | 1 | 1 |
| Craps sem merda | 0 | 1 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| Meios Duplos | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Nove para cima | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mais de 7 anos | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mais de 13 anos e menos de 13 anos | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Cachorro Vermelho | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mesa de pôquer P&M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Super panela nove | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total | 4192 | 4200 | 4120 | 4187 | 4154 | 4459 | 4473 | 4450 | 4536 | 4402 |
A próxima tabela mostra a porcentagem do mercado total de jogos de mesa para cada jogo em 1990 e 2009. Observe como o 21 foi o que mais perdeu participação de mercado, caindo de 74,0% para 55,6%.
Comparação de participação de mercado
| Jogo | 1990 | 2009 |
|---|---|---|
| 21 | 74,0% | 55,6% |
| Roleta | 6,8% | 9,2% |
| Dados | 10,1% | 7,6% |
| Outros jogos | 0,1% | 5,1% |
| Bacará | 1,9% | 5,0% |
| Pai gow poker | 2,5% | 4,9% |
| pôquer de três cartas | 0,0% | 4,5% |
| Mini bacará | 0,9% | 3,2% |
| Deixe-o andar | 0,0% | 2,2% |
| Pai gow | 0,9% | 1,3% |
| Roda da fortuna | 1,6% | 0,9% |
| Caribbean Stud | 0,0% | 0,4% |
| Dê uma chance a Chuck | 0,0% | 0,0% |
| Sic bo | 0,1% | 0,0% |
| Craps sem merda | 0,1% | 0,0% |
| Meios Duplos | 0,1% | 0,0% |
| Nove para cima | 0,1% | 0,0% |
| Mais de 7 anos | 0,0% | 0,0% |
| Mais de 13 anos e menos de 13 anos | 0,1% | 0,0% |
| Cachorro Vermelho | 0,5% | 0,0% |
| Mesa de pôquer P&M | 0,1% | 0,0% |
| Super panela nove | 0,1% | 0,0% |
Isso levanta a questão de por que o blackjack está perdendo participação de mercado. Aqui estão o que eu considero os principais motivos:
- A popularidade dos jogos baseados no pôquer está fazendo com que alguns jogadores mudem de modalidade.
- Os cassinos não oferecem bônus para jogos de blackjack tão bem quanto para outros jogos.
- As regras estão ficando mais complicadas. Não estou sugerindo que a maioria dos jogadores saiba disso, mas com o tempo, os jogadores podem sentir as mudanças nas regras, como o dealer pedir carta com um 17 suave, no bolso.
- Todos os jogos de cassino têm um ciclo de vida natural, e o blackjack está ficando cada vez mais antigo.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Alguns jogos de blackjack da Playtech têm a regra "Charlie das dez cartas". Qual é o valor disso?
Para benefício dos demais leitores, a regra do "Charlie das dez cartas" significa que, se o jogador conseguir chegar a dez cartas sem estourar, ele ganha automaticamente.
De acordo com minha simulação, a probabilidade de o jogador conseguir pelo menos dez cartas é de 1 em 60 milhões. Portanto, isso reduz a vantagem da casa em cerca de 0,0000017%.
No cassino Spielbank Bad Homburg , perto de Frankfurt, na Alemanha, existe uma carta especial no jogo de blackjack. Essa carta é um ás e substitui um dos ases comuns em um sapato de seis baralhos. A carta apresenta a imagem do fundador do cassino, François Blanc. Se o jogador conseguir um blackjack com essa carta, o pagamento é de 3 para 1, em vez do usual 3 para 2. É uma vitória automática para o jogador, mas um blackjack comum para o crupiê. São usados seis baralhos. Como essa regra afeta a vantagem da casa?
Demonstro que o valor combinado dessas regras é de 0,31%.
As regras do blackjack que eles seguem, e que parecem ser padrão em todos os cassinos Spielbank, são:
- Seis baralhos.
- O revendedor está em cima da linha macia de 17.
- Sem carta oculta do dealer.
- Oferta dupla apenas das 9h às 11h.
- Dobrar após dividir é permitido.
- Divida novamente qualquer par, incluindo ases, em até quatro mãos.
- Sem rendição.
- Embaralhador contínuo.
Usando minha calculadora de vantagem da casa no blackjack , obtive uma vantagem da casa de 0,55% antes da regra da carta François Blanc. A regra da carta François Blanc reduz a vantagem da casa para 0,24%!
De acordo com o regulamento do Spielbank Bad Homburg, o jogo François Blanc é exclusivo deste cassino.
Para saber como jogar de acordo com essas regras, visite minha estratégia básica europeia .
Qual é a vantagem da casa neste conjunto terrível de regras de blackjack, conhecido como "Party Blackjack" no cassino de Adelaide?
- Seis decks
- O revendedor acerta um 17 suave
- Sem carta fechada do dealer. O jogador perde o valor total da aposta se o dealer fizer um blackjack.
- Oferta dupla apenas das 9h às 11h.
- Dobrar após dividir é permitido.
- O jogador pode dividir novamente as cartas em três mãos, exceto ases.
- O Blackjack paga 6 para 5.
- Pressione o botão do revendedor 22.
Ai! Essas regras são tão ruins que me arrepiei só de lê-las.
Usando minha calculadora de vantagem da casa no blackjack , cheguei a uma vantagem de 2,22% antes de considerar as regras de não revelar a carta fechada e de empate (push 22). Estou assumindo que um embaralhador contínuo é usado e que o jogador pode dividir as cartas em quatro mãos. A regra de não revelar a carta fechada custa ao jogador mais 0,11%. No entanto, a regra mais prejudicial é o empate (push 22), que custa ao jogador 6,91%. O resultado final é uma vantagem da casa de 9,24%! Isso é simplesmente uma aberração para o jogo.
Convido meus leitores a me informarem se existe algum conjunto de regras de blackjack pior por aí.
O Harrah's na Filadélfia está pagando os seguintes bônus no blackjack:
Promoção do Harrah's Philadelphia
| Mão | Paga |
|---|---|
| Sete triplos | $ 500 |
| 21 de cinco cartas | $ 250 |
| Ás preto e blackjack | $ 150 |
| Ás vermelho e valete preto | $ 100 |
| blackjack de terno | $ 50 |
Para obter os bônus, é necessário apostar no mínimo $25. São utilizados seis baralhos. Você poderia me informar o valor desta promoção?
Ótima promoção! A tabela a seguir mostra a probabilidade de cada evento. A probabilidade de um 21 com cinco cartas deve ser considerada um pouco aproximada.
Análise de promoção do Harrah's Philadelphia
| Mão | Paga | Probabilidade | Retornar |
|---|---|---|---|
| Sete triplos | $ 500 | 0,000384552 | $ 0,19 |
| 21 de cinco cartas | $ 250 | 0,00453345 | $ 1,13 |
| Ás preto e blackjack | $ 150 | 0,002968093 | $ 0,45 |
| Ás vermelho e valete preto | $ 100 | 0,002968093 | $ 0,30 |
| blackjack de terno | $ 50 | 0,011872372 | $ 0,59 |
| Total | $- | 0,011872372 | $ 2,66 |
A célula inferior direita mostra que os bônus valem US$ 2,66 por mão jogada.
As regras do blackjack são bastante flexíveis, com uma vantagem da casa de apenas 0,35%. Com a aposta mínima exigida de US$ 25, a perda esperada por mão é de US$ 0,08. Portanto, a promoção vale US$ 2,57 por mão jogada.
Infelizmente, a promoção já terminou na data desta publicação.
Essa questão foi levantada e discutida no meu fórum no Wizard of Vegas .
Eu conheço uma máquina de blackjack onde, devido a um bug, o jogador pode recuperar uma aposta de seguro perdida. As regras são: oito baralhos, blackjack paga 3 para 2, o dealer pede carta com 17 suave, é permitido dobrar após dividir, não é permitido desistir e não é permitido dividir novamente. Qual é a vantagem da casa neste jogo se eu recuperar todas as apostas de seguro perdidas?
Esse bug equivale a receber uma unidade extra sempre que o dealer tiver um blackjack com um ás aberto. Isso acontecerá em 2,37% das vezes. A vantagem da casa seria de 0,72% sem esse bug. Com ele, a vantagem do jogador é de 2,37% - 0,72% = 1,66%.
Para mais informações sobre este assunto, consulte meu fórum no Wizard of Vegas .
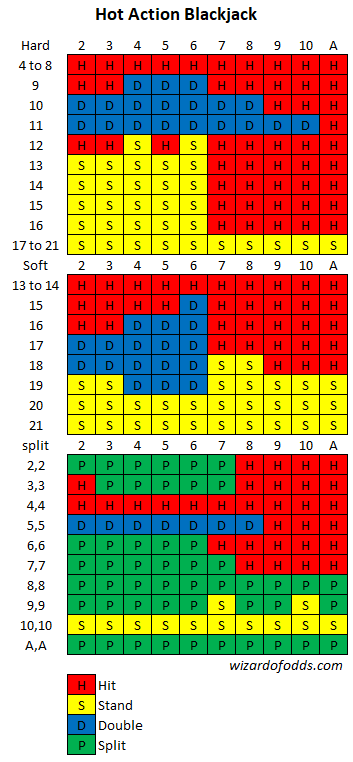
Existe um jogo de blackjack chamado Hot Action Blackjack sendo jogado no California Grand Casino em São Francisco. As regras do jogo são as seguintes:
- Seis baralhos em um embaralhador contínuo com 18 curingas adicionais com valor facial de 2.
- O revendedor atinge o nível 17 com relativa suavidade.
- Dobre o valor das suas duas primeiras cartas.
- Divida novamente até quatro mãos.
- Não é permitido trocar ou dividir ases novamente.
- Sem rendição.
- O Blackjack paga 6 para 5.
- Se as duas primeiras cartas do jogador forem curingas, ele recebe um bônus de 4 para 1.
- Se as duas primeiras cartas do jogador forem ases do mesmo naipe, ele recebe um bônus de 5 para 1.
- O jogador deve pagar uma comissão de 5% para jogar.
Qual é a estratégia básica e a vantagem da casa?
Primeiramente, aqui está minha estratégia básica de acordo com essas regras:
Considerando tudo, mostro uma vantagem da casa de 6,01% (ai!) com base na aposta inicial. Em outras palavras, se o jogador apostar US$ 100, sem contar a comissão de US$ 5, ele pode esperar perder US$ 6,01. Isso mostra por que eu evitaria jogos com banca de jogadores na Califórnia, a menos que você seja o banqueiro.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Vi as seguintes regras em uma máquina de blackjack de balcão no Binion's em Las Vegas: um baralho, o dealer para no 17 suave, o blackjack paga o dobro da aposta, tanto o jogador quanto o dealer devem parar com seis cartas, e não é permitido dobrar ou dividir. Qual é a vantagem da casa com esse conjunto de regras horrível?
Ai! Segundo Norm Wattenberger, criador do software de blackjack Casino Vérité , a vantagem da casa com essas regras é de 4,30%. Isso não leva em consideração a regra de parar com seis cartas, que, acredito, prejudica os dois lados de forma semelhante. Infelizmente, outros bares também têm esse mesmo conjunto de regras terríveis.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Encontrei uma máquina de blackjack com uma vantagem para o jogador de 0,1%. Em grupo, jogamos 2.015.000 mãos com apostas fixas e estamos com um prejuízo de 1.475 unidades. Não vou especificar as regras exatas para não revelar o jogo, então, por favor, considere a vantagem de 0,1% como válida. Quais são as chances de termos uma sequência de derrotas tão ruim, supondo que o jogo seja justo?
Com base nessa vantagem e nas mãos jogadas, o ganho esperado é de 2015 unidades. Assumindo um desvio padrão de 1,1 por mão, o desvio padrão em toda a jogada é de 1561. A diferença entre seu ganho real e o ganho esperado é de 3490. Isso é 3490/1561 = 2,24 desvios padrão. A probabilidade de resultados tão ruins ou piores é de 1,27%.
Encontrei uma máquina de blackjack com uma vantagem para o jogador de 0,1%. Em grupo, jogamos 2.015.000 mãos com apostas fixas e estamos com um prejuízo de 1.475 unidades. Não vou especificar as regras exatas para não revelar o jogo, então, por favor, considere a vantagem de 0,1% como válida. Quais são as chances de termos uma sequência de derrotas tão ruim, supondo que o jogo seja justo?
Com base nessa vantagem e nas mãos jogadas, o ganho esperado é de 2015 unidades. Assumindo um desvio padrão de 1,1 por mão, o desvio padrão em toda a jogada é de 1561. A diferença entre seu ganho real e o ganho esperado é de 3490. Isso é 3490/1561 = 2,24 desvios padrão. A probabilidade de resultados tão ruins ou piores é de 1,27%.
Olá, mago. Em 100.000 mãos de blackjack, quantas sequências de derrotas de 10 mãos ou mais posso esperar?
Primeiro, precisamos encontrar a probabilidade de vitória para qualquer mão específica, que dependerá das regras, as quais não foram mencionadas na sua pergunta original. Na minha página sobre variância no blackjack , apresento a probabilidade de vitória líquida, empate e derrota sob as "regras liberais do Strip", que são: seis baralhos, blackjack paga 3 para 2, o dealer para no 17 suave, dobrar após dividir permitido, desistir permitido, dividir ases novamente permitido. Sob essas regras, aqui estão as probabilidades necessárias:
- Vitória: 42,43%
- Empurrão: 8,48%
- Perda: 49,09%
Sua pergunta também não especificou como lidar com os empates. Vou assumir que um empate conta como uma mão jogada, mas não avança nem reinicia uma sequência de derrotas. Excluindo os empates, a probabilidade de uma vitória e de uma derrota, dada uma aposta resolvida, é:
- Vitória: 46,36%
- Perda: 53,64%
Dito isso, uma aproximação muito boa para perguntas como essa é:
n × l × w m
Onde:
n = número de mãos jogadas
l = probabilidade de uma perda
w = probabilidade de uma vitória
m = número mínimo de mãos em uma sequência de derrotas
Neste caso, o número esperado de perdas é 100000 × 46,36% × 63,64% × 10 = 91,4. Em outras palavras, haverá uma sequência de pelo menos 10 mãos perdidas a cada 1.094 mãos, em média. Uma simulação aleatória confirma isso.
Neste ponto, tenho certeza de que meus leitores perfeccionistas estão se preparando para me enviar e-mails com críticas intelectuais sobre cadeias de Markov . Gostaria de enfatizar que minha fórmula é uma ESTIMATIVA e, na verdade, uma estimativa bastante precisa.
Olá. Tenho um cupom que me permite fazer uma mão de 22. Posso guardar o cupom até conseguir a minha primeira mão de 22. Ele não se aplica a combinações duplas ou divididas. Qual é o valor disso?
Uma resposta rápida é o valor da aposta máxima permitida. Basta esperar por um 22 e então jogar, resultando em sair da mesa com uma unidade extra.
Uma resposta mais rigorosa deveria levar em conta o custo de esperar por esse 22. Isso é algo que eu não sei exatamente, mas posso estimar.
O custo para o jogador da regra de empate do dealer no 22 é de 6,91%. No entanto, o dealer chegará a 22 mais vezes do que isso, porque o jogador não se importará se estourar primeiro. Dependendo das regras, o jogador estourará cerca de 15,7% das vezes. Se assumirmos que isso não está correlacionado com a probabilidade de o dealer estourar (o que não está), então a probabilidade de o dealer estourar é de 6,91%/(1,0-0,157) = 8,2%.
Sei que é uma estimativa aproximada, mas vamos assumir que a probabilidade do jogador tirar 22 seja a mesma. Sei que o dealer vai estourar mais vezes do que o jogador, mas este cupom também não conta após uma divisão, então vamos considerar que esses fatores se compensam. Portanto, se o jogador tirar 22 em 8,2% das mãos, ele tirará 22 uma vez a cada 1/0,082 = 12,2 mãos em média.
Digamos que a vantagem da casa no jogo base seja de 0,75%. O custo de jogar 12,2 mãos com essa vantagem da casa é 12,2 * 0,0075 = 0,0915. Portanto, subtraindo isso do valor unitário, obtemos um valor para o cupom de 1,0 - 0,0915, que corresponde a cerca de 91% do valor nominal.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Estou pensando em criar uma aposta paralela para variantes de blackjack "push 22" que pagaria 11 para 1 se o dealer estourasse com 22. Quais seriam as probabilidades?
Estou pensando em criar uma aposta paralela para variantes de blackjack "push 22" que ganharia se o dealer ultrapassasse 22. Quais seriam as probabilidades de pagamento e qual seria a vantagem da casa?
Supondo que o dealer sempre compre todas as cartas da sua mão (mesmo que todos os jogadores já tenham estourado), então mostro uma probabilidade de estourar com 22 de 7,88% se o dealer parar no 17 suave e de 8,00% se ele pedir carta com um 17 suave.
Supondo que o dealer tire um 17 suave, com uma aposta de 11 para 1, a vantagem da casa seria de 4,04%. Com uma aposta de 10 para 1, essa vantagem sobe para 12,04%.
Devo avisá-los e orientar os jogadores de que isso seria contabilizado (cala a boca, Wiz!).
Encontrei um jogo de blackjack que paga 6 para 5 se o jogador fizer um blackjack depois de dividir dez ou ases? Dividir ases novamente não é permitido. Um blackjack do dealer ainda vence qualquer mão, exceto em caso de empate contra um blackjack natural do jogador. Se o dealer chegar a 21 pontos, um ás e um dez do jogador, após a divisão, vencem.
Vamos ignorar a divisão de dezenas, porque mesmo com essa regra, o jogador ainda deve parar no 20 contra qualquer coisa.
Considerando seis baralhos, a probabilidade de um par de ases é combin(24,2)/combin(312,2) = 276/48.516 = 0,5689%.
O número esperado de dois ases que se desenvolverão em um blackjack é 2*(16*6)/(312-2) = 0,619355.
A probabilidade de o dealer não ter um blackjack é 1 - (16*6)*(4*6-2)/combin(52*6-2,2) = 95,590354%.
A probabilidade do crupiê chegar a 21 pontos é de 7,7981%. O cálculo é muito complexo para explicar.
A probabilidade de a regra ser útil é 0,5689% * 95,590354% * (1-7,7981%) = 0,3368044%.
O benefício por incidente = Pr(o revendedor não atinge 21 pontos) * (0,2) + Pr(o revendedor atinge 21 pontos) * 1,2 = (1-0,122077839) * 0,2 + 0,122077839 * 1,2 = 0,3220778.
O benefício geral da regra é o produto da frequência com que a situação ocorre e o benefício quando ela ocorre = 0,003368044 * 0,322077839 = 0,11%.
O cassino Morongo , no sul da Califórnia, está com uma promoção em que paga um bônus de $16 se o crupiê receber um 16 rígido. Qual é o valor desse bônus?
Essa é uma boa opção para o jogador! O site deles não detalha as regras, então vou presumir que se aplica apenas às duas primeiras cartas. Vi em um antigo boletim informativo da Current Blackjack de outubro de 2018 que a maioria das mesas segue as seguintes regras:
- Concessionária atinge o nível 17
- Seis decks
- O Blackjack paga 3 para 2.
- Dobro após divisão permitido
- É permitido dividir ases novamente.
Minha calculadora de vantagem da casa no blackjack indica que essas regras têm uma vantagem da casa de 0,55% com um embaralhador contínuo e de 0,57% com uma carta de corte.
Independentemente das regras, a probabilidade de um 16 rígido nas duas primeiras cartas é de 6,51%. Receber $16 com uma probabilidade de 6,51% equivale a $1,04 por mão. Vou assumir uma aposta mínima de $25, pois a maioria dos cassinos está aumentando seus valores mínimos nesta era do coronavírus. Sem contar o bônus, a perda esperada por mão é de $0,14 com uma aposta de $25. Isso resulta em um ganho esperado por mão de $1,04 - $0,14 = $0,90. Em relação ao valor da aposta, isso representa uma vantagem para o jogador de 3,59%!
Se considerarmos um cenário ideal de jogar três mãos de $25 a 80 rodadas por hora, isso resultaria em um ganho esperado de $216 por hora!
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Em 12 horas de jogo de blackjack, qual é a probabilidade de se obter 60 ou mais vitórias consecutivas?
De acordo com a minha página sobre variância no blackjack , baseada nas regras liberais do Strip District, as probabilidades de um resultado líquido de vitória, empate ou derrota são as seguintes:
- Vitória — 42,43%
- Empurrão — 8,48%
- Perda — 49,09%
Vamos ignorar os empates, o que nos dá uma probabilidade de vitória, considerando que a mão resultou em um saldo positivo ou negativo, de 46,36%.
Vamos usar 100 mãos por hora como velocidade de jogo.
Podemos aproximar a probabilidade de ver pelo menos uma sequência de pelo menos 60 mãos consecutivas da seguinte forma:
100×12×0,4636 60 = 1 em 89.412.355.233.588.500.Para efeito de comparação, se você comprasse um bilhete da Powerball e um da Mega Millions, a probabilidade de ganhar em ambos seria de 1 em 88.412.922.115.818.300.
Portanto, seria um pouco mais provável ganhar nas duas loterias do que ter 60 vitórias consecutivas em 12 horas de jogo.
No filme "Licença para Matar", James Bond joga três rodadas de blackjack, jogando cinco mãos de cada vez. Percebi que ele nunca pediu carta em nenhuma delas. Qual a probabilidade disso?
Você pode encontrar um trecho da cena no YouTube .
O jogo apresenta um número suspeitamente alto de cartas grandes, não é? Aqui estão as cartas que consegui identificar. Observe que, em alguns casos, as cartas não estavam muito nítidas.
Licença para Matar -- Observações sobre as Fileiras
| Classificação | Observado |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| J | 3 |
| P | 6 |
| K | 4 |
| UM | 1 |
| Total | 35 |
Você tem toda razão, Bond não pede carta em nenhuma das suas 15 mãos iniciais. Ele divide um par de oitos uma vez, mas também não pede carta depois de dividir. Aqui está a contagem das suas ações iniciais em todas as 15 mãos:
- Duplo — 1
- Dividir — 1
- Posição — 13
Aqui estão as probabilidades básicas da estratégia para cada ação inicial, considerando seis baralhos, permissão para dobrar após dividir, o dealer espiar a carta fechada e o dealer parar no 17 suave.
Blackjack -- Probabilidades da Primeira Ação
| Ação | Probabilidade |
|---|---|
| Ficar | 43,46% |
| Bater | 39,78% |
| Dobro | 9,53% |
| Dividir | 2,48% |
| Blackjack | 4,75% |
| Total | 100,00% |
Caso a rendição fosse permitida, essa probabilidade seria de 4,14%, em comparação com a probabilidade de permanecer de pé.
Vale ressaltar que Bond já parou em 16 contra 10. A jogada básica da estratégia é pedir carta, mas a margem de sucesso é muito pequena. Dado o grande número de dez que apareceram naquela mão, Bond pode ter percebido que a contagem era alta, o que acionaria uma exceção à estratégia básica, permitindo que ele parasse naquela situação.
A probabilidade de não acertar nenhuma das 15 cartas é de 60,22%. A probabilidade de não acertar 15 das 15 cartas, assumindo que cada carta é independente, é de 0,602162 ÷ 15 = 0,000496253 ≈ 1 em 2015.
No cassino Golden Lion, na Cidade do Panamá, o crupiê oferece seguro com uma carta de 10 pontos. O pagamento é o mesmo, 2 para 1, tanto para um blackjack quanto para um ás. São usados seis baralhos. Qual é a vantagem da casa quando o crupiê tem um 10 à mostra?
Ai! Vi essa mesma regra horrível e ignorante no MGM em Macau.
A probabilidade de a carta fechada ser um ás com um 10 virado para cima é (6*4)/(6*52-1) = 7,717%. O retorno esperado é 0,077170×2 + 0,922830×-1 = -0,768489. Em outras palavras, a vantagem da casa é de 76,85%.
Vi que alguém no fórum afirma ter presenciado 60 mãos vencedoras consecutivas no blackjack. Quantas mãos seriam necessárias, em média, para presenciar isso? Além disso, como isso se compara ao evento mencionado na coluna 363 do Ask the Wizard , em que alguém alega ter presenciado 18 totais de 11 consecutivos no craps?
Para responder à sua pergunta, primeiro precisamos assumir algumas regras para o jogo de blackjack. Usarei o que chamo de "regras liberais de stripping", que são as seguintes:
- Seis decks
- O revendedor está em cima do 17 macio
- Dobro após divisão permitido
- É permitido dividir ases novamente.
- Rendição permitida
De acordo com essas regras, assumindo uma estratégia básica perfeita, estas são as probabilidades de um resultado líquido positivo/negativo:
- Lucro líquido: 42,43%
- Impulso líquido: 8,48%
- Prejuízo líquido: 49,09%
Interrogamos a testemunha do evento e ela disse que as 60 mãos não incluem empates. Em outras palavras, 60 mãos resolvidas. Também presumiremos que, se o jogador dividir, ainda conta como apenas uma mão e que houve um ganho líquido entre todas as mãos em que o jogador dividiu.
Conforme explicado na questão sobre os 18 totais consecutivos de 11, a fórmula para o tempo de espera esperado é:
Tempo de espera esperado = [(1/p)^(n+1) - 1] / [(1/p) - 1] - 1, onde:
n = número de vitórias consecutivas
p = probabilidade de vitória
Neste caso, a probabilidade de um ganho líquido por mão, dada uma mão resolvida, é de 42,43% / (43,43% + 49,09%) = 46,36%. Para ser mais específico, 0,46359564.
Usando a fórmula acima, o tempo de espera esperado para observar este evento é (1/0,46359564)^61 - 1]/[(1/0,46359564) - 1] - 1 = 200.941.772.393.648.000.000 mãos.
Em comparação, o tempo de espera para observar 18 totais de 11 em sequência no craps é de 41.660.902.667.961.000.000.000 lançamentos, ou seja, 207 vezes mais. Portanto, a história do rapaz de 18 anos ainda detém o recorde de maior exagero contado no fórum Wizard of Vegas, até onde eu sei.
Qual o valor de um cupom de ás grátis no blackjack 6-5?
Na minha página sobre o valor de um ás grátis , afirmo que seu valor é de 50,1844% do valor da aposta no blackjack 3-2.
No blackjack com seis baralhos, a probabilidade de obter um blackjack vencedor, com um ás como primeira carta, é de 29,3139%. Quando isso acontece, você ganha 0,3 unidades a menos no blackjack 6-5 do que no 3-2.
Assim, o valor de um ás grátis no blackjack 6-5 com seis baralhos é 50,1844% × 29,3139 × 0,3 = 41,3902% da aposta inicial.
Sua estratégia básica para seis baralhos, com o dealer parando em um 17 suave, é pedir carta com um 11 contra um ás. Qual seria a jogada correta se o jogador estivesse limitado a apenas uma carta caso optasse por pedir carta?
Minha calculadora de mãos de blackjack mostra que, com seis baralhos e o dealer parando no 17 suave, jogador 6+5 contra ás do dealer, os seguintes valores esperados para cada jogada são:
- Acerto = +0,147596
- Duplo = +0,129710
- Stand = -0,661883
Pedir carta, estando limitado a uma única carta, seria como dobrar a aposta, mas sem dobrar o valor apostado. O valor esperado seria, portanto, metade do valor esperado ao dobrar a aposta, ou +0,129710/2 = +0,064855. Isso é menor do que o valor esperado ao dobrar a aposta, que é +0,129710. Portanto, se você estiver limitado a uma única carta após pedir carta, então você deve dobrar a aposta.